30 câu Trắc nghiệm Chương 3: Hệ thức lượng trong tam giác (Kết nối tri thức 2023) có đáp án – Toán lớp 10

Trắc nghiệm Toán 10 Chương 3: Hệ thức lượng trong tam giác

I. Nhận biết

Câu 1. Khẳng định nào sau đây đúng ?

A. $co{s}^{2}x+si{n}^{2}x=1$;

B. $co{s}^{2}x+si{n}^{2}x=0$;

C. $co{s}^{2}x+si{n}^{2}x=2$;

D. $co{s}^{2}x+si{n}^{2}x=\frac{1}{4}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

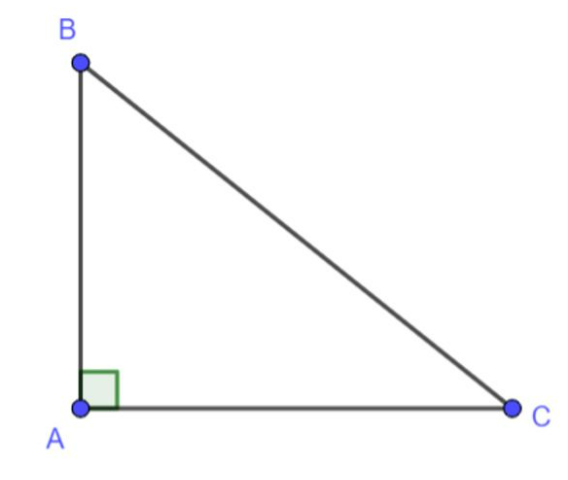
Giả sử  $\widehat{\text{ABC}}$= x.

Ta có cosx = $\frac{\text{AB}}{\text{BC}}$; sinx = $\frac{\text{AC}}{\text{BC}}$.

${\text{cos}}^{\text{2}}{\text{x\hspace{0.17em}+\hspace{0.17em}sin}}^{\text{2}}\text{x= }\frac{{\text{AB}}^2}{{\text{BC}}^2}\text{+}\frac{{\text{AC}}^2}{{\text{BC}}^2}\text{=}\frac{{\text{BC}}^2}{{\text{BC}}^2}\text{=1}$.

Câu 2. Cho tam giác ABC. Công thức nào sau đây sai?

A. $\frac{\text{b}}{\text{sinB}}=2\text{R}$;

B. $\frac{\text{a}}{\text{2sinA}}\text{ = R}$;

C. $\frac{\text{c}}{\text{sinC}}\text{ = 2R}$;

D. $\frac{\text{2c}}{\text{sinC}}\text{ = R}$.

Hướng dẫn giải

Đáp án: D

Giải thích:

Định lí sin: Trong tam giác ABC

$\frac{\text{a}}{\text{sinA}}\text{ = }\frac{\text{b}}{\text{sinB}}\text{ = }\frac{\text{c}}{\text{sinC}}\text{ = 2R}$.

Khẳng định A, B, C đúng. Khẳng định D sai.

Vậy chọn đáp án D.

Câu 3. Nội dung nào thể hiện công thức Heron?

A. S = $\sqrt{\text{2p(p + a)(p + b)(p + c)}}$;

B. S = $2\sqrt{\text{p(p }-\text{ a)(p }-\text{ b)(p }-\text{ c)}}$;

C. S = $\sqrt{\text{p(p + a)(p + b)(p + c)}}$;

D. S = $\sqrt{\text{p(p }-\text{ a)(p }-\text{ b)(p }-\text{ c)}}$.

Hướng dẫn giải

Đáp án: D

Giải thích:

Công thức Heron: S = $\sqrt{\text{p(p }-\text{ a)(p }-\text{ b)(p }-\text{ c)}}$.

Câu 4. Khẳng định nào sau đây đúng ?

A. sin( 180° – α ) = – sinα;

B. cos( 180° – α ) = cosα;

C. sin( 90° – α ) = – cosα;

D. cos( 90° – α ) = sinα.

Hướng dẫn giải

Đáp án: D

Giải thích:

Hai góc bù nhau có sin bằng nhau, côsin, tang, côtang đối nhau.

Khi đó ta có:

sin( 180° – α ) = sinα;

cos( 180° – α ) = – cosα.

Do đó A và B sai.

Hai góc phụ nhau có sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Khi đó ta có:

sin( 90° – α ) = cosα;

cos( 90° – α ) = sinα.

Do đó C sai và D đúng.

Câu 5. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Nội dung nào thể hiện định lí côsin?

A. $\frac{\text{a}}{\text{sinA}}\text{ = }\frac{\text{b}}{\text{sinB}}\text{ = }\frac{\text{c}}{\text{sinC}}$;

B. a² = b² + c² – 2bccosA;

C. S = $\frac{1}{2}$bcsinA = $\frac{1}{2}$acsinB = $\frac{1}{2}$absinC;

D. b² = a² + c² – 2bccosB .

Hướng dẫn giải

Đáp án: B

Giải thích:

Định lí côsin: Trong tam giác ABC

a² = b² + c² – 2bccosA

b² = a² + c² – 2accosB

c² = b² + a² – 2bacosC.

Vậy đáp án đúng là B.

Câu 6. M là điểm trên nửa đường trong lượng giác sao cho $\widehat{xOM}$= α. Tọa độ của điểm M là:

A. (sin α; cos α);

B. (cos α; sin α);

C. (– sin α; cos α);

D. ( – cos α; – sin α).

Hướng dẫn giải

Đáp án: B

Giải thích:

Định nghĩa tỉ số lượng giác của 1 góc bất kì từ 0° đến 180°:

Với góc α cho trước, 0° ≤ α ≤ 180°.

Gọi M(x₀;y₀) là điểm trên nửa đường tròn đơn vị nói trên sao cho $\widehat{xOM}$ = α. Ta có:

+ Sin của góc α là tung độ y₀  của điểm M kí hiệu là sinα.

+ Côsin của góc α là hoành độ x₀ của điểm M kí hiệu là cosα.

Câu 7. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Khẳng định nào dưới đây đúng?

A. a² = b² + c² + 2bcsinA;

B. a² = b² + c² – 2bccosA;

C. a² = b² + c² – 2acsinA;

D. a² = b² + c² + 2abcosA.

Hướng dẫn giải

Đáp án: B

Giải thích:

Định lí côsin:

Trong tam giác ABC: a² = b² + c² – 2bccosA.

Vậy đáp án đúng là B.

Câu 8. Khẳng định nào sau đây đúng ?

A. sin45° = $\frac{–\sqrt{2}}{2}$;

B. cos45° = 1;

C. tan45° = 1;

D. cot45° = $\frac{\sqrt{2}}{2}$.

Hướng dẫn giải

Đáp án: C

Giải thích:

Sử dụng máy tính cầm tay ta tính được:

sin45° = $\frac{\sqrt{2}}{2}$; cos45° = $\frac{\sqrt{2}}{2}$; tan45° = 1; cot45° = 1.

Do đó A, B, D sai và C đúng.

Câu 9. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Công thức tính diện tích nào dưới đây đúng?

A. S = $\frac{1}{2}$bcsinA;

B. S = $\frac{1}{2}$absinB;

C. S = 2acsinB;

D. S = 2bcsinA.

Hướng dẫn giải

Đáp án: A

Giải thích:

Công thức tính diện tích tam giác ABC: S = $\frac{1}{2}$bcsinA.

Câu 10. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Nội dung nào thể hiện định lí sin?

A. $\frac{\text{a}}{\text{sinA}}\text{ = }\frac{\text{b}}{\text{sinB}}\text{ = }\frac{\text{c}}{\text{sinC}}$;

B. a² = b² + c² – 2bccosA;

C. S = $\frac{1}{2}$bcsinA = $\frac{1}{2}$acsinB = $\frac{1}{2}$absinC;

D. b² = a² + c² – 2accosB .

Hướng dẫn giải

II. Thông hiểu

Câu 1. Cho tam giác ABC có a = 2, b = 5, c = 5. Tính bán kính đường tròn nội tiếp tam giác ABC.

A. 1;

B. $\sqrt{6}$;

C. 0,5;

D. $\frac{\sqrt{6}}{3}$.

Hướng dẫn giải

Đáp án: D

Giải thích:

Ta có: p = $\frac{2+5+5}{2}$ = 6

Áp dụng công thức Heron:

S = $\sqrt{\text{p(p }-\text{ a)(p }-\text{ b)(p }-\text{ c)}}$.

S =$\sqrt{6.(6-2).(6-5).(6-5)}$

S = $2\sqrt{6}$.

Mà S = pr = 6r = $2\sqrt{6}$ ⇒ r = $\frac{\sqrt{6}}{3}$.

Vậy đáp án đúng là D.

Câu 2. Tính giá trị biểu thức P = sin30°.cos15° + sin150°.cos165°

A. 0;

B. 1;

C. – 1;

D. 0,5.

Hướng dẫn giải

Đáp án: A

Giải thích:

Sử dụng công thức: sin( 180° – α ) = sinα và cos( 180° – α ) = – cosα.

Có sin30° = sin150°; cos15° = – cos165°

P = sin30°.cos15° – sin30°.cos15°= 0.

Câu 3. Tam giác ABC có AB = $\frac{\sqrt{6}-\sqrt{2}}{2}$, BC = $\sqrt{3}$, CA = $\sqrt{2}$. Tính số đo góc A.

A. 60°;

B. 90°;

C. 120°;

D. 30°.

Hướng dẫn giải

Đáp án: C

Giải thích:

Đặt AB = c, BC = a, AC = b

Theo định lí côsin ta có: a² = b² + c² – 2bccosA

⇒ cosA = $\frac{{\text{b}}^2+{\text{c}}^2-{\text{a}}^2}{2\text{bc}}$

⇒ cosA = $\frac{{\left(\frac{\sqrt{6}-\sqrt{2}}{2}\right)}^2+2-3}{2.\frac{\sqrt{6}-\sqrt{2}}{2}.\sqrt{2}}$

⇒ cosA = $\frac{-1}{2}$

⇒ $\widehat{\text{A}}$ = 120°.

Vậy đáp án C đúng.

Câu 4. Tính giá trị biểu thức S = sin²35° + cos²25° + sin²55° + cos²65°.

A. 3;

B. 2;

C. 1;

D. 0.

Hướng dẫn giải

Đáp án: B

Giải thích:

Sử dụng: sin( 90° – α ) = cosα và cos( 90° – α ) = sinα     

S = sin²35° + cos²25° + sin²55° + cos²65°

⇔ S = sin²35° + cos²25° + [ sin(90° – 35°)]² + [ cos(90° – 25°)]²

⇔ S = sin²35° + cos²25° + cos²35° + sin²25°

⇔ S = ( sin²35° + cos²35° ) + ( cos²25° + sin²25° )

⇔ S = 2.

Câu 5. Tính diện tích tam giác ABC có b = 2,  $\widehat{\text{B}}$= 30°, $\widehat{\text{C}}$ = 45°.

A. 1 + $\sqrt{3}$;

B. 1 – $\sqrt{3}$;

C. $\frac{1+\sqrt{3}}{2}$;

D. $\frac{1–\sqrt{3}}{2}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

Xét tam giác ABC có: $\widehat{\text{A}}$ + $\widehat{\text{B}}$ + $\widehat{\text{C}}$ = 180° ⇒ $\widehat{\text{A}}$ = 180° – 30° – 45° = 105°.

Áp dụng định lí sin:  $\frac{\text{b}}{\text{sinB}}\text{ = }\frac{\text{c}}{\text{sinC}}$⇒ $\frac{\text{2}}{\text{sin30}°}=\frac{\text{c}}{\text{sin45}°}$ ⇒ c = $2\sqrt{2}$.

S = $\frac{1}{2}$bcsinA = $\frac{1}{2}$.2.$2\sqrt{2}$.sin105° = 1 + $\sqrt{3}$

Vậy đáp án A đúng.

Câu 6. Biểu thức P = tan15°.tan25°.tan35°.tan55°.tan65°.tan75° có giá trị bằng?

A. 2;

B. –1;

C. 1;

D. 0.

Hướng dẫn giải

Đáp án: C

Giải thích:

Sử dụng công thức: tan( 90° – α ) = cotα và $\text{tanα =}\frac{\text{1}}{\text{cotα}}$ hay tanα.cotα = 1

P = tan15°.tan25°.tan35°.tan55°.tan65°.tan75° 

⇔ P = tan15°.tan25°.tan35°.cot35°.cot25°.cot15°

⇔ P = (tan15°.cot15°)(tan25°.cot25°).(tan35°.cot35°)

⇔ P = 1.1.1

⇔ P = 1.

Câu 7. Cho tam giác ABC có BC = 8 và $\widehat{\text{A}}$= 30°. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

A. $\frac{8\sqrt{3}}{3}$;

B. $\frac{16\sqrt{3}}{3}$;

C. 16;

D. 8.

Hướng dẫn giải

Đáp án: D

Giải thích:

Áp dụng định lí sin trong tam giác ABC:

$\frac{\text{BC}}{\text{sinA}}$= 2R

R = $\frac{\text{BC}}{\text{2sinA}}$

R = $\frac{8}{2.\sin 30°}$

R = 8.

Vậy đáp án đúng là D.

Câu 8. Cho tam giác ABC có b = 8, c = 5 và  $\widehat{\mathrm{B}}$= 80°. Tính số đo góc C.

A. 37°98’;

B. 38°98’;

C. 37°59’;

D. 36°98’.

Hướng dẫn giải

Đáp án: C

Giải thích:

Áp dụng định lí sin: $\frac{\text{b}}{\text{sinB}}\text{ = }\frac{\text{c}}{\text{sinC}}$

 

⇒ $\frac{8}{\sin 80°}=\frac{5}{\sin \text{C}}$

⇒ sin C = 5 : $\frac{8}{\sin 80°}$

⇒  $\widehat{\text{C}}$≈ 37°59’

Vậy đáp án đúng là C.

Câu 9. Cho tam giác ABC có a = 3, b = 4, c = 5. Tính diện tích tam giác ABC.

A. $6\sqrt{2}$;

B. 6;

C. 12;

D. 8.

Hướng dẫn giải

Đáp án: B

Giải thích:

Ta có: p = $\frac{3+4+5}{2}$ = 6

Áp dụng công thức Heron:

S = $\sqrt{\text{p(p }-\text{ a)(p }-\text{ b)(p }-\text{ c)}}$.

S = $\sqrt{6.(6-3).(6-4).(6-5)}$

S = 6.

Vậy đáp án đúng là B.

Câu 10. Cho tam giác ABC. Tính P = sinA.cos(B + C) + sin(B + C).cosA

A. 0;

B. 1;

C. -1;

D. 0,5.

Hướng dẫn giải

Đáp án: A

Giải thích:

Giả sử: $\widehat{A}$ = α; $\widehat{B}+\widehat{C}=\beta$. Do $\widehat{A}$, $\widehat{B},\widehat{C}$ là 3 góc trong tam giác nên α + β = 180°

⇒ β = 180° – α

⇒ sinβ = sin(180° – α) = sinα và cosβ = cos( 180° – α ) = – cosα

P = sinA.cos(B + C) + sin(B + C).cosA = sinα.cosβ + sinβ.cos α = sinα.(–cosα) + sinα.cos α  = 0.

Câu 11. Cho tam giác ABC có  $\widehat{\text{B}}$= 120°, AB = 6, BC = 7. Tính AC.

A. $\sqrt{127}$;

B. $\sqrt{43}$;

C. 8;

D. $\sqrt{106}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

Áp dụng định lí côsin trong tam giác ABC:

AC² = AB² + BC² – 2AB.BC.cosB

AC² = 6² + 7² – 2.6.7.cos120°

AC² = 127

AC = $\sqrt{127}$

Vậy đáp án A đúng.

Câu 12. Cho P = ( sinα + cosβ)(sinα − cosβ) + (cosα + sinβ)(cosα − sinβ)

Giá trị của biểu thức P là?

A. 1;

B. 0;

C. 2;

D. 3.

Hướng dẫn giải

Đáp án: B

Giải thích:

P = ( sinα + cosβ)(sinα − cosβ) + (cosα + sinβ)(cosα − sinβ)

⇔ P = $si{n}^2\alpha –co{s}^2\beta +co{s}^2\alpha –si{n}^2\text{β}$

⇔ P = 0

Câu 13. Tính giá trị biểu thức A = cot20° + cot40° + cot60° + …. + cot160°

A. 1;

B. 2;

C. 0;

D. 4.

Hướng dẫn giải

Đáp án: C

Giải thích:

Sử dụng cot( 180° – α ) = – cotα với 0° < α < 180°

Hay cot( 180° – α ) + cotα = 0

A = ( cot20° + cot160°) + ( cot40° + cot140°) + ( cot60° + cot120°) + ( cot80° + cot100°)

⇔ A = 0.

Câu 14. Cho tam giác ABC có AB = 5, AC = 6, BC = 7. Tính cosB.

A. $\frac{11}{7}$;

B. $\frac{17}{35}$;

C. $\frac{19}{35}$;

D. $\frac{13}{7}$.

Hướng dẫn giải

Đáp án: C

Giải thích:

Áp dụng định lí côsin trong tam giác ABC, có:

AC² = AB² + BC² – 2AB.BC.cosB

6² = 5² + 7² – 2.5.7.cosB

cosB = $\frac{5^2+7^2-6^2}{\mathrm{2.5.7}}$

cosB = $\frac{19}{35}$

Vậy đáp án đúng là C.

Câu 15. Cho góc α biết sinα + cosα = $\frac{5}{4}$. Tính A = sinα.cosα

A. $\frac{9}{32}$;

B. $\frac{7}{32}$;

C. $\frac{2}{39}$;

D. $\frac{9}{37}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

${(\sin \alpha +\cos \alpha )}^2={\sin }^2\alpha +{\cos }^2\alpha +2\sin \alpha .\cos \alpha =1+2\sin \alpha \cos \alpha =\frac{25}{16}$

⇔ $sin\alpha .cos\alpha =\frac{\frac{25}{16}-1}{2}=\frac{9}{32}$.

III. Vận dụng

Câu 1. Tam giác ABC có BC = a, AC = b, AB = c. Các cạnh a, b, c liên hệ với nhau bằng đẳng thức b.( b² – a² ) = c.( a² – c² ). Tính $\widehat{\text{BAC}}$.

A. 120°;

B. 90°;

C. 30°;

D. 60°.

Hướng dẫn giải

Đáp án: D

Giải thích:

b.( b² – a² ) = c.( a² – c² )

⟺ b³ – a²b – a²c + c³ = 0

⟺ b³ + c³ – ( a²b + a²c ) = 0

⟺ ( b + c )( b² – bc + c² ) – a²( b + c ) = 0

⟺ ( b + c ) ( b² + c² – a² – bc ) = 0

b và c là cạnh tam giác nên b + c > 0

⇒ b² + c² – a² – bc = 0 hay a² = b² + c² – bc

Theo định lí côsin

a² = b² + c² – 2bccosA

mà a² = b² + c² – bc ⇒ cosA = $\frac{1}{2}$ ⇒ $\widehat{\text{BAC}}$ = 60°.

Vậy đáp án đúng là D.

Câu 2. Cho 3cosα – sinα = 1; 0° < α < 90°. Tính tanα.

A. $\frac{4}{3}$;

B. $\frac{3}{4}$;

C. $\frac{4}{5}$;

D. $\frac{5}{4}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

3cosα – sinα = 1

⇔ 3cosα = 1 + sinα

⇒ 9cos²α = (sinα + 1)²  = sin²α + 2.sin α +1

⇒ 9 – 9sin² α = sin²α + 2.sin α +1

⇒ 10 sin²α + 2.sinα – 8 = 0

⇒ sinα = – 1 hoặc sinα = $\frac{4}{5}$

Với sinα = – 1 không thỏa mãn

Với sinα = $\frac{4}{5}$ ⇒  cosα = $\frac{3}{5}$

Vậy tanα = $\frac{4}{3}$.

Câu 3. Trên nóc tòa nhà có một cột ăng – ten cao 5m. Từ vị trí quan sát A cao 7m so với mặt đất có thể quan sát được đỉnh B và chân C của cột ăng – ten dưới góc 50° và 40° so với phường nằm ngang. Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?

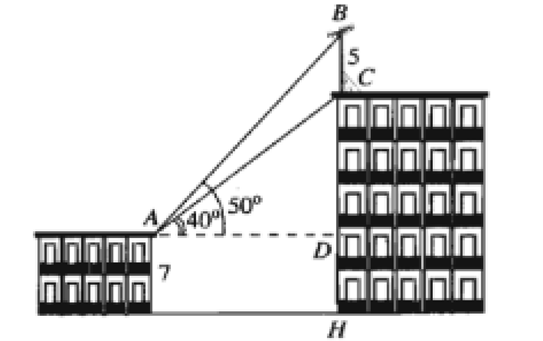
A. 12m;

B. 19m;

C. 29m;

D. 24m.

Hướng dẫn giải

Đáp án: B

Giải thích:

Gọi điểm H là chân tòa nhà. Điểm D là điểm tương ứng trên tòa nhà ngang bằng với vị trí quan sát A. Như vậy  $\widehat{\text{ADC}}$= 90°.

Từ vị trí quan sát A cao 7m so với mặt đất có thể quan sát được đỉnh B và chân C của cột ăng – ten dưới góc 50° và 40° so với phường nằm ngang. Như vậy $\widehat{\text{DAC}}$ = 40° và $\widehat{\text{DAB}}$ = 50°.

Xét tam giác ABD có:  $\widehat{\text{ABD}}$= 180 – $\widehat{\text{ADB}}$ – $\widehat{\text{DAB}}$ = 180° – 90° – 50° = 40° = $\widehat{\text{ABC}}$.

Xét tam giác ABC có:

$\widehat{\text{BAC}}$ = 50° – 40° = 10°.

Áp dụng định lí sin cho tam giác ABC:

$\frac{\text{BC}}{\sin \text{A}}=\frac{\text{AC}}{\sin \text{B}}$ ⇒ $\frac{5}{\sin 10°}=\frac{\text{AC}}{\sin 40°}$ ⇒ AC ≈ 18,5m

Áp dụng định lí sin cho tam giác ADC:

$\frac{\text{CD}}{\sin \text{A}}=\frac{\text{AC}}{\sin \text{D}}$ ⇒ $\frac{\text{CD}}{\sin 40°}=\frac{18,5}{\sin 90°}$ ⇒ CD ≈ 11,9m

Chiều cao tòa nhà tương ứng với đoạn CH.

CH = CD + DH =  11,9 + 7 = 18,9 ≈ 19m.

Vậy đáp án đúng là B.

Câu 4. Cho biết $2cos\alpha +\sqrt{2}sin\alpha =2$. Tính cotα biết 0° < α < 90°.

A. $\frac{\sqrt{5}}{4}$;

B. $\frac{\sqrt{3}}{4}$;

C. $\frac{\sqrt{2}}{4}$;

D. $\frac{\sqrt{2}}{2}$.

Hướng dẫn giải

Đáp án: C

Giải thích:

2cosα + $\sqrt{2}$sinα = 2 ⟺ $\sqrt{2}$sinα = 2 – 2cosα ⇒ 2sin²α = 4 – 8cos + 4 cos²α

⟹ 2 – 2cos²α = 4 – 8cosα + 4cos²α

⟹ 6cos² α – 8cosα + 2 = 0

cosα = 1 không thỏa mãn 0° < α < 90°.

cosα =$\frac{1}{3}$ ⇒ cotα= $\frac{\sqrt{2}}{4}$.

Câu 5. Hai chiếc tàu thủy cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60°. Tàu tới B chạy với tốc độ 20 hải lí một giờ. Tàu tới C chạy với tốc độ 15 hải lí một giờ. Hỏi sau hai giờ hai tàu cách nhau bao nhiêu hải lí? ( Chọn kết quả gần nhất ).

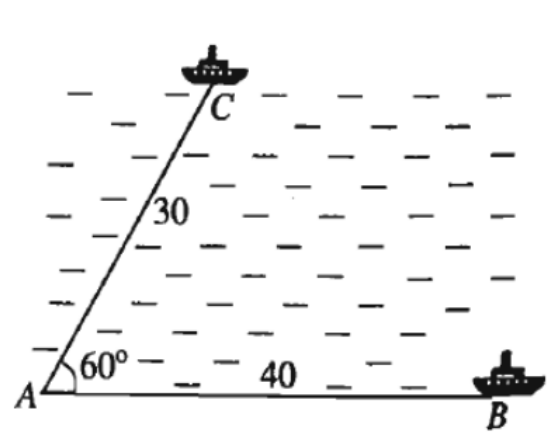
A. 61 hải lí;

B. 36 hải lí;

C. 18 hải lí;

D. 21 hải lí.

Hướng dẫn giải

Đáp án: B

Giải thích:

Sau 2h, tàu tới C đi được đoạn đường b = 15.2 = 30 ( hải lí )

Sau 2h, tàu tới B đi được đoạn đường c = 15.2 = 40 ( hải lí )

Dựa vào hình vẽ, sau 2h, tàu B và tàu C tạo với điểm xuất phát một tam giác ABC có

$\widehat{\text{A}}$= 60°, b = 30, c = 40 và a = BC.

Áp dụng định lí côsin ta có:

a² = b² + c² – 2bccosA

a² = 30² + 40² – 2.30.40.cos60°

a² = 1300

a ≈ 36 ( hải lí ).

Vậy đáp án đúng là B.

Xem thêm các bài trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Trắc nghiệm Bài 6: Hệ thức lượng trong tam giác

Trắc nghiệm Bài ôn tập cuối chương 3

Trắc nghiệm Toán 10 Bài 7: Các khái niệm mở đầu

Trắc nghiệm Toán 10 Bài 8: Tổng và hiệu của hai vectơ

Trắc nghiệm Toán 10 Bài 9: Tích của một vectơ với một số