Cho Hình 3.6. Biết tia Oz là tia phân giác của \(\widehat {xOy}\). Tính \(\widehat {xOy}\)

Câu hỏi:

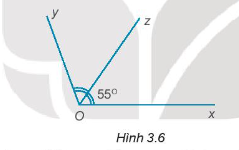
Cho Hình 3.6. Biết tia Oz là tia phân giác của \(\widehat {xOy}\). Tính \(\widehat {xOy}\)

Trả lời:

Lời giải:
Vì Oz là tia phân giác của góc \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{{\widehat {xOy}}}{2} = 55^\circ \).
Do đó, \(\widehat {xOy} = 55^\circ .2 = 110^\circ \).
Vậy \(\widehat {xOy} = 110^\circ \).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho Hình 3.4, kể tên các cặp góc kề bù.
   
   

   Câu hỏi:
   

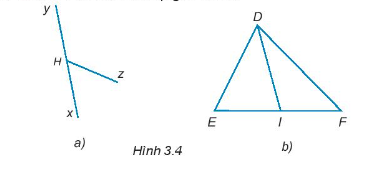
   Cho Hình 3.4, kể tên các cặp góc kề bù.
   

   Trả lời:

   Lời giải:
   Các cặp góc kề bù có trong hình là:
   Hình 3.4a: \(\widehat {xHz}\) và \(\widehat {yHz}\)
   Hình 3.4b: \(\widehat {EID}\) và \(\widehat {FID}\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho Hình 3.5 Gọi tên các cặp góc đối đỉnh.
   
   

   Câu hỏi:
   

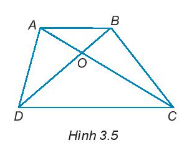
   Cho Hình 3.5
   
   Gọi tên các cặp góc đối đỉnh.

   Trả lời:

   Lời giải:
   Các cặp góc đối đỉnh là: \(\widehat {AOB}\) và \(\widehat {DOC}\); \(\widehat {AOD}\) và \(\widehat {BOC}\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Gọi tên góc kề bù với \(\widehat {AOD}\).
   
   

   Câu hỏi:
   

   Gọi tên góc kề bù với \(\widehat {AOD}\).

   Trả lời:

   Hướng dẫn giải:
   Góc kề bù với góc \(\widehat {AOD}\) là góc \(\widehat {AOB}\) và \(\widehat {COD}\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Vẽ hai đường thẳng xy và mn cắt nhau tại điểm O sao cho \(\widehat {xOm} = 120^\circ \). Tính các góc \(\widehat {mOy};\widehat {yOn};\widehat {xOn}\).
   
   

   Câu hỏi:
   

   Vẽ hai đường thẳng xy và mn cắt nhau tại điểm O sao cho \(\widehat {xOm} = 120^\circ \). Tính các góc \(\widehat {mOy};\widehat {yOn};\widehat {xOn}\).

   Trả lời:

   Lời giải:
   
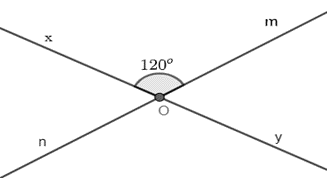
   Vì góc \(\widehat {xOm}\) và góc \(\widehat {nOy}\)là hai góc đối đỉnh nên \(\widehat {xOm}\) = \(\widehat {nOy} = 120^\circ \)
   Vì góc \(\widehat {xOn}\) và góc \(\widehat {xOm}\) là hai góc kề bù nên \(\widehat {xOn}\) + \(\widehat {xOm} = 180^\circ \)
   \(\widehat {xOn}\) + \(120^\circ = 180^\circ \)
   \(\widehat {xOn}\) = 180^o – 120^o
   \(\widehat {xOn}\) = 60^o.
   Mà \(\widehat {xOn}\) và \(\widehat {yOm}\) đối đỉnh nên \(\widehat {xOn}\) = \(\widehat {yOm}\) = 60^o.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Vẽ \(\widehat {xAm} = 50^\circ \). Vẽ tia phân giác An của \(\widehat {xAm}\). Tính \(\widehat {xAn}\).
   
   

   Câu hỏi:
   

   Vẽ \(\widehat {xAm} = 50^\circ \). Vẽ tia phân giác An của \(\widehat {xAm}\).
   Tính \(\widehat {xAn}\).

   Trả lời:

   Lời giải:
   
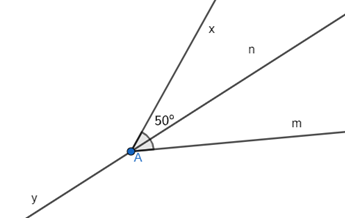
    Vì An là tia phân giác của góc \(\widehat {xAm}\) nên \(\widehat {xAn} = \widehat {mAn} = \frac{{\widehat {xAM}}}{2} = \frac{{50^\circ }}{2} = 25^\circ \).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====