Câu hỏi:
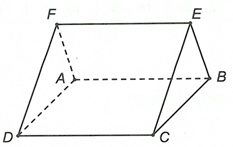
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Kết quả nào sau đây đúng?
A.
B.
Đáp án chính xác
C.
D.
Trả lời:
Đáp án B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tứ diện ABCD có M, N, P lần lượt là trọng tâm của ΔABC, ΔACD, ΔABD.
Chứng minh rằng MNP // BCD.
Câu hỏi:
Cho tứ diện ABCD có M, N, P lần lượt là trọng tâm của
Chứng minh rằngTrả lời:
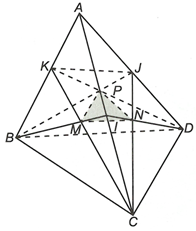
Gọi I, J, K lần lượt là trung điểm AC, AD, AB.
Xét có nên
Suy ra
Xét có nên
Suy ra
Ta có
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm SA, SB, SC.a) Chứng minh (MNP) // (ABCD)
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm SA, SB, SC.
a) Chứng minh (MNP) // (ABCD)Trả lời:
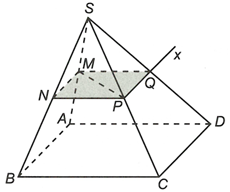
a) Ta có
Tương tự
Ta có====== **** mời các bạn xem câu tiếp bên dưới **** =====
- b) Gọi Q là giao điểm của (MNP) và SD. Chứng minh tứ giác MNPQ là hình bình hành.
Câu hỏi:
b) Gọi Q là giao điểm của (MNP) và SD. Chứng minh tứ giác MNPQ là hình bình hành.
Trả lời:
b) Ta có
Xét hai mặt phẳng và có
Ta có
sao cho (vì MN // AB theo tính chất đường trung bình và CD // AB)
Trong gọi Suy ra
Ta có nên suy ra Q là trung điểm của SD và
Vậy tứ giác MNPQ là hình bình hành (cặp cạnh đối song song và bằng nhau).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của A’B’ và AB. Chứng minh (AMC’) // (CNB’)
Câu hỏi:
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của A’B’ và AB. Chứng minh (AMC’) // (CNB’)
Trả lời:
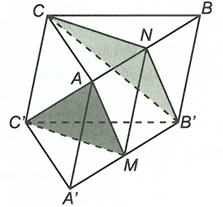
Ta có và theo tính chất hình lăng trụ thì nên tứ giác là hình bình hành và
Mặt khác nên tứ giác là hình bình hành và
Ta có
Lại có====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình lập phương ABCD.A’B’C’D’, có M, N, P lần lượt là trung điểm của các cạnh AD, DC, DD’. Chứng minh rằng (MNP) song song với (ACD’)
Câu hỏi:
Cho hình lập phương ABCD.A’B’C’D’, có M, N, P lần lượt là trung điểm của các cạnh AD, DC, DD’. Chứng minh rằng (MNP) song song với (ACD’)
Trả lời:
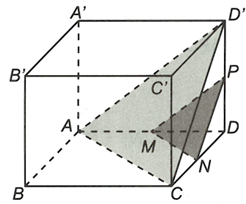
Xét có mà
Tương tự trong có mà
Ta có
Suy ra====== **** mời các bạn xem câu tiếp bên dưới **** =====