Câu hỏi:
Xét khai triển của
a) Xác định hệ số của x7.
b) Nêu số hạng tổng quát trong khai triển nhị thức trên, từ đó nêu hệ số ak của xk với 0 ≤ k ≤ 12.
Trả lời:
a) Số hạng chứa x7 là Hệ số của x7 là
b) Số hạng tổng quát trong khai triển trên là
Hệ số của xk là
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- a) Chọn số thích hợp cho ? trong khai triển biểu thức sau:
(a+b)3=C3?a3−?+C3?a3−?b1+C3?a3−?b2+C3?a3−?b3.
Từ đó nêu dạng tổng quát của mỗi số hạng trong khai triển biểu thức (a + b)3.
b) Xét biểu thức (a + b)n.
Nêu dự đoán về dạng tổng quát của mỗi số hạng trong khai triển biểu thức (a + b)n.
Câu hỏi:
a) Chọn số thích hợp cho ? trong khai triển biểu thức sau:
Từ đó nêu dạng tổng quát của mỗi số hạng trong khai triển biểu thức (a + b)3.
b) Xét biểu thức (a + b)n.
Nêu dự đoán về dạng tổng quát của mỗi số hạng trong khai triển biểu thức (a + b)n.Trả lời:
a)
Mỗi số hạng trong khai triển biểu thức (a + b)3 đều có dạng
b) Cũng như thế, mỗi số hạng trong khai triển
biểu thức (a + b)n đều có dạng====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Khai triển biểu thức (x + 2)7.
Câu hỏi:
Khai triển biểu thức (x + 2)7.
Trả lời:
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho n∈ℕ* . Chứng minh Cn0+Cn1+Cn2+…+Cnn−1+Cnn=2n.
Câu hỏi:
Cho . Chứng minh
Trả lời:
Ta có:
Cho x = 1, ta được:
Vậy====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Ta đã biết:
(a+b)2=C20a2+C21ab+C22b2;
(a+b)3=C30a3+C31a2b+C32ab2+C33b3;
(a+b)4=C40a4+C41a3b+C42a2b2+C43ab3+C44b4;
(a+b)5=C50a5+C51a4b+C52a3b2+C53a2b3+C54ab4+C55b5.
Ta sắp xểp những hệ số tổ hợp ở trên như sau:
Nêu phép toán để từ hai số hạng của dòng trên suy ra được số hạng tương ứng (thể hiện ở mũi tên ↓) ở dòng dưới trong bảng các hệ số nói trên.
Câu hỏi:
Ta đã biết:
Ta sắp xểp những hệ số tổ hợp ở trên như sau:
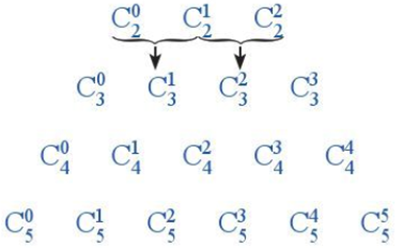
Nêu phép toán để từ hai số hạng của dòng trên suy ra được số hạng tương ứng (thể hiện ở mũi tên ↓) ở dòng dưới trong bảng các hệ số nói trên.
Trả lời:
Tổng của hai số hạng của dòng trên bằng số hạng tương ứng ở dòng dưới.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Sử dụng tam giác Pascal để khai triển:
a) (x + y)7;
b) (x – 2)7.
Câu hỏi:
Sử dụng tam giác Pascal để khai triển:
a) (x + y)7;
b) (x – 2)7.Trả lời:
Tam giác Pascal ứng với n ≤ 7 là:

Vậy:
a)
b)
====== **** mời các bạn xem câu tiếp bên dưới **** =====