Phiếu bài tập tuần 27 – Toán 8

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

PHIẾU HỌC TẬP TOÁN 8 TUẦN 27

Hình học 8:         Các trường hợp đồng dạng của tam giác vuông

†††††††††

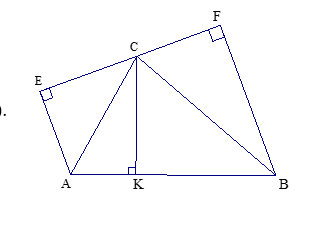
Bài 1:   Cho tam giác nhọn ABC có đường cao CK. Dựng ra phía ngoài tam giác ABC hai tam giác CAE và CBF tương ứng vuông góc tại E ; F và thỏa mãn $\widehat{ACE}=\widehat{CBA};\widehat{BCF}=\widehat{CAB}$ .

Chứng minh rằng: $C{K}^2=AE.BF$.

Bài 2:  Cho hình bình hành ABCD ( AC > BD) vẽ CE vuông góc với AB tại E, vẽ CF vuông góc với AD tại F. Chứng minh rằng $AB.AE+AD.AF=A{C}^2$.

Bài 3: Cho tam giác ABC vuông tại A. Lấy một điểm M bất kỳ trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E.

      a) Chứng minh: EA.EB = ED.EC.

      b) Chứng minh rằng khi điểm M di chuyển trên cạnh AC thì tổng BM.BD + CM.CA có giá trị không đổi.

      c) Kẻ DH vuông góc BC, (H $\in$ BC). Gọi P, Q lần lượt là trung điểm của các đoạn thẳng BH, DH. Chứng minh CQ vuông góc PD.

Bài 4: Cho tam giác ABC có hai góc B và C thỏa mãn điều kiện $\widehat{B}-\widehat{C}={90}^0$. Kẻ đường cao AH. Chứng minh rằng: $A{H}^2=BH.CH$ 

Bài 5 : Cho tam giác ABC cân tại A ($\widehat{A}<{90}^0$), đường cao AD, trực tâm H. Chứng minh hệ thức $C{D}^2=DH.DA$

 

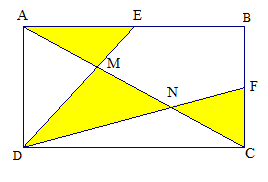
Bài 6: Cho hình chữ nhật ABCD có diện tích 150cm² (như hình vẽ). Gọi E, F là trung điểm AB và BC. Gọi M, N là giao điểm của DE, DF với AC. Tính tổng diện tích phần tô đậm.

 

– Hết – 

 

 

PHẦN HƯỚNG DẪN GIẢI

Bài 1:  

∆ACK và ∆CBF có :$\widehat{CKA}=\widehat{BFC}={90}^0;\widehat{CAK}=\widehat{BCF}\Rightarrow$

 ∆ACK ∆CBF (g.g)  (1).$\Rightarrow \frac{CK}{CA}=\frac{BF}{BC}$

Tương tự ta có ∆BCK  ∆CAE(g.g)  

$\Rightarrow \frac{CK}{CB}=\frac{AE}{AC}$(2)

Nhân từng vế của (1) và (2) ta được:

$\Rightarrow \frac{CK}{CA}\cdot \frac{CK}{CB}=\frac{BF}{BC}\cdot \frac{A\text{E}}{AC}\Rightarrow C{K}^2=A\text{E}.BF.$

Xem thêm