Lý thuyết Phân thức đại số (Chân trời sáng tạo 2023) hay, chi tiết | Lý thuyết Toán lớp 8

Lý thuyết Toán lớp 8 Bài 5: Phân thức đại số

A. Lý thuyết Phân thức đại số

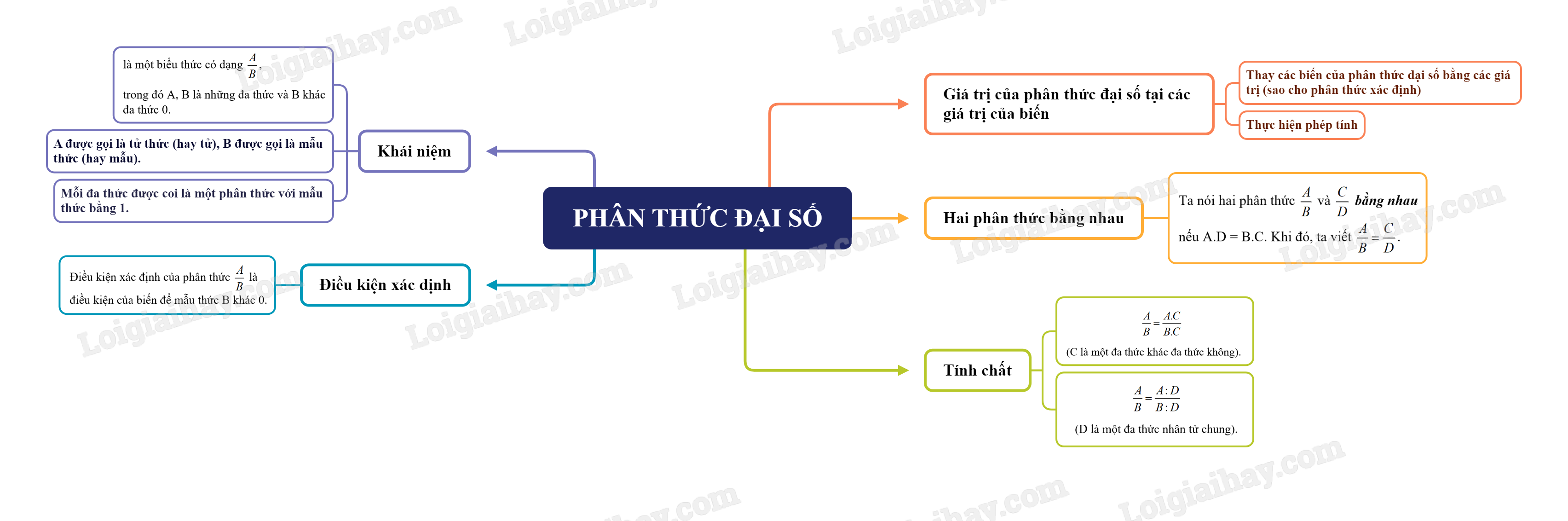
1. Khái niệm phân thức đại số

Một phân thức đại số (hay còn gọi là phân thức) là một biểu thức có dạng $\frac{A}{B}$, trong đó A, B là những đa thức và B khác đa thức 0.

A được gọi là tử thức (hay tử), B được gọi là mẫu thức (hay mẫu).

Chú ý: Mỗi đa thức được coi là một phân thức với mẫu thức bằng 1.

Ví dụ: $\frac{2x+1}{x-3};\frac{ab}{a+b};x^2+3x+2;\sqrt{2}$ là các phân thức đại số.

$\sqrt{x};\sqrt[3]{x}$ không phải là phân thức vì $\sqrt{x};\sqrt[3]{x}$ không phải là đa thức.

2. Điều kiện xác định của phân thức

Điều kiện xác định của phân thức $\frac{A}{B}$ là điều kiện của biến để mẫu thức B khác 0.

Khi thay các biến của phân thức đại số bằng các giá trị nào đó (sao cho phân thức xác định), rồi thực hiện các phép tính thì ta nhận được giá trị của phân thức đại số đó tại các giá trị của biến.

Ví dụ: Phân thức P = $\frac{x+3}{x-1}$ xác định khi $x-1\ne 0$ hay $x\ne 1$

Tại x = 3, $P=\frac{3+3}{3-1}=\frac{6}{2}=3$

3. Hai phân thức bằng nhau

Ta nói hai phân thức $\frac{A}{B}$ và $\frac{C}{D}$ bằng nhau nếu A.D = B.C. Khi đó, ta viết

$\frac{A}{B}=\frac{C}{D}$.

Ví dụ: Hai phân thức $\frac{x{y}^2}{xy+y}$ và $\frac{xy}{x+1}$ bằng nhau.

4. Tính chất

Khi nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

$\frac{A}{B}=\frac{A.C}{B.C}$ (C là một đa thức khác đa thức không).

Khi chia cả tử và mẫu của một phân thức cho cùng một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.

$\frac{A}{B}=\frac{A:D}{B:D}$ (D là một đa thức nhân tử chung).

Ví dụ: Để biến đổi phân thức $\frac{x-y}{y^2-x^2}$ thành $\frac{-1}{x+y}$, ta chia cả tử và mẫu của phân thức $\frac{x-y}{y^2-x^2}$ cho y – x, khi đó $\frac{x-y}{y^2-x^2}=\frac{-(y-x)}{(y-x)(y+x)}=\frac{-1}{x+y}$

 

B. Bài tập Phân thức đại số

Bài 1.Trong các biểu thức sau biểu thức nào là phân thức?

$\frac{\sqrt{x}-2}{2\text{x}+3};\frac{x+y}{x-y};3{\text{x}}^2-x+5.$

Hướng dẫn giải

Trong các biểu thức trên có $\frac{x+y}{x-y};3{\text{x}}^2-x+5$là phân thức.

Biểu thức $\frac{\sqrt{\text{x}}-2}{2\text{x}+3}$không phải là phân thức vì $\sqrt{\text{x}}$không phải là đa thức.

Bài 2.Viết điều kiện xác định của các phân thức sau:

a) x² + 3y – 1;

b) $\frac{2\text{x}+7}{5\text{x}-15}$

Hướng dẫn giải

a) Phân thức x² + 3y – 1 xác định với mọi giá trị của x.

b) Phân thức $\frac{2\text{x}+7}{5\text{x}-15}$xác định khi 5x – 15 ≠ 0 hay x ≠ 3.

Bài 3.Tìm giá trị của phân thức:

a) $\text{A}=\frac{2\text{x}-y}{4x^2-y^2}$ tại x = 5, y = 2;

b) $B=\frac{6{\text{x}}^2+12x+6}{x+1}$ tại x = 3.

Hướng dẫn giải

a) Điều kiện xác định của phân thức A là 4x² – y² ≠ 0 (nghĩa là các giá trị của x và y thỏa mãn 4x² – y² ≠ 0)

Ta có 

Khi x = 5, y = 2 thì 4x² – y² = 96 ≠ 0 thỏa mãn điều kiện xác định nên ta có:

$A=\frac{1}{2.5+2}=\frac{1}{12}.$

b) Điều kiện xác định của phân thức B là x + 1 ≠ 0 hay x ≠ – 1.

Ta có 

Khi x = 3 (thỏa mãn điều kiện xác định), ta có:

B = 6 . (3 + 1) = 6 . 4 = 24.

Bài 4.Hai phân thức $\frac{a^{3}b+a{b}^3}{ab(a-b)}$ và $\frac{a^2+b^2}{a-b}$ có bằng nhau không?

Hướng dẫn giải

Ta có:

•(a³b + ab³) . (a – b) = a³b(a – b) + ab³(a – b) = a⁴b – a³b² + a²b³ – ab⁴

•ab(a – b) . (a² + b²) = (a²b – ab²) . (a² + b²)

= a²b(a² + b²) – ab²(a² + b²)

= a⁴b + a²b³ – a³b² – ab⁴

Do đó (a³b + ab³) . (a – b) = ab(a – b) . (a² + b²)

Vậy $\frac{a^{3}b+a{b}^3}{ab(a-b)}=\frac{a^2+b^2}{a-b}.$

Bài 5.Rút gọn phân thức sau:

a) $\frac{6\text{a}{b}^3{c}^2}{12{\text{a}}^{2}bc}$.

b) $\frac{5{\text{x}}^5-5\text{x}}{x^2+1}$.

Hướng dẫn giải

Video bài giảng Toán 8 Phân thức đại số – Chân trời sáng tạo

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 4: Phân tích đa thức thành nhân tử

Lý thuyết Bài 5: Phân thức đại số

Lý thuyết Bài 6: Cộng, trừ phân thức

Lý thuyết Bài 7: Nhân, chia phân thức

Lý thuyết Bài 1: Hình chóp tam giác đều – Hình chóp tứ giác đều

Lý thuyết Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều