Lý thuyết Hình lăng trụ đứng (mới 2023 + bài tập) – Toán 8

Tài liệu Bài tập Hình lăng trụ đứng hình học toán 8 gồm các nội dung chính sau:

A. Lý thuyết

– tóm tắt lý thuyết ngắn gọn.

B. Các dạng bài tập

– gồm 2 bài tập vận dụng có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng Bài tập Hình lăng trụ đứng hình học toán 8.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

HÌNH LĂNG TRỤ ĐỨNG

A. Lý thuyết

1. HÌNH LĂNG TRỤ ĐỨNG

Định nghĩa: Hình lăng trụ đứng là hình có các mặt bên đều là những hình chữ nhật.

          Hình bên cho ta hình ảnh của hình lăng trụ đứng $ABCD.A_1{B}_1{C}_1{D}_1$, và ở đó:

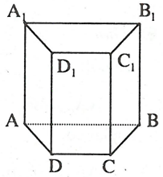1. Các điểm A, B, C, D, A₁, B₁, C₁, D₁ được gọi là các đỉnh.

2. Các đoạn $A{A}_1$, $B{B}_1$, $C{C}_1$, $D{D}_1$ song song với nhau và bằng nhau, chúng được gọi là các mặt bên.

3. Các mặt $AB{B}_{1}A$, $BC{C}_1{B}_1$, $CD{D}_1{C}_1$, $AD{D}_1{A}_1$ là những hình chữ nhật, chúng được gọi là các mặt bên.

4. Hai mặt $ABCD$, $A_1{B}_1{C}_1{D}_1$ là hai đáy.

5. Hình lăng trụ này có đáy là tứ giác nên gọi là lăng trụ tứ giác.

Ví dụ 1: Cho một hình lăng trụ đứng:

          – Hai mặt phẳng chứa hai đáy có song song với nhau hay không?

          – Các cạnh bên có vuông góc với hai mặt phẳng đáy hay không?

          – Các mặt bên có vuông góc với hai mặt phẳng đáy hay không?

Giải

Ta lần lượt có:

– Hai mặt phẳng chứa hai đáy có song song với nhau, bởi chúng đều chứa hai cặp đường thẳng cắt nhau và song song với nhau.

– Các cạnh bên có vuông góc với hai mặt phẳng đáy, bởi mỗi cạnh bên đều vuông góc với hai cạnh đáy cắt nhau.

– Các mặt bên có vuông góc với hai mặt phẳng đáy, bởi chúng chứa cạnh bên vuông góc với đáy.

Nhận xét: Như vậy:

• Hình hộp chữ nhật, hình lập phương cũng là những hình lăng trụ đứng.
• Hình lăng trụ đứng có đáy là hình bình hành được gọi là hình hộp đứng.

2. THÍ DỤ

Với hình vẽ trong phần 1, ta nhận thấy:

– Hai mặt đáy $ABCD$ và $A_1{B}_1{C}_1{D}_1$ là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song.

– Độ dài mỗi cạnh bên được gọi là chiều cao,  thí dụ chiều cao $A{A}_1$.

B. Các dạng bài tập

VÍ DỤ 1: $ABC.A_1{B}_1{C}_1$ là một lăng trụ đứng tam giác.

        a) Trong hình lăng trụ đó hãy chỉ ra những cặp mặt phẳng song song với nhau.

b) Trong hình lăng trụ đó hãy chỉ ra những cặp mặt phẳng vuông góc với nhau.

c) Sử dụng kí hiệu “//”, “$\perp$”, và “$\in$” điền vào các ô trong bảng sau:

	$A{A}_1$	$B{B}_1$	$C{C}_1$	AB	BC	AC	$A_1{B}_1$	$B_1{C}_1$	$A_1{C}_1$
$\left(ABC\right)$
$\left(A_1{B}_1{C}_1\right)$
$\left(AB{B}_1{A}_1\right)$

Xem thêm