Lý thuyết Hình bình hành (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8

Lý thuyết Toán lớp 8 Bài 12: Hình bình hành

A. Lý thuyết Hình bình hành

1. Khái niệm

Hình bình hành là tứ giác có các cạnh đối song song.

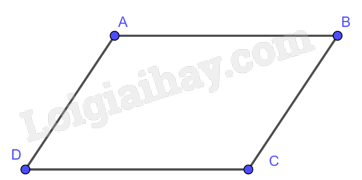
2. Tính chất

Trong hình bình hành:

– Các cạnh đối bằng nhau;

– Các góc đối bằng nhau;

– Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

3. Dấu hiệu nhận biết

– Tứ giác có các cạnh đối bằng nhau là một hình bình hành.

– Tứ giác có một cặp cạnh đối song song và bằng nhau là một hình bình hành.

– Tứ giác có các góc đối bằng nhau là một hình bình hành.

– Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là một hình bình hành.

Ví dụ: 

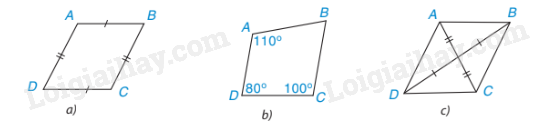
Hình a và c là hình bình hành do:

Hình a có các cặp cạnh đối bằng nhau.

Hình b có các đường chéo cắt nhau tại trung điểm của mỗi đường.

B. Bài tập Hình bình hành

Bài 1. Tính các góc còn lại của hình bình hành ABCD trong hình dưới đây.

Hướng dẫn giải

Vì tứ giác ABCD là hình bình hành nên $\hat{B}=\hat{D}=60°$

Theo định lí tổng các góc trong một tứ giác ta có:

 $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$ suy ra $\hat{A}+\hat{C}=240°\Rightarrow \hat{A}=\hat{C}=120°$ .

Bài 2. Trong mỗi trường hợp sau, tứ giác nào là hình bình hành, tứ giác nào không phải là hình bình hành? Vì sao?

Hướng dẫn giải

+ Tứ giác EFGH có $\hat{F}=360°-(\hat{E}+\hat{H}+\hat{G})=60°$

Suy ra $\hat{F}=\hat{H}$  mà $\hat{G}=\hat{E}$  nên theo dấu hiệu nhận biết của hình bình hành ta có tứ giác EFGH là hình bình hành.

+ Tứ giác MNPQ không là hình bình hành vì ta dễ dàng tính được $\hat{M}=100°\ne \hat{P}$

+ Tứ giác ABCD là hình bình hành vì có các cạnh đối bằng nhau: AB = CD và AD = BC.

Bài 3. Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh Từ đó suy ra tứ giác MBND là hình bình hành.

Hướng dẫn giải

+ Vì O là giao điểm của hai đường chéo của hình bình hành ABCD nên O là trung điểm của BD và AC.

Lại có: AB // CD nên $\widehat{OCN}=\widehat{OAM}$  (hai góc so le trong)

+ Xét $\Delta OAM$ và $\Delta OCN$  có:

$\widehat{OCN}=\widehat{OAM}$(chứng minh trên)

OA = OC (O là trung điểm AC)

$\widehat{AOM}=\widehat{CON}$(hai góc đối đỉnh)

Do đó $\Delta OAM=\Delta OCN$  (góc – cạnh – góc)

Suy ra OM = ON hay O là trung điểm MN.

+ Xét tứ giác MBND có hai đường chéo MN và BD cắt nhau tại trung điểm O của mỗi đường, suy ra tứ giác MBND là hình bình hành (dấu hiệu nhận biết).

Video bài giảng Toán 8 Bài 12: Hình bình hành – Kết nối tri thức

Xem thêm các bài tóm tắt lý thuyết Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 11: Hình thang cân

Lý thuyết Bài 12: Hình bình hành

Lý thuyết Bài 13: Hình chữ nhật

Lý thuyết Bài 14: Hình thoi và hình vuông

Lý thuyết Bài 15: Định lí Thalès trong tam giác

Lý thuyết Bài 16: Đường trung bình của tam giác

Xem thêm các bài tóm tắt lý thuyết chương Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Chương 1: Đa thức

Lý thuyết Chương 2: Hằng đẳng thức đáng nhớ và ứng dụng

Lý thuyết Chương 3: Tứ giác

Lý thuyết Chương 4: Định lí Thalès

Lý thuyết Chương 5: Dữ liệu và biểu đồ