Tài liệu Bài tập Đối xứng trục hình học toán 8 gồm các nội dung chính sau:
A. Lý thuyết
– tóm tắt lý thuyết ngắn gọn.
B. Các dạng bài tập
– gồm 9 bài tập vận dụng giúp học sinh tự rèn luyện cách giải các dạng Bài tập Đối xứng trục hình học toán 8.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

ĐỐI XỨNG TRỤC
A. Lý thuyết
|
Hai điểm A, B gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó. Quy ước: Nếu điểm M nằm trên đường thẳng d thì điểm đối xứng với M qua đường thẳng d cũng là điểm M. Hai hình gọi là đối xứng với nhau qua đường thẳng d nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng d và ngược lại. Đường thẳng d gọi là trục đối xứng của hai hình đó. Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau. Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H. Ta nói hình H có trục đối xứng Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân |
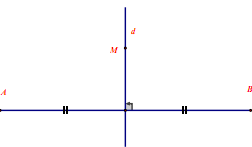
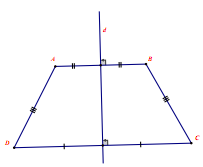
B. Các dạng bài tập:
Bài 1. Cho góc xOy = 50° và điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, điểm C đối xứng với A qua Oy.
a) So sánh các độ dài OB và OC.
b) Tính số đo góc BOC .
ĐS: b) BOC = 100°.
Bài 2. Cho tam giác nhọn ABC, trực tâm H. Gọi K là điểm đối xứng với H qua BC.
a) Chứng minh hai tam giác BHC và BKC bằng nhau.
b) Cho BAC = 70° . Tính số đo góc BKC.
ĐS: b) BKC = 110°.
Bài 3. Cho hình thang vuông ABCD ( A = D = 90°). Gọi K là điểm đối xứng với B qua AD, E là giao điểm của CK và AD. Chứng minh CED = AEB.
Bài 4. Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K lần lượt là điểm đối xứng với điểm H qua các cạnh AB, AC. Chứng minh:
a) Ba điểm I, A, K thẳng hàng.
b) Tứ giác BIKC là hình thang.
c) IK = 2AH .
Bài 5. Cho tam giác ABC, các phân giác BM và CN cắt nhau tại I. Từ A vẽ các đường vuông góc với BM và CN, chúng cắt BC thứ tự ở E và F. Gọi I’ là hình chiếu của I trên BC. Chứng minh rằng E và F đối xứng nhau qua II’.
Bài 6. Cho hai điểm A, B nằm trong một nửa mặt phẳng bờ là đường thẳng d. Tìm điểm sao cho MA + MB ngắn nhất.
Bài 7. Cho góc xOy = 60° và điểm A nằm trong góc đó. Gọi B, C lần lượt là hai điểm đối xứng với điểm A qua Ox, Oy.
a) Chứng minh tam giác BOC là tam giác cân. Tính các góc của tam giác đó.
b) Tìm điểm và điểm sao cho tam giác AIK có chu vi nhỏ nhất.
ĐS: a) BOC = 120°, OBC = OCB = 30°
b) I, K là giao điểm của đường thẳng BC với các tia Ox và Oy.
Bài 8. Cho tam giác ABC, Cx là phân giác ngoài của góc C. Trên Cx lấy điểm M (khác C). Chứng minh rằng: MA + MB > CA + CB.
Bài 9. Cho góc nhọn xOy và điểm A ở trong góc đó . Tìm điểm B ở trên tia Ox và điểm C ở trên tia Oy sao cho chu vi tam giác ABC là nhỏ nhất.