Giải bài tập Toán lớp 8 Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 20 sgk Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử
a) ;
b) .
Phương pháp giải: Áp dụng hằng đẳng thức số
Lời giải:
a)
b)
Trả lời câu hỏi 2 trang 20 sgk Toán 8 Tập 1: Tính nhanh:
Phương pháp giải: Áp dụng hằng đẳng thức số .
Lời giải:
Câu hỏi và bài tập (trang 20, 21 sgk Toán 8 Tập 1)
Bài 43 trang 20 sgk Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:
a) ;
b);
c) ;
d)
Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ:
Lời giải:
a)
b)
c)
d)
Bài 44 trang 20 sgk Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:
a) ;
b) ;
c) ;
d) ;
e)
Lời giải:
a)
Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ: Tổng hai lập phương.
Lời giải:
b)
Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ: Hiệu hai lập phương, bình phương một tổng, bình phương một hiệu, hiệu hai bình phương.
Lời giải:
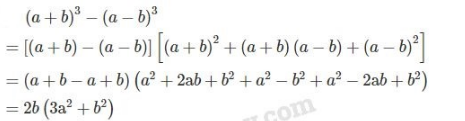
c)
Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ: Tổng hai lập phương, bình phương một tổng, bình phương một hiệu, hiệu hai bình phương.
Lời giải:
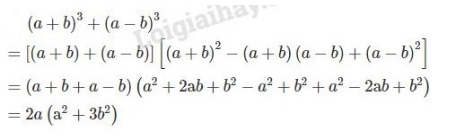
d)
Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ: Lập phương một tổng.
Lời giải:
e)
Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ: Lập phương một hiệu.
Lời giải:
Bài 45 trang 20 sgk Toán 8 Tập 1: Tìm , biết:
a) ;
b)
Lời giải:
a)
Phương pháp giải: – Phân tích các biểu thức ở vế trái thành nhân tử, sau đó áp dụng tính chất:
hoặc
– Áp dụng hằng đẳng thức hiệu hai bình phương.
Lời giải:
hoặc
+) Với
+) Với
Vậy hoặc
Cách khác:
hoặc
hoặc
b)
Phương pháp giải: – Phân tích các biểu thức ở vế trái thành nhân tử, sau đó áp dụng tính chất:
hoặc
– Áp dụng hằng đẳng thức bình phương một hiệu.
Lời giải:
Vậy
Bài 46 trang 21 sgk Toán 8 Tập 1: Tính nhanh:
a) ;
b) ;
c) .
Phương pháp giải: Áp dụng hằng đẳng thức hiệu hai bình phương để phân tích các đa thức đó thành nhân tử.
Lời giải:
a)
b)
c)
.
Lý thuyết Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
1. Các kiến thức cần nhớ: Ta sử dụng các hằng đẳng thức đáng nhớ đã học để thực hiện phép phân tích đa thức thành nhân tử.
Các hằng đẳng thức đáng nhớ:
.
.
.
.
.
.
.
Ví dụ:
Chú ý: Khi áp dụng phương pháp dùng hằng đẳng thức để phân tích đa thức thành nhân tử, ta cần lưu ý:
– Trước tiên nhận xét xem các hạng tử của đa thức có chứa nhân tử chung không ? Nếu có thì áp dụng phương pháp đặt thành nhân tử chung.
– Nếu không thì xét xem có thể áp dụng hằng đẳng thức đáng nhớ để phân tích thành nhân tử hay không ?
Chú ý: Đôi khi phải dùng quy tắc dấu ngoặc sau đó mới áp dụng được hằng đẳng thức.
Ví dụ:
2. Các dạng toán thường gặp:
Dạng 1: Phân tích đa thức thành nhân tử
Phương pháp: Ta sử dụng các hằng đẳng thức đã học để phân tích đa thức đã cho thành nhân tử.
Dạng 2: Tìm
Phương pháp: Ta sử dụng các hằng đẳng thức đã học để phân tích đa thức đã cho thành nhân tử.
Từ đó đưa về dạng tìm thường gặp như
Dạng 3: Tính giá trị biểu thức thỏa mãn điều kiện cho trước
Phương pháp: Ta biến đổi biểu thức đã cho để có thể sử dụng được điều kiện ở giả thiết. Từ đó tính giá trị biểu thức.