Giải SGK Toán 8 Ôn tập chương 4 Hình học

Giải bài tập Toán lớp 8 Ôn tập chương 4 Hình học

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 125 Toán 8 Tập 2: Hãy quan sát phần trong của lớp học rồi chỉ ra:

a) Các đường thẳng song song với nhau

b) Các đường thẳng cắt nhau

c) Các mặt phẳng song song với nhau

d) Các đường thẳng vuông góc với nhau

e) Các đường thẳng vuông góc với các mặt phẳng

f) Các mặt phẳng vuông góc với nhau

Trả lời:

Học sinh quan sát trên thực tế

Câu hỏi 2 trang 126 Toán 8 Tập 2: a) Hình lập phương có mấy mặt, mấy cạnh, mấy đỉnh? Các mặt là những hình gì?

b) Hình hộp chữ nhật có mấy mặt, mấy cạnh, mấy đỉnh ?

c) Hình lăng trụ đứng tam giác có mấy cạnh, mấy đỉnh , mấy mặt?

Trả lời:

a) Hình lập phương có 6 mặt, 12 cạnh, 8 đỉnh. Các mặt là những hình vuông.

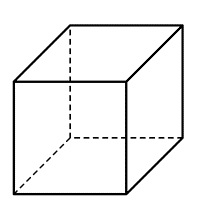
b) Hình hộp chữ nhật có 6 mặt, 12 cạnh, 8 đỉnh.

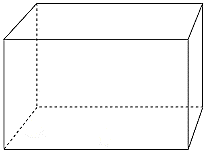
c) Hình lăng trụ đứng tam giác có 9 cạnh, 6 đỉnh , 5 mặt.

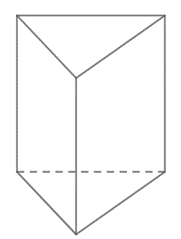
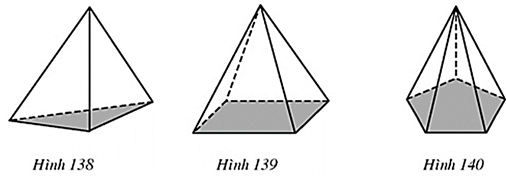
Câu hỏi 3 trang 126 Toán 8 Tập 2: Hãy gọi tên các hình chóp theo những hình vẽ dưới đây:

Trả lời:

Hình 138: Hình chóp tam giác

Hình 139: Hình chóp tứ giác

Hình 140: Hình chóp ngũ giác

Bài tập (trang 127; 128; 129)

Bài 51 trang 127 Toán 8 Tập 2: Tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao h và đáy lần lượt là:

a) Hình vuông cạnh a;

b) Tam giác đều cạnh a;

c) Lục giác đều cạnh a;

d) Hình thang cân, đáy lớn là 2a, các cạnh còn lại bằng a;

e) Hình thoi có hai đường chéo là 6a và 8a.

Lời giải:

Gọi h là chiều cao của hình lăng trụ đứng.

a)

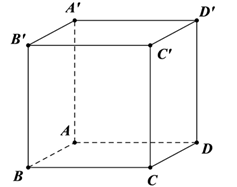
Diện tích xung quanh: S_xq  = 2.p.h = 4.a.h

Diện tích 1 đáy là: S_d = a².

Diện tích toàn phần của hình lăng trụ:

S_tp = S_xq  + 2.S_d = 4ah + 2a².

Thể tích lăng trụ: V = S_d.h  = a².h

b)

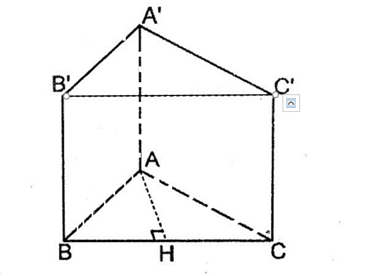
Gọi hình lăng trụ đứng đáy là tam giác đều là ABC. A’B’C’.

Gọi H là trung điểm BC.

Vì đáy ABC là tam giác đều nên đường trung tuyến đồng thời là đường cao.

Chiều cao của tam giác đều :

$AH=\sqrt{A{B}^2-B{H}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}$

Diện tích xung quanh:

S_xq = 2.p.h = 3ah

Diện tích một đáy:

 $S_d=\frac{1}{2}.a.\frac{a\sqrt{3}}{2}=\frac{a^2\sqrt{3}}{4}$

Diện tích toàn phần:

$S_{tp}=3ah\text{}+\text{\hspace{0.17em}\hspace{0.17em}}2.\frac{a^2\sqrt{3}}{4}=3ah\text{}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{a^2\sqrt{3}}{2}$

Thể tích:

$V=S_d.h=\frac{a^2\sqrt{3}}{4}.h=\frac{a^{2}h\sqrt{3}}{4}$

c)

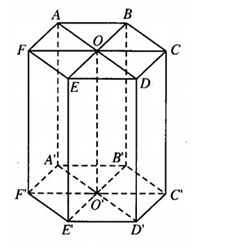
Gọi hình lăng trụ đứng có đáy là lục giác đều là ABCDEF. A’B’C’D’E’F’.

Gọi O và O’ lần lượt là tâm 2 đáy.

Diện tích xung quanh:

S_xq = 2p.h = 6ah.

Vì đáy ABCDEF là lục giác đều nên lục giác này được chia ra thành 6 tam giác đều cạnh bằng a.

Diện tích tam giác đều cạnh a (theo câu b) là:

 $\frac{a^2\sqrt{3}}{4}$

Do đó, diện tích 1 đáy của hình lăng trụ là

 $S_d=6.\frac{a^2\sqrt{3}}{4}=\frac{3a^2\sqrt{3}}{2}$

Diện tích toàn phần:

$S_{tp}=S_{xq}+\text{\hspace{0.17em}\hspace{0.17em}}2S_d=6ah+\text{}2.\frac{3a^2\sqrt{3}}{2}=6ah+\text{\hspace{0.17em}}3a^2\sqrt{3}$

Thể tích lăng trụ:

$V=S_d.h=\frac{3a^2\sqrt{3}}{2}.h=\frac{3a^{2}h\sqrt{3}}{2}$

d)

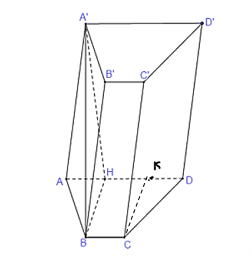
Gọi hình lăng trụ là ABCD.A’B’C’D’ có đáy ABCD là hình thang cân: AB = BC = CD = a; AD = 2a

Diện tích  xung quanh:

  S_xq = 2ph = (2a + a + a+ a) .h = 5ah

Trong mp(ABCD) kẻ; BH vuông AD và CK vuông AD.

Ta có, tứ giác BCKH là hình bình hành (vì có các cạnh đối đôi một song song )

Suy ra: HK = BC = a.

Suy ra: $AH=HK=\frac{AD-HK}{2}=\frac{a}{2}$

Tam giác AHB vuông tại B nên:

$BH=\sqrt{A{B}^2-A{H}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}$

Diện tích 1 đáy của hình lăng trụ là:

$S_d=\frac{(2a+\text{\hspace{0.17em}\hspace{0.17em}}a).\frac{a\sqrt{3}}{2}}{2}=\frac{3a^2\sqrt{3}}{4}$

Diện tích toàn phần:

$S_{tp}=5ah+\text{\hspace{0.17em}\hspace{0.17em}}2.\frac{3a^2\sqrt{3}}{4}=5ah+\text{\hspace{0.17em}\hspace{0.17em}}\frac{3a^2\sqrt{3}}{2}$

Thể tích của lăng trụ:

$V=S.h=\frac{3a^2\sqrt{3}}{4}.h=\frac{3a^{2}h\sqrt{3}}{4}$

e)

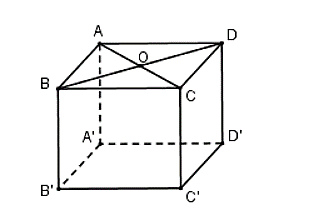
Gọi O là giao điểm của AC và BD.

Suy ra: O là trung điểm của AC và trung điểm của BD.

Cạnh của hình thoi là:

$BC=\sqrt{O{B}^2+\text{\hspace{0.17em}\hspace{0.17em}}O{C}^2}=\sqrt{{\left(3a\right)}^2+\text{\hspace{0.17em}\hspace{0.17em}}{\left(4a\right)}^2}=5a$

Diện tích xung quanh của hình lăng trụ là:

S_xq = 2ph = 4.5.a.h = 20ah

Diện tích một đáy của lăng trụ là:

$S_d=\frac{1}{2}.6a.8a=24a^2$

Diện tích toàn phần:

$S_{tp}=20ah+2.24a^2=20ah+\text{\hspace{0.17em}\hspace{0.17em}}48a^2$

Thể tích lăng trụ: V = S. h = 24a².h

Bài 52 trang 128 Toán 8 Tập 2: Tính diện tích toàn phần của thanh gỗ như ở hình 142 (mặt trước, mặt sau của thanh gỗ là những hình thang cân, bốn mặt còn lại đều là những hình chữ nhật, cho biết $\sqrt{10}$ ≈ 3,16).

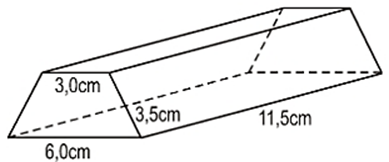
Hình 142

Lời giải:

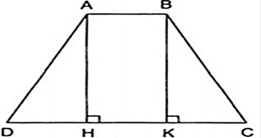
Thanh gỗ dạng hình lăng trụ đứng, đáy là hình thang cân. Ta tìm chiều cao của hình thang cân.

Trong mặt phẳng đáy, kẻ AH vuông góc CD, BK vuông góc với CD.

Xét tam giác AHD và tam giác BKC có:

AD = BC (tính chất hình thang cân)

$\widehat{AHB}=\widehat{BKC}=90°$

$\stackrel{⏜}{ADH}=\widehat{BCK}$ (tính chất hình thang cân)

Do đó: $\Delta AHD=\Delta BKC$ (cạnh huyền – góc nhọn)

$\Rightarrow DH=CK$(hai cạnh tương ứng)

Ta lại có:

AB // HK (do ABCD là hình thang)

AH // BK (quan hệ từ vuông góc đến song song)

Do đó AHKB là hình bình hành nên AB = HK (tính chất hình bình hành)

Ta có:

DH + CK = DC – HK

$\iff$2DH = DC – AB

$\Rightarrow$$DH=\frac{1}{2}\text{}(\text{}DC-AB\text{})$

$=\frac{1}{2}(\text{}6-3)=1,5cm$

Chiều cao hình thang là:

$AH=\sqrt{A{D}^2-D{H}^2}=\sqrt{3,5^2-1,5^2}=\sqrt{10}\approx 3,16cm$

Diện tích xung quanh của hình lăng trụ là:

S_xq = 2ph = ( 3 + 6 + 3,5 + 3,5).11,5 = 184 cm².

Diện tích một đáy là:

$S_d=\frac{(3+6).3,16}{2}=14,22c{m}^2$

Diện tích toàn phần:

 S_tp  = S_xq + 2S_d = 184 + 2. 14,22 = 212,44 cm²

Bài 53 trang 128 Toán 8 Tập 2: Thùng chứa của xe ở hình 143 có dạng lăng trụ đứng tam giác, các kích thước cho trên hình. Hỏi dung tích của thùng chứa là bao nhiêu?

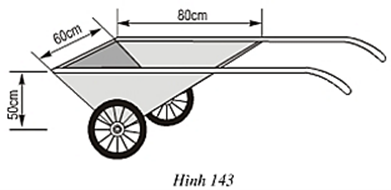
Lời giải:

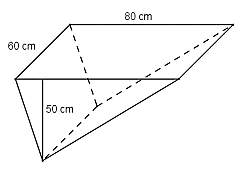
Thùng chứa là một hình lăng trụ đứng đáy là tam giác

Diện tích đáy là:

 $S_d=\frac{1}{2}ah=\frac{1}{2}.80.50=2000c{m}^2$

Thể tích là: V = S. h = 2000. 60 = 120 000 cm³

Bài 54 trang 128 Toán 8 Tập 2: Người ta muốn đổ một tấm bê tông dày 3cm, bề mặt của tấm bê tông có các kích thước như ở hình 144.

a) Số bê tông cần phải có là bao nhiêu?

b) Cần phải có bao nhiêu chuyến xe để chở số bê tông cần thiết đến chỗ đổ bê tông, nếu mỗi xe chứa được 0,06m³? (Không tính số bê tông dư thừa hoặc rơi vãi)

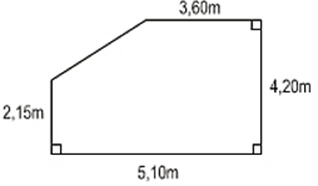
Hình 144

Lời giải:

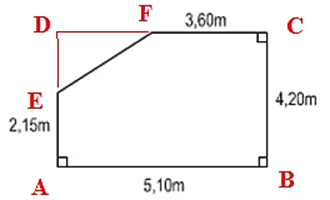
Từ hình đã cho, ta vẽ thêm hình để được một hình chữ nhật ABCD.

Ta có: DE = DA – EA = 4,2 – 2,15 = 2,05 m

DF = DC – FC = 5,1 – 3,6 = 1,5 m

Diện tích hình chữ nhật ABCD là:

S_ABCD = 5,1 . 4,2 = 21,42 m²

Diện tích tam giác vuông DEF là:

$S_{D\text{}E\text{}F}=\frac{1}{2}.D\text{}E\text{}.DF=\frac{1}{2}.2,05.1,5=1,5375\approx 1,54m^2$

Suy ra: S_ABCFE = S_ABCD – S_DEF = 19,88m².

a) Số bê tông cần đổ chính là thể tích của lăng trụ có đáy là ABCFE, chiều cao 3cm = 0,03 m.

V = S.h = 19,88. 0,03 = 0, 5964  m^3.

b) Nếu mỗi chuyến xe chở được 0,06m³ bê tông thì số chuyến xe là:

$0,5964:0,06=9,94\approx 10$  chuyến.

Bài 55 trang 128 Toán 8 Tập 2: A, B, C, D là các đỉnh của một hình hộp chữ nhật. Hãy quan sát hình 145 rồi điền số thích hợp vào các ô trống ở bảng sau:

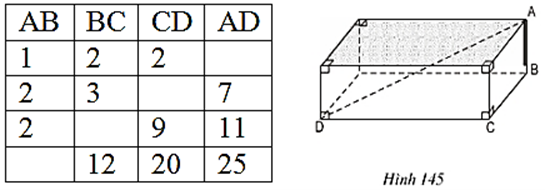
Lời giải:

Ta có;

+) Dòng 2:

$AD=\sqrt{A{B}^2+B{C}^2+\text{\hspace{0.17em}}C{D}^2}=\sqrt{1^2+\text{}{2}^2+\text{}{2}^2}=3$

+) Dòng 3:

$BD=\sqrt{A{D}^2-A{B}^2}=\sqrt{7^2-2^2}=\sqrt{45}CD=\sqrt{B{D}^2-B{C}^2}=\sqrt{45-3^2}=6$

+) Dòng 4:

$BD=\sqrt{A{D}^2-A{B}^2}=\sqrt{{11}^2-2^2}=\sqrt{117}BC=\sqrt{B{D}^2-D{C}^2}=\sqrt{117-9{}^2}=6$

+) Dòng 5.

$BD\text{\hspace{0.17em}\hspace{0.17em}}=\sqrt{C{D}^2+B{C}^2}=\sqrt{{20}^2+\text{\hspace{0.17em}}{12}^2}=\sqrt{544}AB=\sqrt{A{D}^2-B{D}^2}=\sqrt{{25}^2-544}=9$

Ta có bảng sau:

AB	BC	CD	AD
1	2	2	3
2	3	6	7
2	6	9	11
9	12	20	25

Bài 56 trang 129 Toán 8 Tập 2: Một cái lều ở trại hè có dạng lăng trụ đứng tam giác (với các kích thước trên hình 146):

a) Tính thể tích khoảng không ở bên trong lều.

b) Số vải bạt cần phải có để dựng lều đó là bao nhiêu?

(Không tính các mép và nếp gấp của lều).

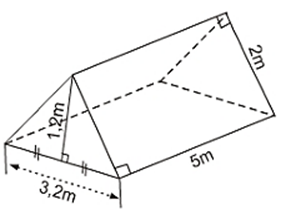
Hình 146

Lời giải:

a) Cái lều là lăng trụ đứng có đáy là tam giác

Diện tích đáy là:

 $S=\frac{1}{2}.3,2.1,2=1,92m^2$

Thể tích khoảng không ở bên trong lều là:

V = S.h = 1,92. 5= 9,6 m³.

b) Số vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là 5m và 3,2m.

Diện tích xung quanh lăng trụ là:

S_xq = 2ph = (2 + 2 + 3,2). 5 = 36 m²

Diện tích toàn phần là:  36 + 2. 1,92 = 39,84 m²

Diện tích mặt bên kích thước 5m và 3,2m là:

S = 5. 3,2 = 16m²

Vậy số bạt cần có để dựng lều là: 39,84 – 16 = 23,84m²

Bài 57 trang 129 Toán 8 Tập 2: Tính thể tích của hình chóp đều, hình chóp cụt đều sau đây (h.147 và h.148) ( $\sqrt{3}$ ≈ 1,73)

Hướng dẫn: Hình chóp L.EFGH cũng là hình chóp đều.

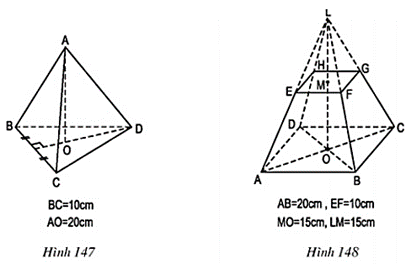
Lời giải:

+ Hình 147:

Gọi H là trung điểm của BC. Do ABCD là hình chóp tam giác đều nên BDC là tam giác đều do đó DH vừa là đường trung tuyến vừa là đường cao của tam giác BCD.

Chiều cao của tam giác đều BCD cạnh 10 cm là:

$DH=\sqrt{B{D}^2-B{H}^2}=\sqrt{{10}^2-5^2}=\frac{10\sqrt{3}}{2}\approx 8,65cm$

Diện tích đáy của hình chóp là:

$S=\frac{1}{2}BC.DH\text{}=\frac{1}{2}\mathrm{.10.}8,65=43,25c{m}^2$

Thể tích hình chóp đều là:

$V=\frac{1}{3}.S.h=\frac{1}{3}.43,25.20=288,33c{m}^3$

+ Hình 148 :

Thể tích của hình chóp cụt đều chính là hiệu của thể tích hình chóp đều L.ABCD với thể tích của hình chóp đều L.EFGH

Ta có: LO= LM + MO = 15 + 15 = 30 cm

+ Tính thể tích của hình chóp đều L.ABCD

Diện tích đáy: S = AB²  = 20² = 400 cm²

Thể tích

 $V=\frac{1}{3}S.h=\frac{1}{3}\mathrm{.400.}30=4000c{m}^3$

+ Tính thể tích hình chóp đều L.EFGH

Diện tích đáy EFGH là: S = EF² = 10² = 100 cm²

Thể tích:

 $V=\frac{1}{3}Sh=\frac{1}{3}\mathrm{.100.15}=500c{m}^3$

Do đó, thể tích hình chóp cụt đều là:

V = 4000 – 500 = 3500 cm³

Bài 58 trang 129 Toán 8 Tập 2: Tính thể tích của hình cho trên hình 149 với các kích thước kèm theo.

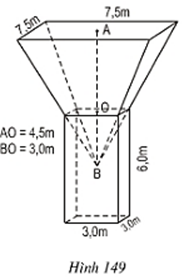
Lời giải:

Thể tích cần tính bao gồm một hình hộp chữ nhật và một hình chóp cụt:

V_hôp = 3.3.6 = 54 m³

Thể tích hình chóp với đường cao BA là:

BA = BO + OA = 3 + 4,5 = 7,5 cm

$V_1=\frac{1}{3}.S_1.h_1=\frac{1}{3}.7,5^2.7,5=140,625m^3$

Thể tích hình chóp với đường cao BO = 3m là:

$V_2=\frac{1}{3}{S}_2{h}_2=\frac{1}{3}.3^3.3=9m^3$

Thể tích hình chóp cụt là:

V = V₁  – V₂ = 140,625 – 9 = 131, 625 m³.

Thể tích cần tính là :

V = V_hôp + V = 54 + 131, 625 = 185,625 m³