Giải SGK Toán 8 Bài 6: Thể tích của hình lăng trụ đứng

Giải bài tập Toán lớp 8 Bài 6: Thể tích của hình lăng trụ đứng

Trả lời câu hỏi giữa bài

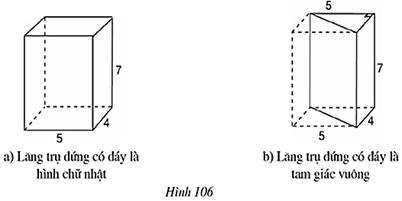
Câu hỏi 1 trang 112 Toán 8 Tập 2: Quan sát các lăng trụ đứng ở hình 106

– So sánh thể tích của lăng trụ đứng tam giác và thể tích hình hộp chữ nhật.

– Thể tích lăng trụ đứng tam giác có bằng diện tích đáy nhân với chiều cao hay không? Vì sao?

Lời giải:

– Thể tích lăng trụ đứng tam giác bằng một nửa thể tích hình hộp chữ nhật

– Thể tích lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao

Vì thể tích hình hộp chữ nhật là: 5.4.7 = 140

⇒ Thể tích lăng trụ đứng tam giác là 140 : 2 = 70

Diện tích đáy lăng trụ đứng tam giác là: $\frac{1}{2}$ . 5 .4 = 10

Chiều cao lăng trụ đứng tam giác là 7

Mà 70 = 10 .7

Bài tập (trang 113; 114; 115; 116)

Bài 27 trang 113 Toán 8 Tập 2: Quan sát hình 108 rồi điền số thích hợp vào các ô trống ở bảng sau:

B	5	6	4
H	2			4
h1	8	5		10
Diện tích 1 đáy		12	6
Thể tích			12	50

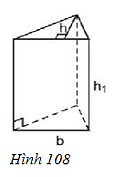
Lời giải:

Ta có: Diện tích đáy:

 $S=\frac{1}{2}b.h$

Thể tích V = S.h₁

+ Cột 2:

$S=\frac{1}{2}b.h=\frac{1}{2}\mathrm{.5.2}=5V\text{}=S.h_1=5.8=40$

+ Cột 3:

$S=\frac{1}{2}b.h\Rightarrow h=\frac{2S}{b}=\frac{2.12}{6}=4V=S.h_1=12.5=60$

+ Cột 4.

$h=\frac{2S}{b}=\frac{2.6}{4}=3V=S.h_1\Rightarrow h_1=\frac{V}{S}=\frac{12}{6}=2$

+ Cột 5:

$V=S.h_1=\frac{1}{2}b.h.h_1\Rightarrow b=\frac{2V}{h.h_1}=\frac{2.50}{4.10}=2,5S=\frac{1}{2}bh=\frac{1}{2}.2,5.4=5$

Ta có bảng sau:

b	5	6	4	2,5
h	2	4	3	4
h1	8	5	2	10
Diện tích 1 đáy	5	12	6	5
Thể tích	40	60	12	50

Bài 28 trang 114 Toán 8 Tập 2: Thùng đựng của một máy cắt cỏ có dạng lăng trụ đứng tam giác (h.109). Hãy tính dung tích của thùng.

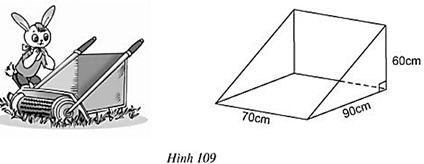
Lời giải:

Lăng trụ đứng tam giác có đáy là tam giác vuông, nên diện tích đáy là:

$S=\frac{1}{2}.60.90=2700\left(c{m}^2\right)$

Thể tích lăng trụ V = Sh = 2700.70 = 189000 (cm³)

Vậy dung tích của thùng là 189000cm³

Bài 29 trang 114 Toán 8 Tập 2: Các kích thước của một bể bới được cho trên hình 110 (mặt nước có dạng hình chữ nhật). Hãy tính xem bể chứa được bao nhiêu mét khối nước khi nó đầy ắp nước?

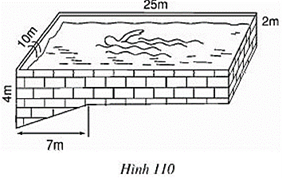
Lời giải:

Bể bơi được chia thành hai phần: phần hình hộp chữ nhật với các kích thước là 10m, 25m, 2m; phần hình lăng trụ đứng với đáy là tam giác vuông có hai cạnh góc vuông là 2m, 7m, chiều cao 10m.

Thể tích hình hộp chữ nhật là:

V = 10.25.2= 500 (m³)

Thể tích lăng trụ đứng tam giác:       

$V=S.h=\frac{1}{2}\mathrm{.2.7.10}=70m^3$

Vậy thể tích bể bơi khi đầy ắp nước là:

500 + 70 = 570m³

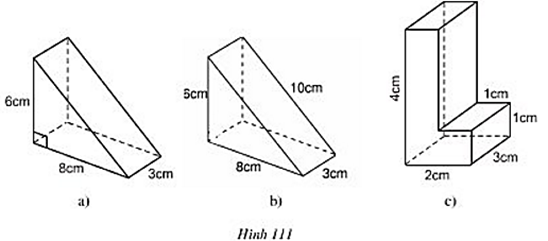
Bài 30 trang 114 Toán 8 Tập 2: Các hình a, b, c (h.111) gồm một hoặc nhiều lăng trụ đứng. Hãy tính thể tích và diện tích toàn phần của chúng theo các kích thước đã cho trên hình.

Lời giải:

Hình a: là lăng trụ đứng, đáy là tam giác vuông có 2 cạnh góc vuông là 6 cm và 8cm.

Suy ra, độ dài cạnh huyền là:

$\sqrt{6^2\text{}+\text{\hspace{0.17em}}{8}^2}=10cm$, chiều cao lăng trụ là 3cm

Diện tích đáy là: 

 $S=\frac{1}{2}.6.8=24c{m}^2$

Thể tích: V = S.h = 24.3 = 72cm³.

Diện tích xung quang lăng trụ:

S_xq = 2p.h = ( 6 + 8 + 10). 3 = 72cm²

Diện tích toàn phần:

S_tp = S_xq + 2S_đáy = 72 + 2.24 = 120 cm²

+ Hình b là hình lăng trụ đứng có đáy là tam giác với độ dài 3 cạnh là 6cm; 8cm; 10cm. Chiều cao lăng trụ là 3cm.

Ta có: 6² + 8² = 100 = 10²

Suy ra, đáy của lăng trụ là tam giác vuông với 2 cạnh góc vuông là 6cm và 8cm.

Diện tích đáy:

 $S=\frac{1}{2}6.8=24c{m}^2$

Thể tích: V = S.h = 24.3 = 72cm³

Diện tích xung quanh của lăng trụ là:

S_xq = 2.p.h = ( 6 + 8+ 10) . 3 = 72 cm²

Diện tích toàn phần:

S_tp = S_xq + 2S_đáy = 72 + 2.24 = 120 cm²       

+ Hình c: là hình gồm 2 lăng trụ đứng:

Hình lăng trụ 1 là hình hộp chữ nhật có các kích thước: 4 cm; 1 cm; 3 cm

Hình lăng trụ 2 là hình hộp chữ nhật có các kích thước 1cm; 1cm; 3cm

Thể tích lăng trụ 1: V₁ = 4.1.3 = 12 (cm³)

Thể tích lăng trụ hai là: V₂ = 1.1.3 = 3 cm³

Thể tích lăng trụ đã cho là 12 + 3 = 15 cm³

Diện tích xung quanh của lăng trụ 1:

S_xq1 = 2.(3 + 1).4 = 32m²

Diện tích 1 đáy của lăng trụ 1: S_d1 = 3.1 = 3cm²

Diện tích toàn phần của lăng trụ 1: 32 + 2. 3 = 38cm²

Diện tích xung quanh của lăng trụ 2:

S_xq2 = 2.(1+ 3).1 = 8cm²

Diện tích 1 đáy của lăng trụ 2: S_d2 = 3.1 = 3cm²

Diện tích toàn phần của lăng trụ 2: 8 + 2. 3 = 14cm²

Diện tích toàn phần của lăng trụ đã cho bằng tổng diện tích toàn phần của lăng trụ 1 và 2 trừ đi 2 lần phần diện tích chung là hình chữ nhật có độ dài 2 cạnh là 1cm; 3cm:

S_tp = 38 + 14 – 2. 3.1 = 46 cm²

Bài 31 trang 115 Toán 8 Tập 2: Điền số thích hợp vào ô trống ở bảng sau:

	Lăng trụ 1	Lăng trụ 2	Lăng trụ 3
Chiều cao của lăng trụ đứng tam giác	5 cm	7 cm
Chiều cao của tam giác đáy			5 cm
Cạnh tương ứng với đường cao của tam giác đáy	3 cm	5 cm
Diện tích đáy	6 cm2		15 cm2
Thể tích lăng trụ đứng		49 cm3	0,045 l

Lời giải:

Gọi chiều cao của tam giác đáy là h và chiều cao của lăng trụ là h₁.

Ta có :

$S=\frac{1}{2}a.h\Rightarrow h=\frac{2S}{a};a=\frac{2S}{h}V=S.h_1\Rightarrow S=\frac{V}{h_1};h_1=\frac{V}{S}$

+ Lăng trụ 1:

$h=\frac{2S}{a}=\frac{2.6}{3}=4cmV=S.h_1=6.5=30c{m}^3$

+ Lăng trụ 2:

$S=\frac{V}{h_1}=\frac{49}{7}=7c{m}^{2}h=\frac{2S}{a}=\frac{2.7}{5}=\frac{14}{5}cm$

+ Lăng trụ 3: đổi 0,045 (lít) = 0,045dm³ = 45cm³

^{$h_1=\frac{V}{S}=\frac{45}{15}=3cma=\frac{2S}{h}=\frac{2.15}{3}=10cm$}

Từ đó ta có bảng sau:

	Lăng trụ 1	Lăng trụ 2	Lăng trụ 3
Chiều cao của lăng trụ đứng tam giác	5 cm	7 cm	3 cm
Chiều cao của tam giác đáy	4 cm	$\frac{14}{5}$cm	5 cm
Cạnh tương ứng với đường cao của tam giác đáy	3 cm	5 cm	10 cm
Diện tích đáy	6 cm2	7 cm2	15 cm2
Thể tích lăng trụ đứng	30 cm3	49 cm3	0,045 l

Bài 32 trang 115 Toán 8 Tập 2: Hình 112b biểu diễn một lưỡi rìu bằng sắt, nó có dạng một lăng trụ đứng, BDC là một tam giác cân.

a) Hãy vẽ thêm nét khuất, điền thêm chữ vào các đỉnh rồi cho biết AB song song với những cạnh nào?

b) Tính thể tích lưỡi rìu.

c) Tính khối lượng của lưỡi rìu, biết khối lượng riêng của sắt là 7,874 kg/dm³ (phần cán gỗ bên trong lưỡi rìu là không đáng kể).

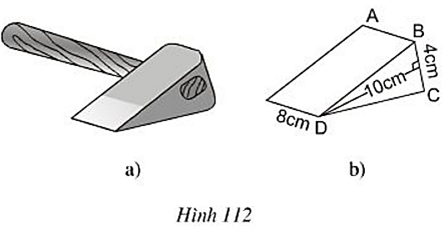
Lời giải:

a) Vẽ thêm nét khuất, ta được hình sau. Cạnh AB song song với những cạnh FC, ED.

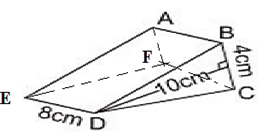
b) Diện tích đáy là: 

$S=\frac{1}{2}.4.10=20c{m}^2$

Thể tích lưỡi rìu:

V = S.h = 20. 8 = 160cm^3.

 c) Đổi 160cm³ = 0,16dm³

Khối lượng của lưỡi rìu là:

m = D.V = 7,874.0,16 1,26 kg

Bài 33 trang 115 Toán 8 Tập 2: Hình 113 là một lăng trụ đứng, đáy là hình thang vuông.

Hãy kể tên:

a) Các cạnh song song với cạnh AD.

b) Cạnh song song với cạnh AB.

c) Các đường thẳng song song với mặt phẳng (EFGH).

d) Các đường thẳng song song với mặt phẳng (DCGH).

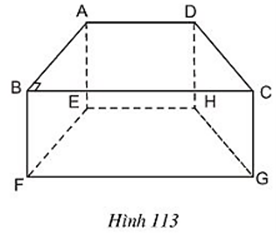
Lời giải:

a) Các cạnh song song với cạnh AD là EH, BC, FG.

b) Các cạnh song song với cạnh AB là EF.

c) Các đường thẳng song song với mặt phẳng (EFGH) là: AD, BC, AB, CD.

d) Các đường thẳng song song với mặt phẳng (DCGH): AE, BF.

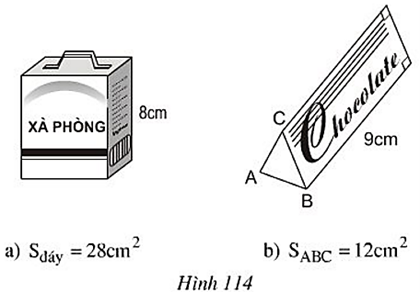
Bài 34 trang 116 Toán 8 Tập 2: Tính thể tích của hộp xà phòng và hộp sô-cô-la trên hình 114, biết:

a) Diện tích đáy hộp xà phòng là 28cm² (h.114a).

b) Diện tích tam giác ABC ở hình 114b là 12cm².

Lời giải:

a) Thể tích của hộp xà phòng là:

V = S.h = 28.8 = 224 (cm³)

b) Thể tích của hộp sô- cô – la là:

V = S.h = 12.9 = 108 cm³

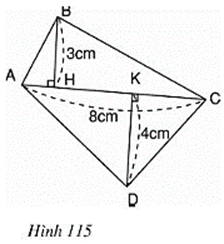
Bài 35 trang 116 Toán 8 Tập 2: Đáy của một lăng trụ đứng là tứ giác, các kích thước cho theo hình 115. Biết chiều cao của lăng trụ là 10cm. Hãy tính thể tích của nó.

Lời giải:

Nhận xét: Diện tích đáy của lăng trụ chính là diện tích của tứ giác ABCD.

Ta có:  S_ABCD = S_ABC + S_ADC

$=\frac{1}{2}AC.BH+\text{\hspace{0.17em}\hspace{0.17em}}\frac{1}{2}AC.DK=\frac{1}{2}\mathrm{.8.3}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{1}{2}\mathrm{.8.4}=28c{m}^2$

Thể tích của lăng trụ là: V = S.h = 28. 10 = 280 (cm³).