Giải SGK Toán 8 Bài 6: Giải bài toán bằng cách lập phương trình

Giải bài tập Toán lớp 8 Bài 6: Giải bài toán bằng cách lập phương trình

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 24 Toán 8 Tập 2: Giả sử hằng ngày bạn Tiến dành x phút để tập chạy. Hãy viết biểu thức với biến x biểu thị:

a) Quãng đường Tiến chạy được trong x phút, nếu chạy với vận tốc trung bình là 180m/ph.

b) Vận tốc trung bình của Tiến (tính theo km/h), nếu trong x phút Tiến chạy được quãng đường là 4500m.

Lời giải

a) Quãng đường Tiến chạy được là:

S = vt = 180x (m)

b) Đổi 4 500m = 4,5km.

x phút =  $\frac{x}{60}$giờ.

Vận tốc trung bình của Tiến là: 

v = $\frac{S}{t}$= $4,5:\text{\hspace{0.17em}\hspace{0.17em}}\frac{x}{60}=\frac{270}{x}(\text{}km/h)$.

Câu hỏi 2 trang 24 Toán 8 Tập 2: Gọi x là số tự nhiên có hai chữ số (ví dụ x = 12). Hãy lập biểu thức biểu thị số tự nhiên có được bằng cách:

a) Viết thêm chữ số 5 vào bên trái số x (ví dụ 12 → 512, tức là 500 + 12);

b) Viết thêm chữ số 5 vào bên phải số x (ví dụ 12 → 125, tức là 12 10 + 5).

Lời giải

a) Số tự nhiên mới khi viết thêm chữ số 5 vào bên trái chữ số tự nhiên cũ là: 5.100 + x

b) Số tự nhiên mới khi viết thêm chữ số 5 vào bên phải chữ số tự nhiên cũ là: 10x + 5

Câu hỏi 3 trang 25 Toán 8 Tập 2: Giải bài toán trong Ví dụ 2 bằng cách chọn x là số chó.

Lời giải

Gọi số x là chó, với điều kiện x là số nguyên dương và nhỏ hơn 36

Khi đó, số chân chó là 4x

Vì cả gà và chó là 36 con nên số gà là 36 – x và số chân gà là 2(36 – x)

Tổng số chân là 100 nên ta có phương trình:

4x + 2(36 – x) = 100

⇔ 4x + 72 – 2x = 100

⇔ 2x = 28

⇔ x = 14 (thỏa mãn các điều kiện của ẩn)

Vậy số chó là 14(con)

⇒ Số gà là: 36 – 14 = 22(con)

Bài tập (trang 25; 26)

Bài 34 trang 25 Toán 8 Tập 2: Mẫu số của một phân số lớn hơn tử số của nó là 3 đơn vị. Nếu tăng cả tử và mẫu của nó thêm 2 đơn vị thì được phân số mới bằng $\frac{1}{2}$. Tìm phân số ban đầu.

Lời giải:

Gọi x là tử số của phân số $(x\in \mathbb{Z};x\ne -3)$

Vì mẫu hơn tử số 3 đơn vị nên mẫu số là: x + 3.

Phân số ban đầu là $\frac{x}{x+3}$

Nếu tăng cả tử và mẫu của nó thêm 2 đơn vị thì được phân số mới là

$\frac{x+\text{\hspace{0.17em}}2}{x+3+2}=\frac{x+2}{x+\text{\hspace{0.17em}\hspace{0.17em}}5}\text{v}$

Theo giả thiết ta có: $\frac{x+\text{\hspace{0.17em}}2}{x+\text{\hspace{0.17em}}5}=\frac{1}{2}$

Suy ra: 2(x + 2) = 1.(x + 5)

$\iff$ 2x +  4 = x + 5

$\iff$x = 1 ( thỏa mãn điều kiện)

Vậy phân số ban đầu là $\frac{1}{4}$.

Bài 35 trang 25 Toán 8 Tập 2: Học kì một, số học sinh giỏi của lớp 8A bằng $\frac{1}{8}$ số học sinh cả lớp. Sang học kì hai, có thêm 3 bạn phấn đấu trở thành học sinh giỏi nữa, do đó số học sinh giỏi bằng 20% số học sinh cả lớp. Hỏi lớp 8A có bao nhiêu học sinh?

Lời giải:

Gọi số học sinh của lớp 8A là x (x ∈ N*; x > 3).

Số học sinh giỏi của học kì I là : $\frac{1}{8}x$   ( học sinh)

Sang học kì 2, số học sinh giỏi bằng 20% số học sinh cả lớp nên số học sinh giỏi của học kì II là :  

$20\%x=\frac{20}{100}x=\frac{1}{5}x$

Vì số học sinh giỏi của học kì II nhiều hơn số HSG của học kì I 3 học sinh nên ta có phương trình:

$\frac{1}{5}x-\frac{1}{8}x=3\iff \frac{8x-5x}{40}=\frac{120}{40}\iff 8x-5x=120$

$\iff$3x = 120

 $\iff x=40$(thỏa mãn điều kiện).

Vậy lớp 8A có 40 học sinh.

Bài 36 trang 26 Toán 8 Tập 2: (Bài toán nói về cuộc đời nhà toán học Đi-ô-phăng, lấy trong Hợp tuyển Hy Lạp – Cuốn sách gồm 46 bài toán về số, viết dưới dạng thơ trào phúng).

Thời thơ ấu của Đi – ô – phăng chiếm $\frac{1}{6}$ cuộc đời, $\frac{1}{12}$ cuộc đời tiếp theo là thời thanh niên sôi nổi. Thêm $\frac{1}{7}$ cuộc đời nữa của ông sống độc thân. Sau khi lập gia đình được 5 năm thì sinh một con trai.Nhưng số mệnh chỉ cho con sống bằng nửa đời cha. Ông đã từ trần 4 năm sau khi con trai mất. Đi- ô- phăng sống bao nhiêu tuổi. Hãy tính cho ra?

Lời giải:

Gọi x là số tuổi của ông Đi – ô – phăng (x > 0, x ∈ ).

Thời thơ ấu của ông là $\frac{1}{6}x$ ( uổi)

Thời thanh niên là $\frac{1}{12}x$ (tuổi)

Thời gian ông sống độc thân $\frac{1}{7}x$ (tuổi).

Thời gian lập gia đình đến khi có con và mất là $5+\frac{1}{2}x+\text{\hspace{0.17em}\hspace{0.17em}}4$.

Ta có phương trình:

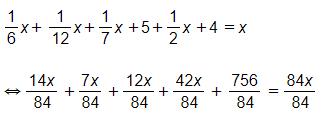
$\iff$14x + 7x + 12x + 42x + 756 = 84x

$\iff$-9x = -756

$\iff$x = 84 (thỏa mãn điều kiện).

Vậy nhà toán học Đi-ô-phăng thọ 84 tuổi.