Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tóm tắt tài liệu
Bộ đề thi học kì 2 môn toán lớp 8 bao gồm trắc nghiệm, tự luận và lời giải chi tiết
Trường THCS An Hòa
Đề khảo sát chất lượng học kì II
Môn toán lớp 8
Phần I : Trắc nghiệm (3,0 điểm)
Hãy chọn chỉ 1 chữ cái đứng trước câu trả lời đúng.
Câu 1: Phương trình 5(x + 1) – 2 = 3x – 5 có nghiệm là giá trị nào dưới đây:
A. 1
B. – 4
C. 4
D. 1
Câu 2: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
A. -2x +3= 0
B. x2 +3x – 2=0
C. 0. x – 5 =0
D. x(2x – 1 )=0
Câu 3: Phương trình 3x (2x + 3) = 2(2x + 3) có tập nghiệm là:
A. \(S = {\rm{\{ }}\frac{3}{2};\frac{{ – 2}}{3}{\rm{\} }}\)
B. \(S = {\rm{\{ }}\frac{3}{2};\frac{2}{3}{\rm{\} }}\)
C. \(S = {\rm{\{ – }}\frac{3}{2};\frac{2}{3}{\rm{\} }}\)
D. S= { -1 ; 1}
Câu 4: Phương trình 2x+k= x-1 nhận x = 2 là nghiệm khi
A. k = 3
B. k =- 3
C. k = 0
D. k = 1
Câu 5: Điều kiện xác định của phương trình \(\frac{{5x + 3}}{{x – 2}} = \frac{{2x}}{{{x^2} – 4}} – \frac{{2x + 3}}{x}\) là:
A. \(x \ne 0;x \ne 2\)
B. \(x \ne 2;x \ne – 2\)
C. \(x \ne 0;x \ne – 2\)
D. \(x \ne 0;x \ne \pm 2\)
Câu 6: Nếu \(x \le y\)thì:
A. a>b
B. \(a \le b\)
C. a<b
D. \(a \ge b\)
Câu 8. x =1 là một nghiệm của bất phương trình
A. x+5 < -13
B. \(\frac{x}{2} + 1 > 5x\)
C. 4x – 1>3 + x
D. \(\frac{x}{3} + 1 > – x\)
Câu 9. Bất phương trình: \(\frac{{15x + 2}}{4} > 1 + 3x\) có nghiệm là:
A. x<1
B. x<2
C. x > 2
D. Một kết quả khác
Câu 10. Phương trình |2x+5| – 3= x có nghiệm là :
A. \[{\rm{\{ }} – 2;\frac{{13}}{3}{\rm{\} }}\]
B. \[{\rm{\{ }} – 2;\frac{{ – 157}}{3}{\rm{\} }}\]
C. \[{\rm{\{ }} – 2;\frac{8}{3}{\rm{\} }}\]
D. \[{\rm{\{ }} – 2; – \frac{8}{3}{\rm{\} }}\]
Câu 11. Tam giác ABC vuông tại A có độ dài hai cạnh góc vuông lần lượt là 4cm và 5cm. Diện tích của tam giác ABC là:
A. 10 cm2
B. 20 cm2
C. 34 cm2
D. 18 cm2
Câu 12. Cho hình vẽ biết DE // BC và độ dài các đoạn
thẳng như hình vẽ. Khi đó \(\frac{{AE}}{{EC}}\)bằng:
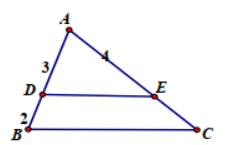
A. \(\frac{3}{2}\)
B. \(\frac{2}{3}\)
C. \(\frac{4}{5}\)
D. \(\frac{4}{3}\)
Câu 13. Cho ∆ABC có AB=14cm , AC=21 cm . AD là phân giác của góc A.
Biết BD = 8cm .Độ dài cạnh DC là :
A. 16/3cm
B. 12cm
C. 20 cm
D. 298/3 cm
Câu 14: Tam giác MNP đồng dạng với tam giác ABC theo tỉ số k = 1/ 2. Biết AB = 10BC = 14cm, độ dài đoạn thẳng là MN là
A. 7cm
B. 5cm
C. 28 cm
D. 20cm
Câu 15. Cho \(\Delta ABC\) và \(\Delta HIK\)có \(\frac{{AB}}{{IH}} = \frac{{AC}}{{HK}}\). Để \(\Delta ABC\) đồng dạng với \(\Delta HIK\) cần thêm điều kiện là:
A. \(\angle A = \angle I\)
B. \(\angle A = \angle H\)
C.\(\angle B = \angle I\)
D. \(\angle C = \angle K\)
Phần II : Tự luận (7,0 điểm)
Bài 1 (1 điểm): Giải các phương trình sau:
a) 3(x – 5) -2( 2x – 1) = 7 – 2x
b) \(\frac{2}{{x + 1}} – \frac{1}{{x – 2}} = \frac{{3x – 11}}{{(x + 1)(x – 2)}}\)
Bài 2 (1 điểm): Giải các phương trình sau:
a. Giải bất phương trình \(\frac{{3(x – 1)}}{4} + 1 \le \frac{{x + 2}}{3}\)
b. Cho \(A = \frac{{x – 5}}{{x – 8}}\). Tìm giá trị của x để A dương.
Bài 3 (1,5 điểm): Giải bài toán bằng cách lập phương trình.
Một phân số có tổng của tử và mẫu là 15. Nếu giảm tử đi 5 đơn vị và tăng mẫu thêm 2 đơn vị thì đươc phân số mới bằng 1/5. Tìm phân số ban đầu.
Bài 4 (3 điểm):
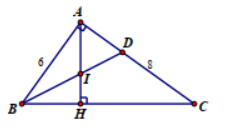
1. Cho tam giác ABC vuông ở A, AB = 6, AC = 8; đường cao AH, phân giác BD. Gọi I là giao điểm của AH và BD.
a. Tính AD, DC.
b. Chứng minh AB.BI = BD.HB và tam giác AID cân.
c. Chứng minh \(\frac{{IH}}{{IA}} = \frac{{AD}}{{DC}}\)
2. Một hình hộp chữ nhật có ba kích thước 3cm, 4cm và 6cm. Tính diện tích toàn phần của hình hộp chữ nhật.
Bài 5 (1 điểm): Tìm x; y thỏa mãn phương trình sau:
a) Cho a, b là các số dương. Chứng minh rằng:\(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}\)
b) Cho a,b,c là độ dài 3 vạnh của một tam giác. Chứng minh rằng:
\(\frac{1}{{a + b – c}} + \frac{1}{{b + c – a}} + \frac{1}{{c + a – b}} \ge \frac{1}{a} + \frac{1}{b} + \frac{1}{c}\)
Trường THCS An Hòa
Đáp án đề KSCL học kì II
Môn toán 8 năm học 2018-2019
|
Câu |
Nội dung |
Điểm |
||||||||||||||||||||||||||||||
|
I. Trắc nghiệm (3đ) |
|
0.2×15 |
||||||||||||||||||||||||||||||
|
II. Tự luận Bài 1( 1 điểm) |
a. Biến đổi về dạng:
|
0.25×2 |
||||||||||||||||||||||||||||||
|
b. – Tìm ĐKXĐ: \(x \ne – 1;x \ne 2\) – Quy đồng khử mẫu đúng: 2(x-2) – (x+1) = 3x-11 |
0.25×2 |
|||||||||||||||||||||||||||||||
|
Bài 2( 1 điểm) |
\(\frac{{3(x – 1)}}{4} + 1 \le \frac{{x + 2}}{3} \Leftrightarrow \frac{{9(x – 1) + 12}}{{4.3}} \le \frac{{4(x + 2)}}{{3.4}}\) a. \( \Leftrightarrow 9x – 9 + 12 \le 4x + 8\) \( \Leftrightarrow 5x \le 5 \Leftrightarrow x \le 1\) Vậy tập nghiệm của phương trình là:\[{\rm{\{ }}x/x \le 1\} \] |
0.25×2 |
||||||||||||||||||||||||||||||
|
b. Để A dương thì \(\frac{{x – 5}}{{x – 8}} > 0 \Leftrightarrow \left\{ \begin{array}{l}x – 5 < 0\\x – 8 < 0\end{array} \right.(1)\)hoặc \(\left\{ \begin{array}{l}x – 5 > 0\\x – 8 > 0\end{array} \right.(2)\) Giải (1): \(\left\{ \begin{array}{l}x – 5 < 0\\x – 8 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 5\\x < 8\end{array} \right. \Leftrightarrow x < 5\) Giải (2):\(\left\{ \begin{array}{l}x – 5 > 0\\x – 8 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 5\\x > 8\end{array} \right. \Leftrightarrow x > 8\) Vậy x < 5 hoặc x > 8 thì A dương. |
0.25×2 |
|||||||||||||||||||||||||||||||
|
Bài 3 (1 đ) |
– Chọn ẩn và ĐK đúng: Gọi x là mẫu của phân số phải tìm (ĐK: x∈Z, x≠ 0) – Biểu diễn các ĐL qua ẩn, lập PT đúng:\(\frac{{10 – x}}{{x + 2}} = \frac{1}{5}\) – Giải PT đúng: x = 8 – Trả lời |
0.25
0.25
0.25 0.25 |
||||||||||||||||||||||||||||||
|
Bài 4 (3 đ) |
a.Tính AD, DC – Tính BC = 10 cm – Lập tỉ số \(\frac{{AD}}{{DC}} = \frac{{AB}}{{BC}} \Rightarrow \frac{{AD}}{{DC + AD}} = \frac{{AB}}{{BC + AB}}\) Thay số, tính: AD = 3cm, DC = 5cm
|
0.5
0.5
0.25 |
||||||||||||||||||||||||||||||
|
b. – Chứng minh – Vậy \(\Delta AID\)cân – Lập tỉ số \(\frac{{IH}}{{IA}} = \frac{{HB}}{{AB}}\) |
0.25
0.5 |
|||||||||||||||||||||||||||||||
|
– Chứng minh – Suy ra: \(\frac{{IH}}{{IA}} = \frac{{AD}}{{DC}}\) |
0.5 |
|||||||||||||||||||||||||||||||
|
2. Diện tích toàn phần của hình hộp chữ nhật là: 2.(3+4).5 + 2.4.3 = 94cm2 |
0.5 |
|||||||||||||||||||||||||||||||
|
Bài 5 (1 đ) |
a. Với a, b>0, Xét hiệu \(\frac{1}{a} + \frac{1}{b} – \frac{4}{{a + b}} = \frac{{b(a + b) + a(a + b) – 4ab}}{{ab(a + b)}}\) \( = \frac{{{a^2} + {b^2} – 2ab}}{{ab(a + b)}} = \frac{{{{(a – b)}^2}}}{{ab(a + b)}} \ge 0\) Dấu = xảy ra khi a = b. Vậy: \(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}\) |
0.5 |
Xem thêm