Bộ 26 Đề thi Học kì 2 Toán lớp 8 năm 2022 – 2023 tải nhiều nhất

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 1

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 1)

Bài 1. (1,0 điểm)

Cho hình hộp chữ nhật ABCD.A’B’C’D’. Đường thẳng AA’ vuông góc với các mặt phẳng nào?

Bài 2. (3,0 điểm) Giải các phương trình sau:

a) 3x \( – \) 9 = 0;  

b) 2x² + 5x = 0;    

c) \(\left| {x – 3} \right| = 9 – 2x\).

Bài 3. (2,0 điểm) Một người đi xe máy từ A đến B hết 2 giờ và từ B về A hết 1 giờ 48 phút. Tính vận tốc của xe máy lúc đi từ A đến B, biết vận tốc lúc về lớn hơn vận tốc lúc đi là 4km/h.

Bài 4. (3,0 điểm) Cho tam giác ABC vuông tại A, đường cao AH.

a) Chứng minh $∆$ABC ~ $∆$HBA.

b) Chứng minh AB² = BH.BC.

c) Tia phân giá của góc ABC cắt AH, AC theo thứ tự tại M và N.

Chứng minh \(\frac{{MA}}{{MH}} = \frac{{NC}}{{NA}}\).

Bài 5. (1,0 điểm) Tìm tất cả các cặp số (x; y) thỏa mãn:

2010x² + 2011y² \( – \) 4020x + 4022y + 4021 = 0

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 2

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 2)

Phần I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm):

          Chọn chữ cái đứng trước câu trả lời đúng nhất cho mỗi câu hỏi sau và ghi vào giấy làm bài. Ví dụ câu 1 chọn đáp án C thì ghi là 1C.

Câu 1: Phương trình \[x = 3\] tương đương với phương trình nào sau đây?

A. \[2x =  – 6\].

B. \[2x = 6\].

C. \[x =  – 3\].

D. \[ – 2x = 6\].

Câu 2: Điều kiện xác định của phương trình  \[\frac{2}{x} + \frac{1}{{x – 6}} = 3\] là

A. \[x \ne 0\] và \[x \ne 6\].

B. \[x \ne 6\].

C. \[x \ne 0\].

D. \[x \ne 0\] và \[x \ne  – 6\].

Câu 3: Phương trình \[\left( {{\rm{2x}} – {\rm{5}}} \right).\left( {{\rm{x}} – {\rm{7}}} \right) = 0\] có tập hợp nghiệm là

A. \(S = \left\{ { – \frac{5}{2};\,\,7} \right\}\).

B. \(S = \left\{ {\frac{5}{2};\,\,7} \right\}\).

C. \(S = \left\{ {\frac{2}{5};\,\,7} \right\}\).

D. \(S = \left\{ {\frac{{ – 5}}{2};\,\, – 7} \right\}\).

Câu 4: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?

A. \[x + \frac{2}{3} \le 0\].

B. \[0x + \frac{1}{2} > 0\]..

C. \[{x^2} > \frac{1}{4}\].

D. \[\frac{1}{x} + 2 < 0\].

Câu 5: Bất phương trình \[2x – 4 > 0\]có nghiệm là

A. \[x > 4\].

B. \[x >  – 4\].

C. \[x >  – 2\].

D. \[x > 2\].

Câu 6: Rút gọn biểu thức \[A = \left| {3 – x} \right| + 5x – 8\] khi \[x < 3\] ta được A bằng

A. \[4x – 5\].

B. \[4x – 11\].

C. \[6x – 11\].

D. \[6x – 5\].

Câu 7: Mẹ cho Hiếu số tiền vừa đủ mua 4 gói bánh, giá 5000 đồng mỗi gói. Hiếu gặp một Tổ chức từ thiện đang quyên góp nhằm ủng hộ đồng bào bị lũ lụt. Hiếu quyết định ủng hộ x% số tiền mình đang có (x < 100). Biểu thức nào sau đây biểu thị số tiền Hiếu còn lại để đi mua bánh?

A. \[20\,000 – \frac{x}{5}\].

B. \[20\,000 – 200x\].

C. \[20 – \frac{x}{5}\].

D. \[20 – \frac{x}{{100}}\].

*Quan sát hình 1 và thực hiện các câu hỏi:  8;  9; 10.

Biết MN//BC; AD là đường phân giác của tam giác AMN; AM = 6cm; MB = 3cm; BC =9cm.

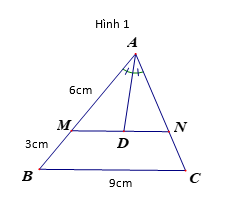
Câu 8: Tỉ số \(\frac{{DN}}{{DM}}\) bằng tỉ số

 

A. \(\frac{{DN}}{{DM}}\). C. \(\frac{{AM}}{{AN}}\).

B. \(\frac{{AM}}{{DN}}\). D. \(\frac{{AN}}{{AM}}\).

Câu 9: Tỉ số \(\frac{{AN}}{{NC}}\) bằng tỉ số

A. \(\frac{{AM}}{{AB}}\).

B. \(\frac{{AN}}{{AC}}\).

C. \(\frac{{AM}}{{MB}}\).

D. \(\frac{{MN}}{{BC}}\).

 

Câu 10: Độ dài đoạn thẳng MN là

A.\[4,5cm\].

B.\[6dm\].

C.\[6cm\].

D.\[3cm\].

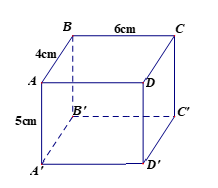
*Quan sát hình 2 và thực hiện các câu hỏi: 11; 12; 13; 14.

 Biết \[ABCD.\,A’B’C’D’\] là hình hộp chữ nhật có

  AB = 4cm; BC = 6cm; \[{\rm{AA’}}\]= 5cm.

Câu 11: Đường thẳng CD song song với đường thẳng   

A. \[AA’\]. C. \[AB\].

B. \[DD’\]. D. \(B’C’\).

Câu 12: Đường thẳng \[CC’\] song song với mặt phẳng

A. \[\left( {AA’B’B} \right)\]. C. \[\left( {A’B’C’D’} \right).\]

B.\[\left( {AA’C’C} \right)\]. D. \[\left( {ABCD} \right).\]

Câu 13: Mặt phẳng \[\left( {CC’D’D} \right)\] vuông góc với mặt phẳng

A. \[\left( {AA’B’B} \right).\]

B. \[\left( {A’B’C’D’} \right).\]

C. \[\left( {BB’D’D} \right).\]

D. \[\left( {AA’C’C} \right).\]

Câu 14: Một hộp thủy tinh dạng hình hộp chữ nhật, trong lòng có các kích thước như hình 2 thì có thể chứa tối đa bao nhiêu lít nước?

A. 120 lít

B.12 lít

C.0,12 lít

D.1,2 lít

Câu 15: Hình lập phương có diện tích toàn phần là 294cm² thì có thể tích là

A. \[343c{m^3}.\]

B. \[49c{m^3}.\]

C. \[294c{m^3}.\]

D. \[2401c{m^3}.\]

Phần II. TỰ LUẬN (5,0 điểm):

Câu 1. (1,5 điểm)

a.      Giải phương trình sau: \[4x – 2 = 3x – 5.\]

b.     Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số: \[4x – 1 < 8.\]

Câu 2. (1,0 điểm)

a.      Cho biết \[x > y,\] chứng tỏ rằng \[ – 5x – 2019\,\, < \,\, – 5y – 2019\].

b.     Giải phương trình sau: \[\frac{{x – 2003}}{{16}} + \frac{{x – 1997}}{{11}} + \frac{{x – 1992}}{9} + \frac{{x – 1991}}{7} = 10.\]

Câu 3. (2,5 điểm)

Cho tam giác nhọn DEF, hai đường cao EM và FN cắt nhau tại I.

a. Chứng minh hai tam giác DME và DNF đồng dạng;

b. Chứng minh \[IM.\,IE = IN.\,{\rm{IF}}\];

c.      Cho biết \[\widehat {EDF} = {45^0}\]. Chứng tỏ rằng \[{\left( {\frac{{MN}}{{{\rm{EF}}}}} \right)^2} = \frac{1}{2}.\]

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 3

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 3)

Câu 1. (2,0 điểm)

1) Phân tích các đa thức sau thành nhân tử:

a) \[5\left( {x – y} \right) – y\left( {x – y} \right)\]

b) \[{x^2} – 6x – {y^2} + 9\]

2) Cho \[m > n\]. Chứng tỏ rằng \[2012m – 2013 > 2012n – 2013\].

Câu 2. (3,0 điểm)

1) Giải các phương trình sau:

     a) \[7x + 35 = 0\]

     b) \[\frac{{8 – x}}{{x – 7}} – 8 = \frac{1}{{x – 7}}\]

2) Giải bất phương trình: \[18 – 3x\left( {1 – x} \right) \le 3{x^2} + 3x\]

Câu 3. (1,5 điểm)

     Năm nay, tuổi bố gấp 10 lần tuổi Nam. Bố Nam tính rằng sau 24 năm nữa tuổi bố chỉ còn gấp 2 lần tuổi Nam. Hỏi năm nay Nam bao nhiêu tuổi ?

Câu 4. (3,0 điểm)

Cho tam giác ABC có AD là đường phân giác xuất phát từ đỉnh A. Gọi E và F lần lượt là hình chiếu của B và C trên đường thẳng AD. Chứng minh rằng:

1) Tam giác ABE đồng dạng với tam giác ACF.

2) DE . CD = DF . BD

3) Biết \(\frac{{{\rm{AB}}}}{{{\rm{AC}}}}{\rm{ = }}\frac{{\rm{2}}}{{\rm{3}}}\) và diện tích tam giác BED bằng 24 cm². Tính diện tích tam giác CFD.

Câu 5. (0,5 điểm)

Tính giá trị của biểu thức \[A = \frac{{\left( {{1^4} + 4} \right)\left( {{5^4} + 4} \right)\left( {{9^4} + 4} \right) \cdots \left( {{{41}^4} + 4} \right)}}{{\left( {{3^4} + 4} \right)\left( {{7^4} + 4} \right)\left( {{{11}^4} + 4} \right) \cdots \left( {{{43}^4} + 4} \right)}}\].

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 4

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 4)

Bài 1 (3 điểm): Giải các phương trình và bất phương trình sau:

a) (x – 4)(x – 3)(x + 2) = 0;

b) |x – 3| = 12 – 2x;

c) \(\frac{1}{{x – 1}} – \frac{2}{{2 – x}} = \frac{5}{{(x – 1)(x – 2)}}\);

d) \[\frac{{x – 5}}{5} < \frac{{x – 7}}{3}\].

Bài 2 (2 điểm): Giải bài toán bằng cách lập phương trình.

Một đội máy kéo dự định mỗi ngày cày được 50 ha. Khi thực hiện mỗi ngày đội cày được 60 ha. Vì vậy đội không những đã hoàn thành xong trước kế hoạch 1 ngày mà còn cày thêm được 20 ha nữa. Tính diện tích ruộng mà đội phải cày theo kế hoạch.

Bài 3 (3 điểm): Cho hình chữ nhật ABCD có AB = 8 cm, BC = 6 cm. Gọi H là chân đường vuông góc kẻ từ A xuống BD, phân giác của BCD cắt BD ở E.

a) Chứng minh: Tam giác AHB đồng dạng tam giác BCD.

b) Chứng minh AH . ED = HB . EB.

c) Tính diện tích tứ giác AECH.

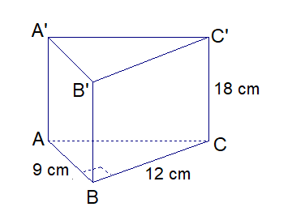
Bài 4 (1,5 điểm): Một hình lăng trụ đứng có đáy là tam giác vuông (như hình vẽ). Độ dài hai cạnh góc vuông của đáy là 9 cm, 12cm, chiều cao của lăng trụ là 1 8cm. Tính diện tích xung quanh và thể tích của hình lăng trụ đó.

Bài 5 (0,5 điểm): Tìm x, y thỏa mãn phương trình sau:

x² − 4x + y² − 6y + 15 = 2.

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 5

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 5)

Bài 1 (2,5 điểm): Giải phương trình và bất phương trình sau:

a)     \(2.\left( {3x – 1} \right) – 3x = 10\)        

b) \[\frac{{x + 1}}{x} + 1 = \frac{{3x – 1}}{{x + 1}} + \frac{1}{{x\left( {x + 1} \right)}}\]                   

c) \[\frac{{2x + 1}}{3} – \frac{{3x – 2}}{2} > \frac{1}{6}\]

Bài 2 (2,5 điểm):

Cho biểu thức \(A = \left( {\frac{{{x^2} – 3}}{{{x^2} – 9}} + \frac{1}{{x – 3}}} \right):\frac{x}{{x + 3}}\) (ĐKXĐ: \(x \ne 0,\) \(x \ne  \pm 3\))

a)     Rút gọn A

b)    Tìm các giá trị của x để \(\left| A \right| = 3\)

Bài 3 (2 điểm): Giải bài toán bằng cách lập phương trình

     Một đội thợ mỏ lập kế hoạch khai thác than, theo đó mỗi ngày phải khai thác 40 tấn than. Nhưng khi thực hiện, mỗi ngày đội khai thác được 45 tấn than. Do đó đội đã hoàn thành kế hoạch trước 2 ngày và còn vượt mức 10 tấn than. Hỏi theo kế hoạch đội phải khai thác bao nhiêu tấn than.

Bài 4 (4,5 điểm):

    Cho hình chữ nhật ABCD có AD = 6cm; AB = 8cm; hai đường chéo AC và BD cắt nhau tại O. Qua D kẻ đường thẳng d vuông góc với BD, d cắt tia BC tại E.

a)     Chứng minh rằng: \(\Delta BDE\) đồng dạng với \(\Delta DCE\)

b)    Kẻ \(CH \bot DE\) tại H. Chứng minh rằng: \(D{C^2} = CH.DB\)

c)     Gọi K là giao điểm của OE và HC. Chứng minh K là trung điểm của HC và tính tỉ số diện tích của \(\Delta EHC\) và diện tích của \(\Delta EDB.\)

Bài 5 (0,5 điểm): Cho tích \(a.b.c = 1\) và \(a + b + c > \frac{1}{a} + \frac{1}{b} + \frac{1}{c}.\)

Chứng minh rằng: \(\left( {a – 1} \right).\left( {b – 1} \right).\left( {c – 1} \right) > 0.\)

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 6

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 6)

  I. TRẮC NGHIỆM : (3 điểm)

Chọn chữ cái đứng trước câu trả lời em cho là đúng nhất ghi vào giấy làm bài:

Câu 1.  Phương trình nào sau đây là phương trình bậc nhất một ẩn ?

A. 0x + 2 = 0        

B. \(\frac{x}{{x – 3}} – \frac{{x – 1}}{x} = 1\)        

C. x + y = 0          

D. \(\frac{x}{{x – 3}} – \frac{{x – 1}}{x} = 1\)                       

Câu 2: Điều kiện xác định của phương trình \(\frac{x}{{x – 3}} – \frac{{x – 1}}{x} = 1\) là:

A. x\( \ne \)0                 

B. x\( \ne \)3                  

C.  x\( \ne \)0 và x\( \ne \)3                 

D. x\( \ne \)0 và x\( \ne \)-3         

Câu 3: Nghiệm của bất phương trình 4–2x < 6 là:

A.  x >– 5             

B. x <– 5              

C.  x < –1                       

D.  x >–1

Câu 4: Hình sau biểu diễn tập nghiệm của bất phương trình nào? 

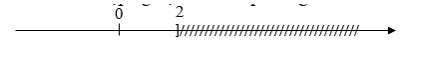
A. x $\le$ 2;     

B. x > 2 ;    

C. x  $\ge$ 2          

D. x <2 

Câu 5:  Nếu $∆$M^’N^’P^’ đồng dạng $∆$DEF thì ta có tỉ lệ thức nào đúng nhất nào:

A. \[\frac{{M’N’}}{{DE}} = \frac{{M’P’}}{{DF}}\]                 

B. \[\frac{{M’N’}}{{DE}} = \frac{{N’P’}}{{EF}}\].        

C.  \[\frac{{N’P’}}{{DE}} = \frac{{{\rm{EF}}}}{{M’N’}}\].               

D. \[\frac{{M’N’}}{{DE}} = \frac{{N’P’}}{{{\rm{EF}}}} = \frac{{M’P’}}{{DF}}\]

Câu 6: Dựa vào hình vẽ bên, hãy cho biết x =  ?                              

      

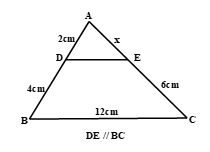
A. 9cm.

B. 6cm.                                   

C. 1cm.      

D. 3cm.

II. TỰ LUẬN (7 điểm)

Bài 1: (2,5 điểm):

1. Giải phương trình: (3x – 2)(4x + 5) = 0

2. Giải bất phương trình sau và biểu diễn tập hợp nghiệm trên trục số: \(\frac{{2x – 3}}{2} > \frac{{8x – 11}}{6}.\)

Bài 2: (1,5 điểm): Một người đi xe máy từ Đắk Lắk đến Đăk Nông với vận tốc trung bình 50km/h. Khi về người đó đi với vận tốc 45km/h nên thời gian về nhiều hơn thời gian đi là 16 phút. Tính độ dài quãng đường Đắk Lắk – Đắk Nông  và thời gian đi và về.

Bài 3: (3 điểm)

Cho tam giác ABC vuông tại A,  AB = 8cm, AC = 6cm, AD là tia phân giác góc A, \[{\rm{D}} \in {\rm{BC}}\]

a. Tính \(\frac{{{\rm{DB}}}}{{{\rm{DC}}}}\).

b. Kẻ đường cao AH (\[{\rm{H}} \in {\rm{BC}}\]). Chứng minh rằng: \({\rm{\Delta AHB}}\) đồng dạng \({\rm{\Delta CHA}}\).

c.Tính  \(\frac{{{{\rm{S}}_{\Delta {\rm{AHB}}}}}}{{{{\rm{S}}_{\Delta {\rm{CHA}}}}}}\)

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 7

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 7)

Bài 1 (2 điểm): Cho \[A = \frac{x}{{{x^2} – 4}} + \frac{1}{{x + 2}} – \frac{2}{{x – 2}}\,\,:\,\,1 – \frac{x}{{x + 2}}\] (x ≠ ± 2)

a) Rút gọn A.

b) Tính giá trị của A khi x = − 4.

c) Tìm các giá trị nguyên của x để A có giá trị là số nguyên.

Bài 2 (2,5 điểm): Giải các phương trình và bất phương trình sau:

a) 2x + 3 = 5x – 6;

b) \(\left( {\frac{2}{{{x^2} + 1}} – 3} \right)\,\,.\,\,\frac{{x – 1}}{{2x – 3}} =  – 2\);

c) \[1 – \frac{{2x – 5}}{6} > \frac{{3 – x}}{4}\].

Bài 2 (2 điểm): Giải bài toán bằng cách lập phương trình.

Trong tháng Giêng hai tổ công nhân may được 800 chiếc áo. Tháng Hai, tổ một vượt mức 15%, tổ hai vượt mức 20%. Do đó, cả hai tổ sản xuất được 945 cái áo. Hỏi trong tháng Hai mỗi tổ may được bao nhiêu chiếc áo?

Bài 4 (2,5 điểm): Cho tam giác nhọn ABC, có AB = 12cm, AC = 15 cm. Trên các cạnh AB và AC lấy các điểm D và E sao cho AD = 4 cm, AE = 5cm.

a) Chứng minh DE // BC. Từ đó suy ra: ∆ADE đồng dạng với ∆ABC.

b) Từ E kẻ EF // AB (F thuộc BC). Tứ giác BDEF là hình gì?

Từ đó suy ra: ∆CEF đồng dạng với ∆EAD.

c) Tính CF và FB. Biết BC = 18 cm.

Bài 5 (1 điểm): Tính thể tích của một hình lăng trụ đứng có đáy là tam giác vuông, chiều cao của lăng trụ là 9 cm. Độ dài hai cạnh góc vuông của đáy là 4 cm và 5 cm.

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 8

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 8)

Bài 1 (2,5điểm). Giải các phương trình:

a) \[2x–7 = 5x + 20\]     

b) \[{x^3} – 4x = 0\;\]

c) \(\frac{1}{{2x – 3}} – \frac{3}{{2{x^2} – 3x}} = \frac{5}{x}\)          

d) \(\left| {{x^2} – 1} \right| = 2x + 1\)

Bài 2 (1,5 điểm). Giải các bất phương trình:

a) \[3x – 5\; \le x + 1\]

b) \(\frac{{2x – 2}}{3} > 2 – \frac{{x + 2}}{2}\)

Bài 3 (1,5 điểm). 

Một ôtô đi từ thành phố Hồ Chí Minh đến Phan Thiết với vận tốc 60km/h. Khi trở về cũng trên tuyến đường đó, ôtô chạy với vận tốc 40km/h nên thời gian về mất nhiều hơn thời gian đi là 2 giờ 10 phút. Tính quãng đường từ thành phố Hồ Chí Minh đến Phan Thiết?

Bài 4 (3,5 điểm).

1) Cho hình chữ nhật ABCD. Kẻ AH \[ \bot \]BD (H \[ \in \]BD).

a) Chứng minh: \[\Delta HDA\] đồng dạng với\[\Delta ADB\]

b) Chứng minh: AD² = DB.HD

c) Tia phân giác của góc ADB cắt AH và AB lần lượt tại M và K. Chứng minh: \[AK.AM = BK.HM\]

  d) Gọi O là giao điểm của AC và BD. Lấy P thuộc AC, dựng hình chữ nhật AEPF

(EÎAB, FÎAD). BF cắt DE ở Q. Chứng minh rằng: EF//DB và 3 điểm A, Q, O thẳng hàng.

2) Tính thể tích hình hộp chữ  nhật ABCD.EFGH biết cạnh AE = 5cm; EH = 4cm; AB = 3cm.

Bài 5 (1 điểm).

a) Cho các số a, b, c thỏa mãn: a + b + c = \(\frac{3}{2}\). Chứng minh rằng: a² + b² + c²\( \ge \)\(\frac{3}{4}\).

b) Tìm giá trị nhỏ nhất của biểu thức P = x² + 2y² + 2xy – 6x – 8y + 2028.

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 9

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 9)

Bài 1 (3 điểm): Giải các phương trình và bất phương trình sau:

a) 4(3x + 4)² – 3(3x + 4);

b) \(\frac{3}{{2x}} – \frac{{x – 6}}{{2{x^2} – 4x}} = 4\)

c) \[\frac{x}{2} + \frac{{3 – 2x}}{5} \ge \frac{{3x – 5}}{6}\].

Bài 2 (2 điểm): Giải bài toán bằng cách lập phương trình.

Một phòng họp có 100 ghế nhưng lại có 144 người đến họp. Do đó người ta phải kê thêm hai dãy ghế và mỗi dãy tăng thêm hai ghế. Tính số dãy ghế ban đầu trong phòng.

Bài 4 (3 điểm): Cho ΔABC có AB = 8cm, AC = 12cm. Trên cạnh AB lấy điểm D sao cho BD = 2cm, trên cạnh AC lấy điểm E sao cho AE = 9cm

a) Tính các tỉ số \(\frac{{{\rm{AE}}}}{{{\rm{AD}}}}{\rm{;}}\,\,\frac{{{\rm{AD}}}}{{{\rm{AC}}}}\).

b) Chứng minh: ΔADE đồng dạng với ΔABC.

c) Đường phân giác của \(\widehat {BAC}\) cắt BC tại I. Chứng minh: IB . AE = IC . AD.

Bài 5 (1,5 điểm): Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 12 cm, AD = 16 cm, AA’ = 15 cm. Tính diện tích toàn phần và thể tích hình hộp chữ nhật.

Bài 5 (0,5 điểm): Giải phương trình:

(2020 – x)³ + (2021 – x)³ + (2x – 4041)³ = 0.

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 10

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 10)

Bài 1 (3 điểm): Giải các phương trình và bất phương trình sau:

a) 2x + 3 = 2 – 5x;

b) \(\frac{{5x – 3}}{{x + 2}} – 4 = \frac{{ – 10}}{{x + 2}}\);

c) \[\frac{{8x – 3}}{2} + 2 \ge \frac{{3x – 5}}{4}\].

Bài 2 (2 điểm): Giải bài toán bằng cách lập phương trình.

Một chiếc thuyền đi từ bến A đến bến B hết 6 giờ, từ bến B đến bến A hết 8 giờ. Hỏi một đám bèo trôi theo dòng sông từ A đến B hết bao lâu?

Bài 3 (2,5 điểm): Cho hình thang ABCD vuông tại A và D có đường chéo DB vuông góc với cạnh bên BC tại B, biết AD = 3 cm, AB = 4 cm.

a) Chứng minh ΔABD đồng dạng với ΔBDC.

b) Tính độ dài DC.

c) Gọi E là giao điểm của AC với BD. Tính diện tích tam giác AED.

Bài 4 (2 điểm): Cho hình hộp chữ nhật ABCD.A^’B^’C^’D^’ có AB = 12 cm, BC = 15 cm, AA^’ = 18 cm.

a) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật.

b) Tính độ dài đường chéo AC^’ của hình hộp chữ nhật (làm tròn đến chữ số thập phân thứ nhất).

Bài 5 (0,5 điểm): Cho x² + y² + z² = 200. Tìm giá trị nhỏ nhất của biểu thức:

M = 2xy − yz − zx.

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 11

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 11)

Câu 1 (2,0 điểm). Giải các phương trình sau:

a) \[8x – 4 = 0\]     

b) \(\frac{{x – 4}}{3} = 4 – \frac{{4 – 3x}}{5}\)

c) \[\frac{4}{{x + 1}} – \frac{1}{x} = \frac{{{x^2} – 1}}{{{x^2} + x}}\]        

d) \[\left| {5 – x} \right| + 3x = 1\]

Câu 2 (2,0 điểm).

Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:

a) \( – 3x + 12 \ge 0\)

b) \(\frac{{x + 1}}{2} – 1 < \frac{{2x – 1}}{3}\)

Câu 3 (2,0 điểm).

1) Tìm giá trị x nguyên nhỏ nhất  để  giá trị của biểu thức \((x + 1)(x – 2)\) không nhỏ hơn giá trị của biểu thức \({(x – 2)^2} – 1\).

2) Giải bài toán sau bằng cách lập phương trình:

Anh Việt đi xe máy từ Hải Dương đến Thái Nguyên với vận tốc trung bình 40 km/h. Cùng lúc đó, anh Nam cũng đi từ Hải Dương đến Thái Nguyên bằng ô tô với vận tốc trung bình 50km/h. Anh Nam đến Thái Nguyên trước anh Việt 30 phút. Tính quãng đường từ Hải Dương đến Thái Nguyên.

Câu 4 (3,0 điểm). Cho DABC có ba góc nhọn. Kẻ các đường cao AD, BE, CF chúng cắt nhau tại H. Chứng minh rằng: 

a) $∆$AEB đồng dạng $∆$AFC.      

b) AD.HB = AB.DF.

c) DA là phân giác của \(\widehat {EDF}\). 

Câu 5 (1,0 điểm).

a) Phân tích đa thức sau thành nhân tử: \({x^3} + {y^3} + {z^3} – 3xyz\).

b) Cho 3 số a, b, c thỏa mãn \[a + b + c\; \ne 0\]. Chứng minh rằng :

\(\frac{{{a^3} + {b^3} + {c^3} – 3abc}}{{a + b + c}} \ge 0\).

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 12

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 12)

Bài 1 (2,5 điểm): Giải các phương trình và bất phương trình sau:

a) \(\frac{{5x – 2}}{3} + x = 1 + \frac{{5 – 3x}}{2}\);

b) (x +2)(3 – 4x) = x² + 4x + 4;

c) 3(x – 2)(x + 2) < 3x² + x.

Bài 2 (2 điểm):

a) Tìm x sao cho giá trị của biểu thức \(\frac{{2{x^2} – 3x – 2}}{{{x^2} – 4}}\) bằng 2.

b) Tìm x sao cho giá trị của hai biểu thức \(\frac{{6x – 1}}{{3x + 2}}\) và \(\frac{{2x + 5}}{{x – 3}}\) bằng nhau.

Bài 3 (2 điểm): Giải bài toán bằng cách lập phương trình.

Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất 50 sản phẩm. Khi thực hiện, mỗi ngày tổ sản xuất được 57 sản phẩm.Do đó tổ đã hoàn thành trước kế hoạch 1 ngày và còn vượt mức 13 sản phẩm. Hỏi theo kế hoạch, tổ phải sản xuất bao nhiêu sản phẩm?

Bài 4 (2,5 điểm): Cho hình thang cân ABCD có AB // DC và AB < DC, đường chéo BD vuông góc với cạnh bên BC. Vẽ đường cao BH.

a) Chứng minh ∆BDC đồng dạng với ∆HBC.

b) Cho BC = 15 cm, DC = 25 cm. Tính HC và HD.

c) Tính diện tích hình thang ABCD.

Bài 5 (1 điểm): Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông, biết độ dài hai cạnh góc vuông là 3 cm và 4 cm; chiều cao của lăng trụ là 10 cm. Hãy tính diện tích toàn phần của hình lăng trụ.

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 13

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 13)

I. TRẮC NGHIỆM (3.0 điểm) Hãy khoanh tròn vào chữ cái in hoa trước câu trả lời đúng.

Câu 1: Phương trình nào sau đây là phương trình bậc nhất một ẩn?

A.  \(15{x^2} + 4 = 3\)

B. \(4y – 8 = 0\)

C.  \(\frac{3}{7}x\, – \frac{2}{9} = 0\)

D. \(\frac{{15}}{x} + 3 = 0\)

Câu 2: Trong các phương trình sau phương trình nào tương đương với phương trình: \(2x – 4 = 0\)?

     A.  \(x – 2 = 0\)            B.  \(4x – 2 = 0\)

C.  \( – \,4x + 8 = 0\)         D. \(2x + 4 = 0\)

Câu 3:  Điều kiện xác định của phương trình \(\frac{{3x – 2}}{{x + 7}} = \frac{{6x + 1}}{{2x – 3}}\) là:

A.   \(x \ne  – 7\)               

B.   \(x \ne \frac{3}{2}\)               

C.    \(x \ne  – 7\) hoặc \(x \ne \frac{3}{2}\)           

D.   \(x \ne  – 7\) và \(x \ne \frac{3}{2}\)

Câu 4:  An có 60000 đồng, mua bút hết 15000 đồng, còn lại mua vở với giá mỗi quyển vở là 6000 đồng. Số quyển vở An có thể mua nhiều nhất là:

     A.   7 quyển                B.   8 quyển

C.    9 quyển                    D.   10 quyển

Câu 5: Tập nghiệm của phương trình \(\left| {2x – 5} \right| = 5\):            

A.   \(S = \left\{ 5 \right\}\)

B.   \(S = \left\{ { – 5} \right\}\)

C.    \(S = \left\{ {0\,;\,\,5} \right\}\)

D.    \(S = \left\{ { – 5\,;\,\,5} \right\}\)

Câu 6: Nếu \(a \le b\) thì:

 A.   \(5a\,\, \ge \,\,5b\)

B.   \( – \,\,4a\,\, \ge  – \,\,4b\)

C.    \(a\,\, – 8 \ge b\,\, – 8\)

D.   \(8 – a \ge 8 – b\)

Câu 7: Cho \(AB = \,15\,d\,m\,;\,\,\,\,CD = 5\,m\). Khi đó:

A.   \(\frac{{AB}}{{CD}} = \frac{3}{{10}}\)

B.   \(\frac{{CD}}{{AB}} = \frac{1}{3}\)

C.    \(\frac{{AB}}{{CD}} = 3\)

D.  \(\frac{{CD}}{{AB}} = \frac{3}{{10}}\)

Câu 8: Cho hình vẽ (hình bên): Biết \(MN//BC\), \(MN = 3\,cm\,;\,\,\,AM = 2\,cm,\,\,AB = 5\,cm\)

 Khi đó độ dài đoạn thẳng \(BC\) là

 

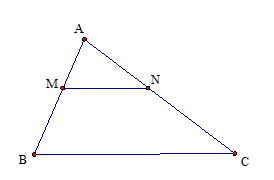
A. \(\frac{{10}}{3}\,cm\)  B. \[\frac{6}{5}cm\]

C. \(7,5\,cm\)                   D. \(5\,cm\)               

Câu 9: Ánh nắng mặt trời chiếu một cây phi lao ngã bóng trên mặt đất dài 6,4m. Cùng thời điểm đó một cái cọc cao 20cm cắm vuông góc với mặt đất có bóng đổ dài 32cm. Chiều cao của cây phi lao là:

  A.   \(10,24\,m\)             B.   \(4\,m\)

C.    \(2\,m\)                     D.     \(12,8\,m\)

Câu 10: Cho tam giác ABC, có AD là đường phân giác thì:

A. \(\frac{{AB}}{{AC}} = \frac{{DC}}{{BD}}\)

B. \(\frac{{AB}}{{BD}} = \frac{{DC}}{{AC}}\)

C. \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\)

D. \(\frac{{AC}}{{BD}} = \frac{{DC}}{{AB}}\)

Câu 11: Số cạnh của hình chóp lục giác đều là:

     A. 6                            B.   12

C.   18                             D. \(15\)

Câu 12: Một bể bơi có hình dạng một hình hộp chữ nhật, có kích thước bên trong của đáy lần lượt là 6m và 25m. Dung tích nước trong hồ khi mực nước trong hồ cao 2m là:

A.    \(150\,{m^3}\)          B.   \(170\,{m^3}\)

C. \(300\,{m^3}\) D. \(340\,{m^3}\)

II./ TỰ LUẬN (7điểm)

Bài 1: (2đ)

a) Giải phương trình sau:  \(\frac{{x + 1}}{{x – 2}} – \frac{5}{{x + 2}} = \frac{{12}}{{{x^2} – 4}} + 1\)

b) Giải phương trình sau: \(\left| {2x + 6} \right| – x = 3\)

c) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:   \(\frac{{2x + 2}}{5} + \frac{3}{{10}} < \frac{{3x – 2}}{4}\)

Bài 2: (1,5đ)

          Một ô tô đi từ Thanh Hoá đến Hà Nội với vận tốc 40km/h. Sau 2 giờ 15 phút nghỉ lại ở Thanh Hoá, ô tô lại từ Thanh Hoá về Hà Nội với vận tốc là 30km/h. Tính chiều dài quãng đường Hà Nội – Thanh Hoá  biết rằng tổng thời gian cả đi lẫn về là 11 giờ (kể cả thời gian nghỉ lại ở Thanh Hoá).

Bài 3: (3,5đ)

Cho tam giác ABC vuông tại A vẽ đường cao AH, AB = 6 cm, AC = 8cm

a/ Chứng minh  ∆HBA ~ ∆ABC  

b/ Tính BC , AH , BH.

c/ Gọi I và K lần lượt hình chiếu của điểm H lên cạnh AB, AC. Chứng minh AI.AB =AK.AC. 

 

Đề thi Học kì 2 Toán lớp 8 năm 2022 tải nhiều nhất (26 đề) – Đề 14

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề 14)

Bài 1 (2,5 điểm):  Giải các phương trình sau:

a) x + 3 = 9x – 25;

b) \[\frac{{2x – 1}}{{12}} – \frac{{3 – x}}{{18}} = \frac{{ – 1}}{{36}}\];

c) \[\frac{x}{{x + 11}} + \frac{3}{{x – 12}} = \frac{{ – 12x + 33}}{{\left( {x + 11} \right)\left( {x – 12} \right)}}\].

Bài 2 (1 điểm): Giải bất phương trình và biểu diễn tập hợp nghiệm trên trục số:

\[\frac{{x – 2}}{{10}} + \frac{{x – 5}}{{15}} > \frac{{10x – 1}}{{30}}\].

Bài 3 (2 điểm): Giải bài toán bằng cách lập phương trình.

Một ô tô chạy trên quãng đường AB. Lúc đi từ A đến B ôtô chạy với vận tốc 50 km/h, lúc về từ B đến A ô tô chạy với vận tốc 60 km/h. Vì vậy thời gian về ít hơn thời gian đi là \[\frac{1}{2}\] giờ. Tính độ dài quãng đường AB.

Bài 4 (3 điểm): Cho ∆ABC có ba đường cao AA’, BB’, CC’ cắt nhau tại H.

a) Chứng minh: ∆AB’B đồng dạng với ∆AC’C.

b) Chứng minh: ∆ABC đồng dạng với ∆AB’C’.

c) Chứng minh: \(\frac{{HA’}}{{AA’}} + \frac{{HB’}}{{BB’}} + \frac{{HC’}}{{CC’}} = 1\).

Bài 5 (1 điểm): Cho hình hộp chữ nhật ABCD.MNPQ có AB = 15 cm, AD = 20 cm và AM = 12 cm. Tính thể tích hình hộp chữ nhật ABCD.MNPQ.

Bài 6 (0,5 điểm): Giải phương trình sau: 

(x² + 9)(x² + 9x) = 22 (x – 1)².