50 Bài tập Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp (có đáp án)- Toán 8

Bài tập Toán 8 Chương 1 Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp

A. Bài tập Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp

Bài 1:  Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử)

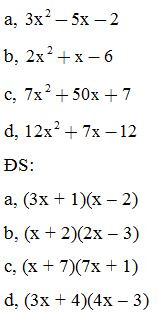
Bài 2: Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử)

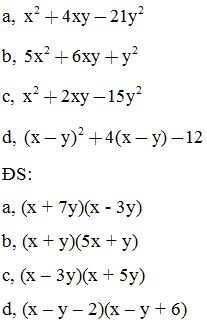
Bài 3: Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử)

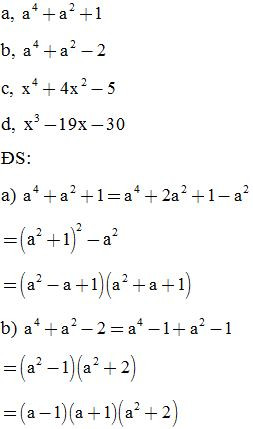
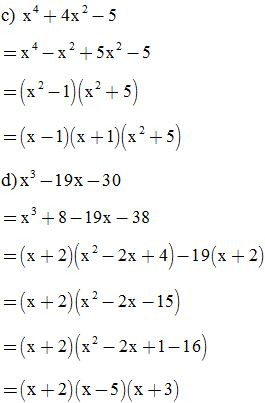
Bài 4: Phân tích các đa thức sau thành nhân tử: (thêm bớt cùng một hạng tử)

   

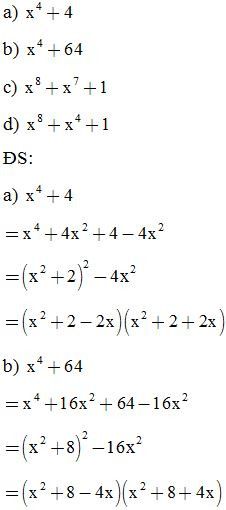
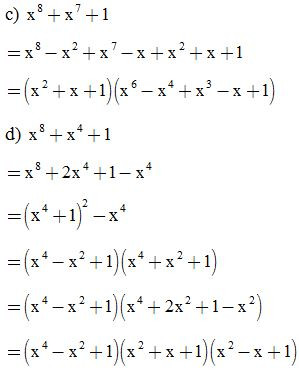
Bài 5: Phân tích các đa thức sau thành nhân tử: (đặt biến phụ)

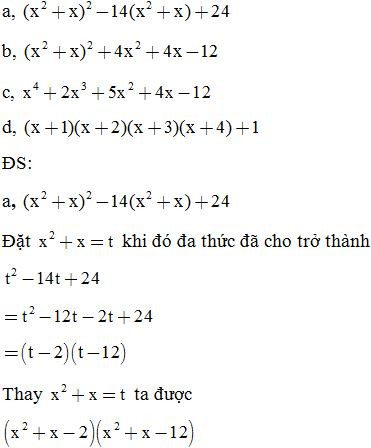
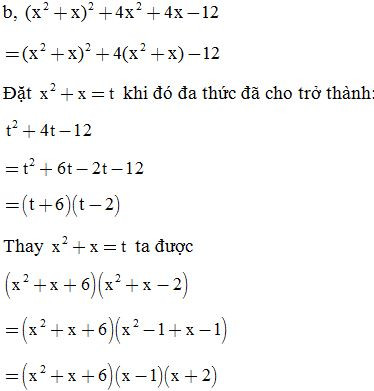
Bài 6: Phân tích các đa thức sau thành nhân tử: (đặt biến phụ)

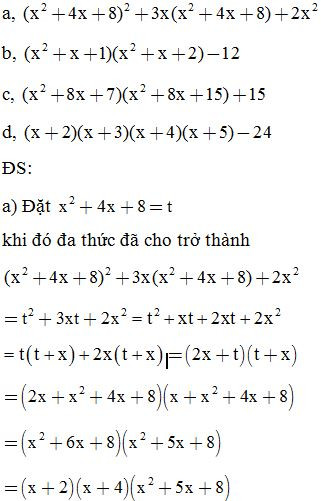
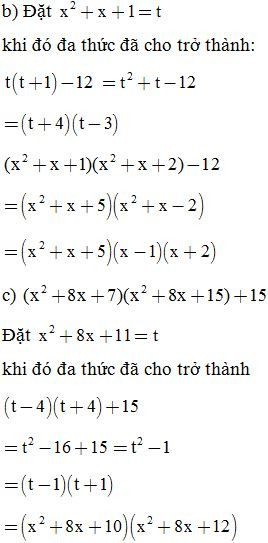
Bài 7: Tìm x biết:

a, $x^2–10x+16=0$

b, $x^2–11x–26=0$

c, $2x^2+7x–4=0$

ĐS:

a, x= 8, x = 2

b, x = -2, x =13

c, x = -4, x = $\frac{1}{2}$

Bài 8: Tìm x biết:

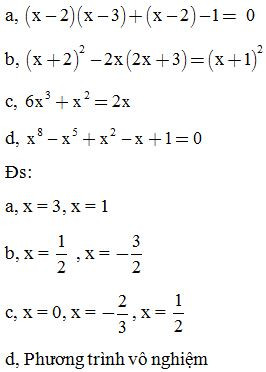
Bài 9: Chứng minh với mọi số nguyên n thì $A=n^4-2n^3-n^2+2n$ chia hết cho 24.

ĐS:

Gợi ý: $A=\left(n-2\right)\left(n^3-n\right)$$=\left(n-2\right)\left(n-1\right)n\left(n+1\right)$

A là tích của 4 số tự nguyên liên tiếp nên A chia hết cho 2, cho 3 và cho 4. Vì (2;3)=1 nên A chia hết cho 6. Suy ra A chia hết cho 4.6=24 

Bài 10: 

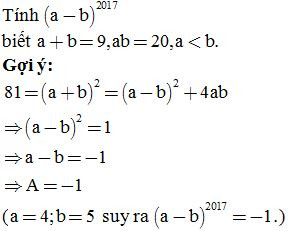
B. Lý thuyết Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp

Khái niệm: Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

 

Khi thực hiện phân tích đa thức thành nhân tử các biểu thức phức tạp ta thường sử dụng phối hợp cả ba phương pháp phân tích đa thức thành nhân tử cơ bản: phương pháp nhân tử chung, phương pháp hằng đẳng thức, phương pháp nhóm hạng tử.

Chú ý: Nếu các hạng tử của đa thức có nhân tử chung thì ta nên sử dụng phương pháp đặt nhân tử chung trước để đa thức trở lên đơn giản hơn rồi mới tiếp tục phân tích đến kết quả cuối cùng.

Xem thêm