Bài tập Toán 8 Chương 4 Bài 2: Liên hệ giữa thứ tự và phép nhân có đáp án
A. Bài tập Liên hệ giữa thứ tự và phép nhân
I. Bài tập trắc nghiệm
Bài 1: Trong các khẳng định sau đây, khẳng định nào sai?
( 1 ) ( – 4 ).5 ≤ ( – 5 ).4
( 2) ( – 7 ).12 ≥ ( – 7 ).11
( 3 ) – 4x2 > 0
A. ( 1 ),( 2 ) và ( 3 )
B. ( 1 ),( 2 )
C. ( 1 )
D. ( 2 ),( 3 )
Lời giải:
+ Ta có: ( – 4 ).5 = 4.( – 5 ) → Khẳng định ( 1 ) sai.
+ Ta có: 12 > 11 ⇒ 12.( – 7 ) < 11.( – 7 ) → Khẳng định ( 2 ) sai.
+ Ta có: x2 ≥ 0 ⇒ – 4x2 ≤ 0 → Khẳng định ( 3 ) sai
Chọn đáp án A.
Bài 2: Cho a + 1 ≤ b + 2. So sánh hai số 2a + 2 và 2b + 4 nào dưới đây đúng ?
A. 2a + 2 > 2b + 4
B. 2a + 2 < 2b + 4
C. 2a + 2 ≤ 2b + 4
D. 2a + 2 ≥ 2b + 4
Lời giải:
Với ba số a, b và c mà c > 0, ta có: Nếu a ≤ b thì ac ≤ bc
Khi đó, ta có: a + 1 ≤ b + 2 ⇒ 2( a + 1 ) ≤ 2( b + 2 ) ⇔ 2a + 2 ≤ 2b + 4.
Chọn đáp án C.
Bài 3: Cho a > b. Khẳng định nào sau đây đúng?
A. – 3a – 1 > – 3b – 1
B. – 3( a – 1 ) < – 3( b – 1 )
C. – 3( a – 1 ) > – 3( b – 1 )
D. 3( a – 1 ) < 3( b – 1 )
Lời giải:
+ Ta có: a > b ⇒ – 3a < – 3b ⇔ – 3a – 1 < – 3b – 1
→ Đáp án A sai.
+ Ta có: a > b ⇒ a – 1 > b – 1 ⇔ – 3( a – 1 ) < – 3( b – 1 )
→ Đáp án B đúng.
+ Ta có: a > b ⇒ a – 1 > b – 1 ⇔ – 3( a – 1 ) < – 3( b – 1 )
→ Đáp án C sai.
+ Ta có: a > b ⇒ a – 1 > b – 1 ⇔ 3( a – 1 ) > 3( b – 1 )
→ Đáp án D sai.
Chọn đáp án B.
Bài 4: Cho a ≥ b. Khẳng định nào sau đây đúng?
A. 2a – 5 ≤ 2( b – 1 )
B. 2a – 5 ≥ 2( b – 1 )
C. 2a – 5 ≥ 2( b – 3 )
D. 2a – 5 ≤ 2( b – 3 )
Lời giải:
+ Ta có: a ≥ b ⇒ 2a ≥ 2b
Mặt khác, ta có: – 5 ≥ – 6
Khi đó 2a – 5 ≥ 2b – 6 hay 2a – 5 ≥ 2( b – 3 ).
Chọn đáp án C.
Bài 5: Cho x > 0. Khẳng định nào sau đây đúng?
A. ( x + 1 )2 ≤ 0
B. ( x + 1 )2 > 1
C. ( x + 1 )2 ≤ 1
D. ( x + 1 )2 < 1
Lời giải:
Ta có: x > 0 ⇒ x + 1 > 1 ⇒ ( x + 1 )2 > 12.
Hay ( x + 1 )2 > 1.
Chọn đáp án B.
Bài 6: Cho tam giác ABC, khẳng định nào sau đây đúng?
Lời giải:
Chọn đáp án A
Bài 7: Cho a > b. So sánh: 2a + 10 và 2b + 9
A. 2a + 10 < 2b + 9
B. 2a +10 = 2b + 9
C. 2a + 10 > 2b + 9
D. Chưa thể kết luận
Lời giải:
* Ta có: a > b nên 2a > 2b
Suy ra: 2a + 9 > 2b + 9 (1)
* Lại có: 10 > 9 nên 2a + 10 > 2a + 9 (2)
Từ (1) và (2) suy ra: 2a+ 10 > 2b + 9
Chọn đáp án C
Bài 8: Cho -2a – 8 < – 2b – 8. So sánh a và b
A. a > b
B. a < b
C. a > b+1
D. a < b + 1
Lời giải:
Ta có: – 2a – 8 < – 2b – 8 nên: -2a – 8 + 8 < – 2b – 8 + 8 hay -2a < – 2b
Nhân cả 2 vế bất đẳng thức với – < 0 ta được: a > b
Chọn đáp án A
Bài 9: Cho a < b . Khi đó:
A. 2a – 3 < 2b + 4
B. – 2a – 3 < – 2b + 4
C. 2a + 3 < 2b – 4
D. – 2a + 1 < – 2b +2
Lời giải:
Ta có: a < b, nhân cả 2 vế bất đẳng thức với 2 > 0 ta được: 2a < 2b
Suy ra: 2a – 3 < 2b – 3 (1)
Lại có: -3 < 4 nên 2b – 3 < 2b + 4 (2)
Từ (1) và (2) suy ra: 2a – 3 < 2b + 4
Chọn đáp án A
Bài 10: Cho 4a < 7a . Khẳng định nào sau đây là đúng?
A. a < 0
B. 2a +1 < 1
C. a > 0
D. -3a > 0
Lời giải:
Ta có: 4a < 7a nên 4a + (-4a) < 7a + (- 4a) hay 0 < 3a (1)
Nhân cả 2 vế của bất đẳng thức (1) với > 0 ta được:
Vậy a > 0
Chọn đáp án C
II. Bài tập tự luận có lời giải
Bài 1: Cho a > b > 0. So sánh a2 và ab; a3 và b3
Lời giải
* Với a > b > 0 ta có:
+) a. a > a. b ⇔ a2 > ab
+) Ta có: a2 > ab ⇒ a2a> a. ab ⇔ a3 > a2b
Mà,
a > b > 0 ⇒ ab > b.b ⇔ ab > b2 ⇒ ab. a > b2. b ⇒ a2.b > b3.
⇒ a2b > b3 ⇒ a3 > a2b > b3
⇒ a3 > b3
Vậy a2 > ab và a3 > b3.
Bài 2: Cho a > b > 0. So sánh a3……b3, dấu cần điền vào chỗ chấm là?
Lời giải
* Với a > b > 0 ta có:
+) a. a > a. b ⇔ a2 > ab
+) Ta có: a2 > ab ⇒ a2. a > a. ab ⇔ a3 > a2b
Mà a > b > 0 ⇒ ab > b. b ⇔ ab > b2
⇒ ab. a > b2. b ⇒ a2b > b3.
⇒ a2b > b3 ⇒ a3 > a2b > b3.
⇒ a3 > b3
Vậy a3 > b3
Bài 3 Cho a, b bất kì. Chọn câu đúng?
Lời giải
Đáp án cần chọn là: C
Bài 4 Cho a, b bất kì. Chọn câu đúng nhất?
Lời giải
Xét hiệu: P = a2 + b2 – 2ab = (a – b)2 ≥ 0 (luôn đúng với mọi a, b)
Nên a2 + b2 > 2ab với mọi a, b.
Dấu “=” xảy ra khi a = b.
Đáp án cần chọn là: C
Bài 5 Cho -2018a < -2018b. Khi đó?
Lời giải
Bài 6 a) Nhân cả hai vế của bất đẳng thức -2 < 3 với 5091 thì được bất đẳng thức nào?
b) Dự đoán kết quả: Nhân cả hai vế của bất đẳng thức -2 < 3 với số c dương thì ta được bất đẳng thức nào?
Lời giải
a) – 2. 5091 = – 10 182 và 3. 5091 = 15 273
⇒ – 10 182 < 15 273
b) Nhân cả hai vế của bất đẳng thức -2 < 3 với số c dương thì ta được bất đẳng thức: -2c < 3c
Bài 8 Đặt dấu thích hợp (<, >) vào ô vuông:
a) (-15,2) . 3,5 …..(-15,08) . 3,5;
b) 4,15 . 2,2 ….. (-5,3) . 2,2.
Lời giải
a) (-15,2) . 3,5 < (-15,08) . 3,5
b) 4,15 . 2,2 > (-5,3) . 2,2
Bài 9
a) Nhân cả hai vế của bất đẳng thức -2 < 3 với -345 thì được bất đẳng thức nào?
b) Dự đoán kết quả: Nhân cả hai vế của bất đẳng thức -2 < 3 với số c âm thì ta được bất đẳng thức nào?
Lời giải
a) – 2 . (- 345) = 690; 3 . 345 = – 1035
⇒ 690 > – 1035
b) Nhân cả hai vế của bất đẳng thức -2 < 3 với số c âm thì ta được bất đẳng thức: -2c > 3c
Bài 10 Cho -4a > -4b, hãy so sánh a và b.
Lời giải
a < b
Bài 11 Khi chia cả hai vế của bất đẳng thức cho cùng một số khác không thì sao?
Lời giải
– Khi chia cả hai vế của bất đẳng thức cho cùng một số dương: Bất đằng thức không đổi dấu
– Khi chia cả hai vế của bất đẳng thức cho cùng một số âm: bất đằng thức đổi dấu
III. Bài tập vận dụng
Bài 1 Cho a < b, hãy so sánh:
2a và 2b; 2a và a + b; -a + b; -a và -b.
Bài 2 Số a là số âm hay dương nếu:
12a < 15 a? 4a < 3a? -3a > -5a?
Bài 3 Cho a < b, chứng tỏ:
a) 2a – 3 < 2b – 3; b) 2a – 3 < 2b + 5.
Bài 4 Cho tam giác ABC. Các khẳng định sau đúng hay sai?
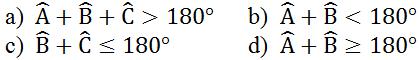
Bài 5
a) So sánh (-2).3 và -4,5.
b) Từ kết quả câu a) hãy suy ra các bất đẳng thức sau:
(-2).30 < -45; (-2).3 + 4,5 < 0
Bài 6 Cho a < b, chứng minh:
a) 3a + 1 < 3b + 1; b) -2a – 5 > -2b – 5
Bài 7 Chứng minh:
a) 4.(-2) + 14 < 4.(-1) + 14;
b) (-3).2 + 5 < (-3).(-5) + 5
c) a + 5 < b + 5;
d) – 3a > -3b
e) 5a – 6 ≥ 5b – 6;
g) -2a + 3 ≤ – 2b + 3
Bài 8 Cho a < b, hãy so sánh:
2a + 1 với 2b + 1; 2a + 1 với 2b + 3
Bài 9 Mỗi khẳng định sau đúng hay sai? Vì sao?
a)
b)
c)
d)
Bài 10 Số a là số âm hay dương nếu:
a)
b)
c)
B. Lý thuyết Liên hệ giữa thứ tự và phép nhân
1. Tính chất 1
– Khi nhân (hay chia) cả hai vế của bất đẳng thức với cùng một số dương ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
– Với ba số a, b, c trong đó c > 0, ta có:
+ Nếu a > b thì ac > bc;
+ Nếu a < b thì ac < bc;
+ Nếu a ≥ b thì ac ≥ bc;
+ Nếu a ≤ b thì ac ≤ bc.
2. Tính chất 2
– Khi nhân (hay chia) cả hai vế bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.
– Với ba số a, b, c trong đó c <0, ta có:
+ Nếu a > b thì ac < bc;
+ Nếu a < b thì ac > bc;
+ Nếu a ≥ b thì ac ≤ bc;
+ Nếu a ≤ b thì ac ≥ bc.
3. Tính chất bắc cầu
Nếu a > b và b > c thì a > c.
Tương tự cho các bất đẳng thức với dấu <; ≥; ≤.