50 Bài tập Hình hộp chữ nhật (tiếp) (có đáp án)- Toán 8

Bài tập Toán 8 Chương 4 Bài 2: Hình hộp chữ nhật (tiếp)

A. Bài tập Hình hộp chữ nhật (tiếp)

I. Bài tập trắc nghiệm

Bài 1: Cho hình hộp chữ nhật ABCD. A’B’C’D’. Có bao nhiêu đường thẳng song song với AA’.

A. 1    

B. 2

C. 3    

D. 4

Lời giải:

Do ABCD.A’B’C’D’ là hình hộp chữ nhật nên các mặt bên

(ABB’A’); (CBB’C’); (DCC’D’); (DAA’D’) là các hình chữ nhật

suy ra AA’// BB’// CC’// DD’

Chọn đáp án C

Bài 2: Cho hình lập phương ABCD.A’B’C’D’. Hỏi có bao nhiêu mặt phẳng song song với đường thẳng A’D’?

A. 1    

B. 2

C. 3    

D. 4

Lời giải:

Các mặt phẳng song song với đường thẳng A’D’ là mặt phẳng (BCC’B’) và mặt phẳng (ABCD)

Chọn đáp án B

Bài 3: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AD= 6cm và DD’ = 8cm. Tính BC’?

A. 10cm    

B. 9cm

C. 8cm    

D. 12cm

Lời giải:

Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên tứ giác ABCD ; DCC’D’ và CBB’C’ là hình chữ nhật

Suy ra: BC = AD = 6cm; CC’ = DD’ = 8cm

Áp dụng đinh lí Py ta go vào tam giác BCC’ ta có:

BC’² = BC² + CC’² = 6² + 8² = 100

Suy ra: BC’ = 10cm

Chọn đáp án A

Bài 4: Cho hình hộp chữ nhật ABCD.A’B’C’D’. Có bao nhiêu đường thẳng song song với BC’?

A. 0    

B.1

C.2    

D.3

Lời giải:

Ta có: AB // C’D’ ( // CD) và AB = C’D’ ( = CD)

Suy ra tứ giác ABC’D’ là hình bình hành

Suy ra: BC’// AD’

Chọn đáp án B

Bài 5: Cho hình lập phương ABCD.MNPQ có độ dài cạnh là 2cm. Tính tổng diện tích các mặt của hình lập phương?

A. 8cm²     

B. 12cm²

C. 20cm²    

D. 24cm²

Lời giải:

Hình lập phương đã cho gồm 6 mặt bằng nhau. Mỗi mặt là hình vuông có độ dài cạnh là 2cm

Diện tích mỗi mặt là: 2² = 4cm²

Tổng diện tích các mặt của hình lâp phương là: 4.6 = 24cm²

Chọn đáp án D

II. Bài tập tự luận có lời giải

Bài 1: Cho hình hộp chữ nhật ABCD. A’B’C’D’. Có bao nhiêu cạnh cắt cạnh AB

Lời giải

Có bốn cạnh cắt AB là AD, AA’, BC, BB’

Đáp án cần chọn là: A

Bài 2 Cho hình hộp chữ nhật ABCD. A’B’C’D’. Cạnh nào có thể cắt được cạnh AB

Lời giải

Có bốn cạnh cắt AB là AD, AA’, BC, BB’

Bài 3 Cho hình hộp chữ nhật ABCD. A’B’C’D’. Có bao nhiêu cạnh song song với AB?

Lời giải

Có ba cạnh song song với AB là A’B’, CD, C’D’.

Bài 4: Cho hình hộp chữ nhật ABCD. A’B’C’D’. Cạnh nào song song với A’D’?

Lời giải

Có ba cạnh song song với A’D’ là AD, BC, B’C’

Bài 5 Trong các mặt của một hình hộp chữ nhật, tính số căp mặt song song với nhau là

Lời giải

Có 3 cặp mặt phẳng song song là mp (ABB’A’) và mp (DC C’D’); mp (ABCD) và mp (A’B’C’D’); mp (ADD’A’) và mp (BCC’B’)

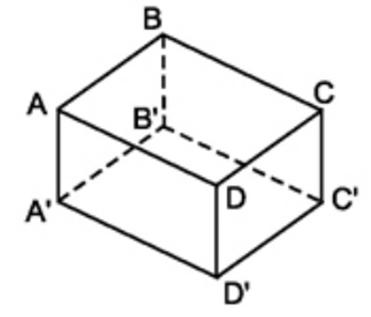
Bài 6 Quan sát hình hộp chữ nhật ABCD.A’B’C’D’ (h.71a). Hãy kể tên các mặt, các đỉnh và các cạnh của hình hộp chữ nhật.

Lời giải

– Các mặt: ABCD, A’B’C’D’, ABB’A’, CDD’C’, ADD’A’, BCC’B’

– Các đỉnh: A, B, C, D, A’, B’, C’, D’

– Các cạnh: AB, BC, CD, DA, A’B’, B’C’, C’D’, D’A’, AA’, BB’, CC’, DD’

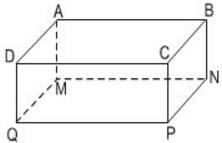
Bài 7 Hãy kể tên những cạnh bằng nhau của hình hộp chữ nhật ABCD.MNPQ (h.72).

Hình 72

Lời giải:

Trong hình hộp chữ nhật ABCD.MNPQ những cạnh bằng nhau là:

AB = CD = PQ = MN

AD = QM = PN = CB

DQ = AM = BN = CP

Bài 8 ABCD.A₁B₁C₁D₁ là một hình hộp chữ nhật (h.73).

a) Nếu O là trung điểm của đoạn CB₁ thì O có là điểm thuộc đoạn BC₁ hay không?

b) K là điểm thuộc cạnh CD, liệu K có thể là điểm thuộc cạnh BB₁ hay không?

Hình 73

Lời giải:

Với hình hộp chữ nhật ABCD.A₁B₁C₁D₁:

a) Nếu O là trung điểm của đoạn CB₁ thì O cũng là trung điểm của đoạn C₁B vì CBB₁C₁ là hình chữ nhật nên hai đường chéo có chung một trung điểm.

b) K là điểm thuộc cạnh CD thì K không thuộc cạnh BB₁ vì bốn điểm C, D, B, B₁ không thuộc một mặ

Bài 9 Các kích thước của hình hộp chữ nhật ABCD.A₁B₁C₁D₁ là DC = 5cm, CB = 4cm, BB₁ = 3cm. Hỏi độ dài DC₁ và CB₁ là bao nhiêu xentimet?

Lời giải:

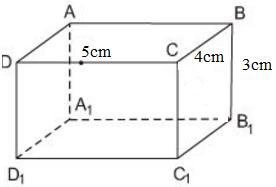
Vì ABCD.A₁B₁C₁D₁ là hình hộp chữ nhật

⇒ DCC₁D₁ và CBB₁C₁ là hình chữ nhật.

⇒ CC₁ = BB₁ = 3cm

ΔDCC₁ vuông tại C, áp dụng định lí Py-ta–go ta có:

DC₁² = DC² + CC₁²

ΔCBB₁ vuông tại B, áp dụng định lí Py–ta-go ta có:

CB₁²= CB² + BB₁²

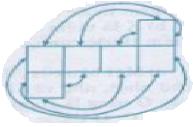
Bài 10 Xem hình 74a, các mũi tên hướng dẫn cách ghép các cạnh với nhau để có được một hình lập phương.

Hình 74

Hãy điền thêm vào hình 74b các mũi tên như vậy.

Lời giải:

Mỗi hình vuông tương ứng với một mặt của hình lập phương có 6 mặt. Đầu tiên chúng ta giữ cố định một hình vuông ở giữa để làm một mặt trong cùng của hình lập phương, sau đó di chuyển các hình vuông còn lại theo chiều mũi tên như sau để được hình lập phương:

Bài 11 Quan sát hình hộp chữ nhật ở hình 75:

– Hãy kể tên các mặt của hình hộp.

– BB’ và AA’ có cùng nằm trong một mặt phẳng hay không?

– BB’ và AA’ có điểm chung hay không?

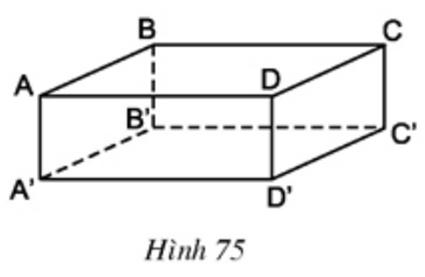
Lời giải

– Các mặt: ABCD, A’B’C’D’, ABB’A’, CDD’C’, ADD’A’, BCC’B’

– BB’ và AA’ có cùng nằm trong một mặt phẳng là ABB’A’

– BB’ và AA’ không có điểm chung

III. Bài tập vận dụng

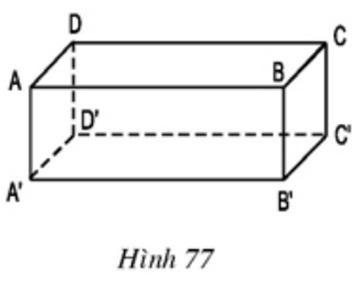
Bài 1 Quan sát hình hộp chữ nhật ở hình 77:

– AB có song song với A’B’ hay không? Vì sao?

– AB có nằm trong mặt phẳng (A’B’C’D’) hay không?

Bài 2 Tìm trên hình 77 các đường thẳng song song với mặt phẳng (A’B’C’D’).

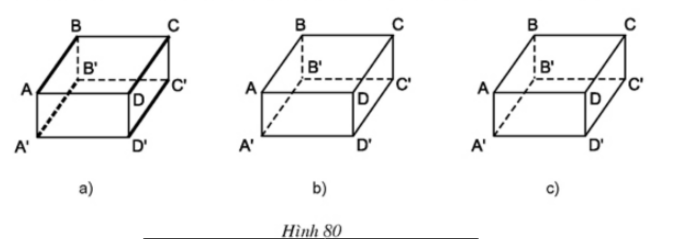
Bài 3 Người ta tô đậm những cạnh song song và bằng nhau của một hình hộp chữ nhật như ở hình 80a. Hãy thực hiện điều đó với hình 80b và 80c.

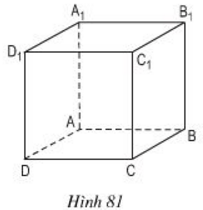
Bài 4 $ABCD.A_1{B}_1{C}_1{D}_1$ là một hình lập phương (h.81). Quan sát hình và cho biết:

a) Những cạnh nào song song với cạnh $C_{1}C$?

b) Những cạnh nào song song với $A_1{D}_1$?

Bài 5 Một căn phòng dài 4,5m, rộng 3,7m và cao 3,0m. Người ta muốn quét vôi trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là 5,8m2. Hãy tính diện tích cần quét vôi.

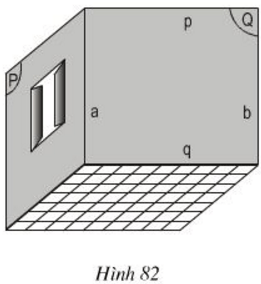
Bài 6 Hình 82 vẽ một phòng ở. Quan sát hình và giải thích vì sao:

a) Đường thẳng b song song với mp(P)?

b) Đường thẳng p song song với sàn nhà?

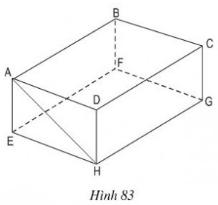
Bài 7 Hình hộp chữ nhật ABCD.EFGH (h.83) có cạnh AB song song với mp(EFGH).

a) Hãy kể tên các cạnh khác song song với mặt phẳng (EFGH).

b) Cạnh CD song song với những mặt phẳng nào của hình hộp chữ nhật?

c) Đường thẳng AH không song song với mặt phẳng (EFGH), hãy chỉ ra mặt phẳng song song với đường thẳng đó.

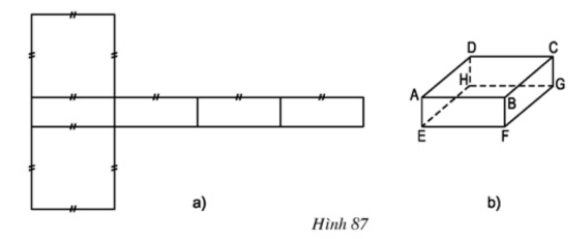
Bài 8

1) Gấp hình 87a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật hay không?

2) Kí hiệu các đỉnh hình hộp gấp được như 87b.

Bài 9

a) Đường thẳng BF vuông góc với những mặt phẳng nào?

b) Hai mặt phẳng (AEHD) và (CGHD) vuông góc với nhau, vì sao?

Bài 10

a) Tính các kích thước của một hình hộp chữ nhật, biết rằng chúng tỉ lệ với 3, 4, 5 và thể tích của hình hộp này là $480c{m}^3$

b) Diện tích toàn phần của một hình lập phương là $486c{m}^2$. Thể tích của nó bằng bao nhiêu?

B. Lý thuyết Hình hộp chữ nhật (tiếp)

1. Hai đường thẳng song song trong không gian

+ Hai đường thẳng a, b gọi là song song với nhau nếu chúng cùng nằm trong một mặt phẳng và không có điểm chung. Kí hiệu a // b.

+ Hai đường thẳng phân biệt, cùng song song với một đường thẳng thứ ba thì song song với nhau.

Chú ý: Hai đường thẳng phân biệt trong không gian có thể:

– Cắt nhau – Song song – Chéo nhau (không cùng nằm trong một mặt phẳng)

Ví dụ:

Cắt nhau: Chẳng hạn như AM và MN cắt nhau tại M, chúng cùng nằm trong mặt phẳng ( AMNB ),….

Song song: Chẳng hạn như DQ và CP song song với nhau, chúng cùng nằm trong mặt phẳng ( DQPC ),….

Chéo nhau: Chẳng hạn như AD và MN, chúng nằm ở hai mặt phẳng khác nhau

2. Đường thẳng song song với mặt phẳng. Hai mặt phẳng song song

a) Đường thẳng song song với mặt phẳng

– Một đường thẳng a gọi là song song với một mặt phẳng ( P ) nếu đường thẳng đó không nằm trong mặt phẳng ( P ) và song song với một đường thẳng d nằm trong mặt phẳng.

Kí hiệu a // ( P )

– Nếu một đường thẳng song song với một mặt phẳng thì chúng không có điểm chung.

 
 
 
 
 

•  
•  
•  
•  

 

b) Hai mặt phẳng song song

– Nếu mặt phẳng ( Q ) chứa hai đường thẳng cắt nhau, cùng song song với mặt phẳng ( P ) thì mặt phẳng ( Q ) song song với mặt phẳng ( P ). Kí hiệu ( Q )//( P ).

– Hai mặt phẳng song song với nhau thì không có điểm chung.

– Hai mặt phẳng phân biệt có một điểm chung thì chúng có chung một đường thẳng đi qua điểm chung đó (đường thẳng chung đó được gọi là giao tuyến của hai mặt phẳng).

c) Ví dụ áp dụng

Cho hình hộp chữ nhật như hình vẽ

Các đường thẳng song song với mặt phẳng như: MN//( ABCD ), PN//( AMQD ), …

Các mặt phẳng song song với nhau như: ( ABNM )//( DCPQ ),( BCPN )//( AMQD ), …