Bài tập Toán 8 Chương 4 Bài 5: Diện tích xung quanh của hình lăng trụ đứng
A. Bài tập Diện tích xung quanh của hình lăng trụ đứng
I. Bài tập trắc nghiệm
Bài 1: Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật, AB = 4cm BC = 5cm, chiều cao h = 2,5cm. Diện tích xung quanh của hình lăng trụ đứng là?
A. Sxq = 22,5( cm2 )
B. Sxq = 45( cm2 )
C. Sxq = 30( cm2 )
D. Sxq = 36( cm2 )
Lời giải:
Ta có chu vi của đáy là: p = 2( AB + BC ) = 2( 4 + 5 ) = 18( cm )
Khi đó: Sxq = p.h = 18.2,5 = 45( cm2 )
Chọn đáp án B.
Bài 2: Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật, AB = 4cm BC = 5cm, chiều cao h = 2,5cm. Diện tích toàn phần của hình lăng trụ đứng là?
A. Stp = 62,5( cm2 )
B. Sxq = 85( cm2 )
C. Stp = 70( cm2 )
D. Sxq = 76( cm2 )
Lời giải:
Theo câu 2, ta có: Sxq = 45( cm2 )
Khi đó ta có: Stp = Sxq + 2S = 45 + 2.4.5 = 85( cm2 )
Chọn đáp án B.
Bài 3: Cho hình lăng trụ đứng tam giác có độ dài ba cạnh đáy là 4 cm, 6cm và 8cm. Biết diện tích xung quanh bằng 90cm2. Tính chiều cao của hình lăng trụ?
A. 5cm
B. 6cm
C. 4cm
D. 8cm
Lời giải:
Chu vi đáy là: P = 4 + 6 + 8 = 18cm
Diện tích xung quanh của hình lăng trụ đứng
Sxq = P.h nên chiều cao:
Chọn đáp án A
Bài 4: Cho hình lăng trụ đứng có đáy là lục giác đều cạnh 6cm, chiều cao lăng trụ là 6cm. Tính diện tích xung quanh của hình lăng trụ?
A. 160cm2
B. 216cm2
C. 250cm2
D. 320cm2
Lời giải:
Do đáy của hình lăng trụ là lục giác đều cạnh 6cm nên chu vi đáy là:
P = 6.6 = 36cm
Diện tích xung quanh của hình lăng trụ là:
Sxq = P.h = 36.6 = 216 cm2
Chọn đáp án B
Bài 5: Cho hình lăng trụ đứng ABC.A’B’C’, AB = 6cm; AC = 8cm, AA’ = 5cm và diện tích xung quanh là 120cm2. Hỏi tam giác ABC là tam giác gì
A. Tam giác cân
B. Tam giác nhọn
C.Tam giác tù
D. Tam giác vuông
Lời giải:
Chọn đáp án D
Bài 6: Cho hình lăng trụ đứng ABCD.MNPQ có đáy ABCD là hình bình hành có AB = 6cm, BC = 4cm , AM = 5cm. Tính diện tích xung quanh của hình lăng trụ?
A. 100cm2
B. 120cm2
C. 150cm2
D. 200cm2
Lời giải:
Chu vi đáy là:
P = 2(AB + BC) = 2.(6 + 4) = 20cm
Diện tích xung quanh của hình lăng trụ đã cho là:
Sxq = Sd . h = 20. 5 = 100cm2
Chọn đáp án A
II. Bài tập tự luận có lời giải
Bài 1: Một hình hộp chữ nhật có kích thước của đáy là 10 cm và 15 cm. Biết diện tích xug quang bằng tổng diện tích hai đáy. Độ dài chiều cao là?
Lời giải
Đặt AA’ = x.
Diện tích xung quang bằng:
2 (10 + 15).x = 50x (cm2)
Tổng diện tích hai đáy bằng 2.10.15 = 300 (cm2)
Ta có 50x = 300 ⇔ x = 6
Vậy chiều cao bằng 6 cm.
Bài 2 Cho hình lăng trụ tam giác đều ABC. A’B’C’ có chiều cao bằng 2 cm, . Tính diện tích xung quang của hình lăng trụ.
Lời giải
Tam giác vuông ABB’ có nên là tam giác vuông cân tại B nên AB = BB’ = 2 cm.
Vì tam giác ABC đều nên chu vi bằng 3AB = 3.2 = 6 cm
Diện tích xung quanh bằng 6.2 = 12 (cm2)
Bài 3 Cho hình lăng trụ tam giác đều ABC. A’B’C’ có chiều cao bằng 2 cm, . Tính diện tích xung quanh của hình lăng trụ.
Lời giải
Tam giác vuông ABB’ có nên là tam giác vuông cân tại B nên AB = BB’ = 2 cm.
Vì tam giác ABC đều nên chu vi bằng 3AB = 3.2 = 6 cm
Diện tích xung quanh bằng 6.2 = 12 (cm2)
Bài 4: Hai mặt phẳng chứa hai đáy của một lăng trụ đứng có song song với nhau hay không?
– Các cạnh bên có vuông góc với hai mặt phẳng đáy hay không?
– Các mặt bên có vuông góc với hai mặt phẳng đáy hay không?
Lời giải
– Hai mặt phẳng chứa hai đáy của một lăng trụ đứng có song song với nhau
– Các cạnh bên có vuông góc với hai mặt phẳng đáy
– Các mặt bên có vuông góc với hai mặt phẳng đáy
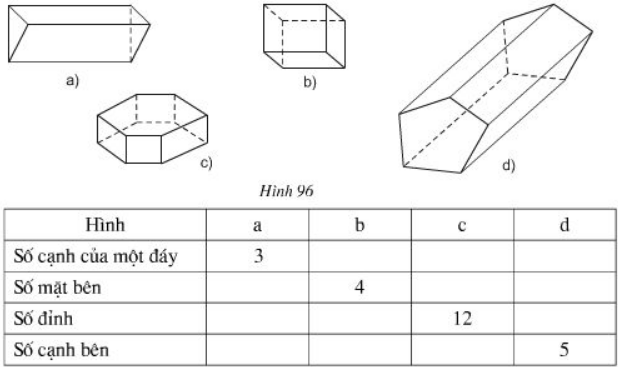
Bài 5 Quan sát các lăng trụ đứng trong hình 96 rồi điền số thích hợp vào các ô trống ở bảng dưới đây:
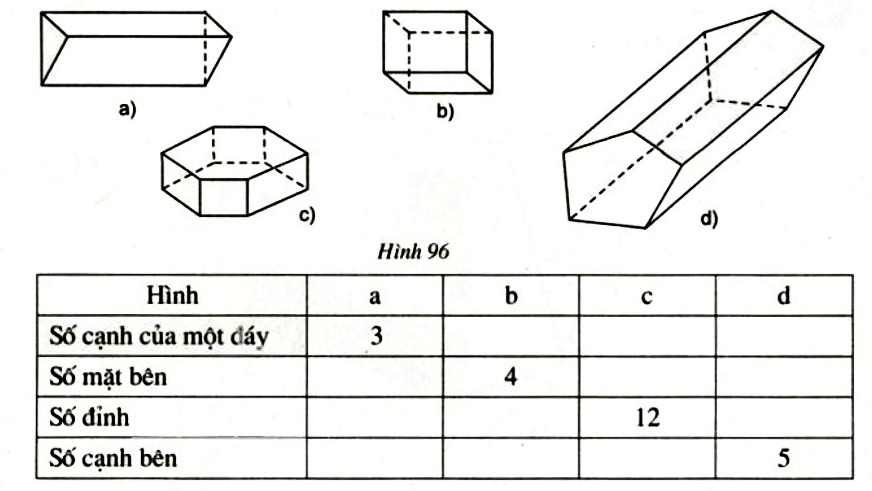
Lời giải:
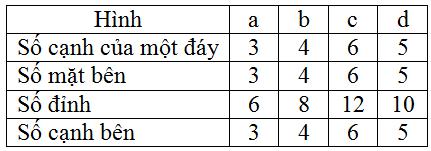
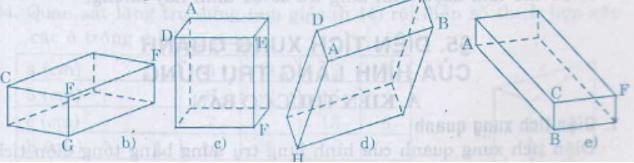
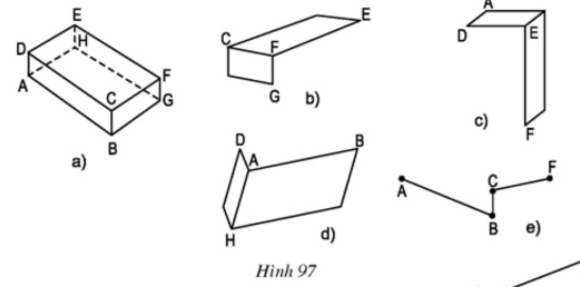
Bài 6 Vẽ lại các hình sau vào vở rồi vẽ thêm các cạnh vào các hình 97b, c, d, e để có một hình hộp hoàn chỉnh (như hình 97a).
Hình 97
Lời giải:
Bài 7 ABC.A’B’C’ là một lăng trụ đứng tam giác (h.98).
a) Những cặp mặt nào song song với nhau?
b) Những cặp mặt nào vuông góc với nhau?
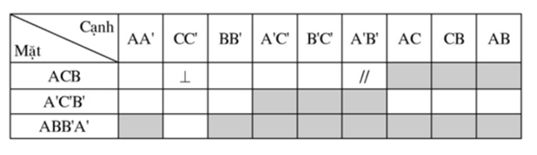
c) Sử dụng kí hiệu “//” và “⊥” để điền vào các ô trống ở bảng sau:
Lời giải:
a) Những cặp mặt phẳng song song nhau: (ABC) // (A’B’C’)
b) Những cặp mặt phẳng vuông góc với nhau: (ABB’A’) ⊥ (A’B’C); (ACC’A’) ⊥ (A’B’C’); (BCC’B’) ⊥ (A’B’C); (ABB’A’) ⊥ (ABC); (ACC’A’) ⊥ (ABC); (BCC’B’) ⊥ (ABC)
c) Điền vào ô trống:
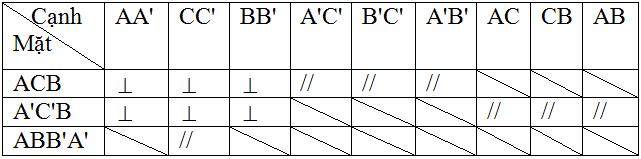
III. Bài tập vận dụng
Bài 1 Vẽ theo hình 99a rồi cắt và gấp lại để được lăng trụ đứng như hình 99b.
Bài 2 Quan sát các lăng trụ đứng trong hình 96 rồi điền số thích hợp vào các ô trống ở bảng dưới đây:
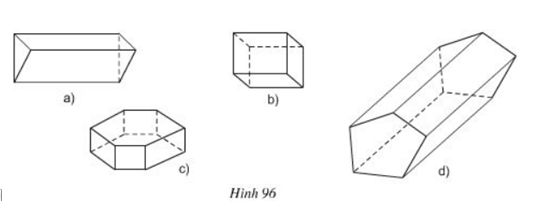
| Hình | a | b | c | d |
| Số cạnh của một đáy | 3 | |||
| Số mặt bên | 4 | |||
| Số đỉnh | 12 | |||
| Số cạnh bên | 5 |
Bài 3 Vẽ lại các hình sau vào vở rồi vẽ thêm các cạnh vào các hình 97b, c, d, e để có một hình hộp hoàn chỉnh (như hình 97a).
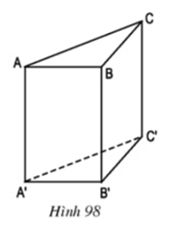
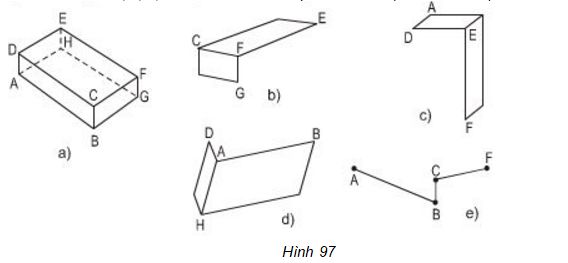
Bài 4 ABC.A’B’C’ là một lăng trụ đứng tam giác (h.98).

a) Những cặp mặt nào song song với nhau?
b) Những cặp mặt nào vuông góc với nhau?
c) Sử dụng kí hiệu “//” và “⊥” để điền vào các ô trống ở bảng sau:
Bài 5 Vẽ theo hình 99a rồi cắt và gấp lại để được lăng trụ đứng như hình 99b.

Bài 6 Hai mặt phẳng chứa hai đáy của một lăng trụ đứng có song song với nhau hay không ?
– Các cạnh bên có vuông góc với hai mặt phẳng đáy hay không ?
– Các mặt bên có vuông góc với hai mặt phẳng đáy hay không ?
Bài 7 Trên hình 94 là tấm lịch để bàn, nó có hình dạng là một lăng trụ đứng. Hãy chỉ rõ các đáy, mặt bên, cạnh bên của lăng trụ.

Bài 8 Quan sát các lăng trụ đứng trong hình 96 rồi điền số thích hợp vào các ô trống ở bảng dưới đây:
Bài 9 Vẽ lại các hình sau vào vở rồi vẽ thêm các cạnh vào các hình 97b, c, d, e để có một hình hộp hoàn chỉnh (như hình 97a).
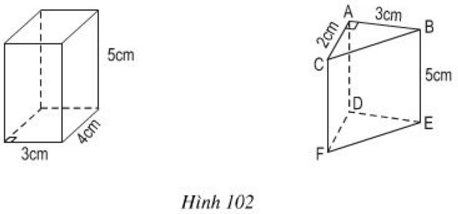
Bài 10 Tính diện tích xung quanh, diện tích toàn phần của các lăng trụ đứng sau đây (h.102):
B. Lý thuyết Diện tích xung quanh của hình lăng trụ đứng
1. Công thức diện tích xung quanh
Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao:
Sxq = 2p.h (p: nửa chu vi đáy, h: chiều cao)
2. Diện tích toàn phần
Diện tích toàn phần của hình lăng trụ đứng bằng tổng diện tích xung quanh và diện tích hai đáy.
Stp = Sxq + 2S (S: điện tích đáy)
Xem thêm