50 Bài tập Diện tích xung quanh của hình chóp đều (có đáp án)- Toán 8

Bài tập Toán 8 Chương 4 Bài 8: Diện tích xung quanh của hình chóp đều

A. Bài tập Diện tích xung quanh của hình chóp đều

I. Bài tập tự luận có giải

Bài 1: Một hình chóp tứ giác đều có thể tích bằng 200cm³, chiều cao bằng 12cm. Tính độ dài cạnh bên.

Lời giải

Xét hình chóp tứ giác đều S.ABCD có V = 200cm³, đường cao SH = 12cm.

Ta có: 

Tức BC² = 50

Tam giác BHC vuông cân nên HB² + HC² = BC² hay 2HC² = BC² hay 2HC² = 50

Suy ra HC² = 25

SC² = SH² + HC² = 12² + 25² = 169 = 13².

Vậy SC = 13cm.

Vậy độ dài cạnh bên là 13cm.

Bài 2 Tính diện tích xung quanh của hình chóp cụt tứ giác đều  có các cạnh đáy bằng 6cm và 8cm, chiều cao của mặt bên bằng 5cm.

Lời giải

Mặt bên hình chóp cụt tứ giác đều là hình thang cân nên diện tích một mặt bên bằng:  

Hình chóp cụt tứ giác đều có 4 mặt bên bằng nhau nên diện tích xung quanh bằng 35.4 = 140 (cm2)

Bài 3: Cắt từ tấm bìa cứng thành các hình như ở hình 118 rồi gấp lại để có những hình chóp đều.

Lời giải

Bài 4 Quan sát hình 120 và điền cụm từ và số thích hợp vào các ô trống ở bảng sau, biết rằng các hình đã cho là những hình chóp đều.

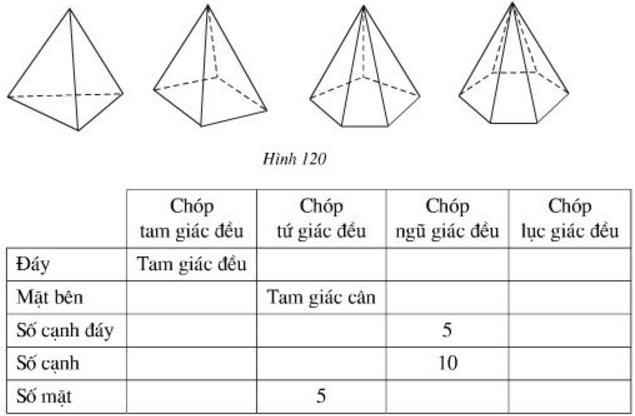
Lời giải:

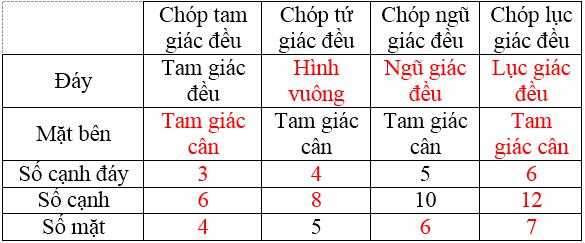
Bài 5 Hãy xét sự đúng sai của các phát biểu sau:

a) Hình chóp đều có đáy là hình thoi và chân đường cao trùng với giao điểm hai đường chéo của đáy.

b) Hình chóp đều có đáy là hình chữ nhật và chân đường cao trùng với giao điểm hai đường chéo của đáy.

Lời giải:

a) Sai, vì hình thoi không phải là tứ giác đều (các góc không bằng nhau).

b) Sai, vì hình chữ nhật không phải là tứ giác đều (các cạnh không bằng nhau).

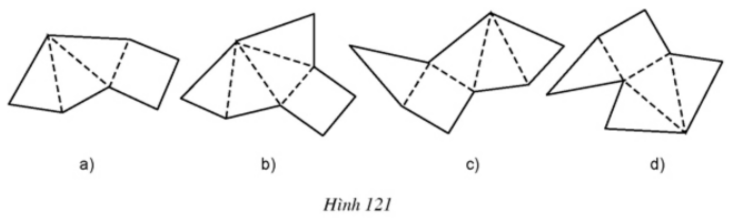
Bài 6 Trong các tấm bìa ở hình 121, em gấp lại tấm bìa nào thì có được một hình chóp đều?

Hình 121

Lời giải:

Hình a khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.

Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.

Hình d khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.

Bài 7 Thực hành: Từ tờ giấy cắt ra một hình vuông rồi thực hiện các thao tác theo thứ tự từ 1 đến 6 để có thể ghép được các mặt bên của một hình chóp tứ giác đều (h.122).

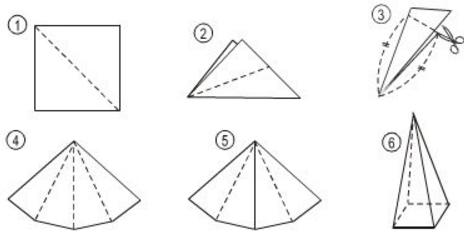
Hình 122

Lời giải:

Các bạn tự thực hành ở nhà để giúp mình dễ tưởng tượng hình chóp đều hơn.

II. Bài tập vận dụng

Bài 1 Quan sát hình 120 và điền cụm từ và số thích hợp vào các ô trống ở bảng sau, biết rằng các hình đã cho là những hình chóp đều.

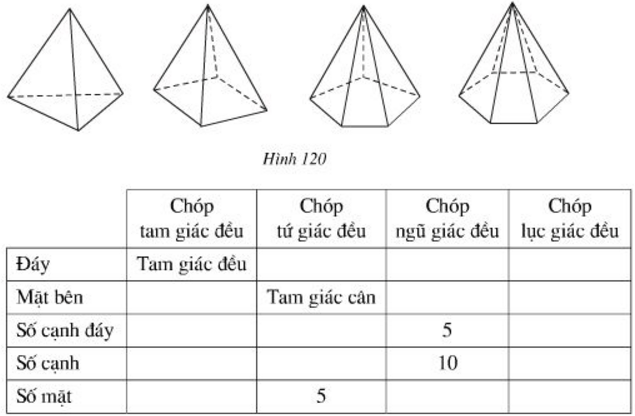
Bài 2 Hãy xét sự đúng sai của các phát biểu sau:

a) Hình chóp đều có đáy là hình thoi và chân đường cao trùng với giao điểm hai đường chéo của đáy.

b) Hình chóp đều có đáy là hình chữ nhật và chân đường cao trùng với giao điểm hai đường chéo của đáy.

Trong các tấm bìa ở hình 121, em gấp lại tấm bìa nào thì có được một hình chóp đều?

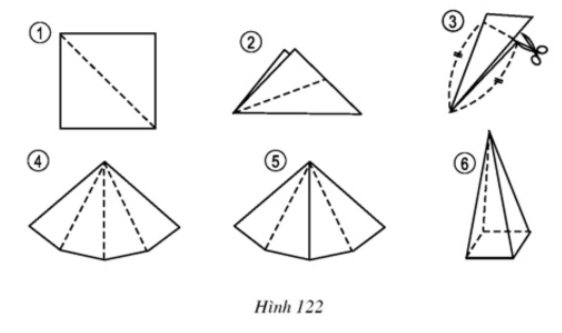
Bài 3 Thực hành: Từ tờ giấy cắt ra một hình vuông rồi thực hiện các thao tác theo thứ tự từ 1 đến 6 để có thể ghép được các mặt bên của một hình chóp tứ giác đều (h.122).

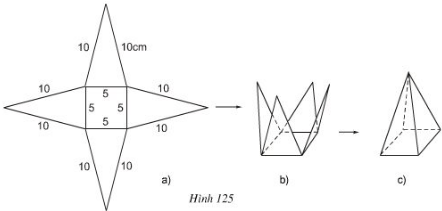
Bài 4 Vẽ, cắt và gấp miếng bìa như hình đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.

a) Trong hình 125a, có bao nhiêu tam giác cân bằng nhau?

b) Sử dụng định lí Pitago để tính chiều cao ứng với đáy của mỗi tam giác.

c) Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu?

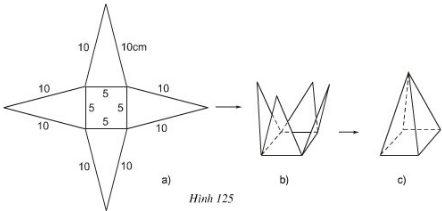
Bài 5 Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước cho trên hình 125.

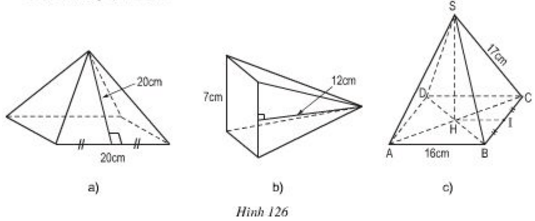
Bài 6 Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây (h.126).

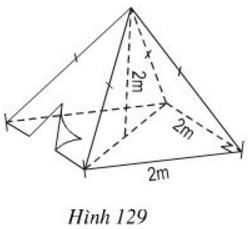
Bài 7 Hình 129 là một cái lều ở trại hè của học sinh kèm theo các kích thước.

a) Thể tích không khí bên trong lều là bao nhiêu?

b) Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp, … biết $\sqrt{5}\approx 2,24$).

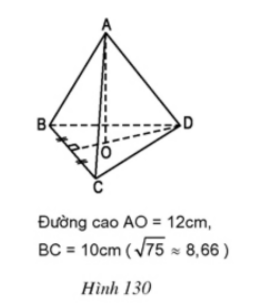
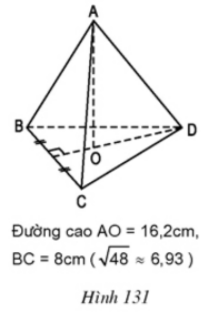
Bài 8 Tính thể tích của mỗi hình chóp đều dưới đây (h.130, h.131).

         

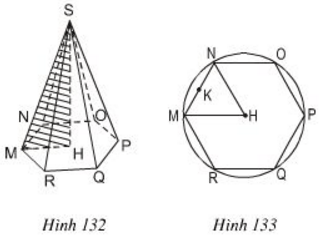
Bài 9 S.MNOPQR là một hình chóp lục giác đều (h.132). Bán kính đường tròn ngoại tiếp đáy (đường tròn tâm H, đi qua sáu đỉnh của đáy) HM = 12cm (h.133), chiều cao SH = 35cm. Hãy tính:

a) Diện tích đáy và thể tích của hình chóp (biết $\sqrt{108}\approx 10,39$);

b) Độ dài cạnh bên SM và diện tích toàn phần của hình chóp (biết $\sqrt{1333}\approx 36,51$).

Bài 10 Tính diện tích toàn phần của:

a) Hình chóp tứ giác đều, biết cạnh đáy a = 5cm, cạnh bên b = 5cm, $\sqrt{1}8,75\approx 4,33$.

b) Hình chóp lục giác đều, biết cạnh đáy a = 6cm, cạnh bên b = 5cm, $\sqrt{3}\approx 1,73$.

B. Lý thuyết Diện tích xung quanh của hình chóp đều

1. Diện tích xung quanh của hình chóp đều

Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn:

S_xq = p.d    (p: nửa chu vi đáy, d: trung đoạn)

2. Diện tích toàn phần của hình chóp

Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích đáy:

S_tp = S_xq + S    (S: diện tích đáy)

Xem thêm