50 Bài tập Chia đa thức một biến đã sắp xếp (có đáp án)- Toán 8

Bài tập Toán 8 Chương 1 Bài 12: Chia đa thức một biến đã sắp xếp

A. Bài tập Chia đa thức một biến đã sắp xếp

I. Bài tập trắc nghiệm

Bài 1: Kết quả của phép chia ( 7x³ – 7x + 42 ):( x² – 2x + 3 ) là ?

A. – 7x + 14

B. 7x + 14

 

C. 7x – 14

D. – 7x – 14

Lời giải:

Ta có phép chia

Chọn đáp án B.

Bài 2: Phép chia x³ + x² – 4x + 7 cho x² – 2x + 5 được đa thức dư là ?

A. 3x – 7.

B. – 3x – 8.

C. – 15x + 7

 

D. – 3x – 7.

Lời giải:

Ta có phép chia

Dựa vào kết quả của phép chia trên, ta có đa thức dư là – 3x – 8.

Chọn đáp án B.

Bài 3: Hệ số a thỏa mãn để 4x² – 6x + a chia hết có x – 3 là ?

A. a = – 18.

B. a = 8.

C. a = 18

D. a = – 8.

Lời giải:

Ta có phép chia

Phép chia trên có số dư là ( a + 18 )

Để 4x² – 6x + a chia hết có x – 3 ⇔ a + 18 = 0 ⇔ a = – 18.

Chọn đáp án A.

Bài 4: Thực hiện phép chia: (4x⁴ + x + 2x³ – 3x²) : (x² + 1) ta được số dư là :

A. – x + 7

B. 4x² + 2x – 7

C. 4x² – 2x + 7

D. x – 7

Lời giải:

Ta có: 4x⁴ + x + 2x³ – 3x² = 4x⁴ + 2x³ – 3x² + x

Vậy: (4x⁴ + x + 2x³ – 3x²) = (4x² + 2x – 7 ).(x² +1) – x + 7

Chọn đáp án A

Bài 5: Thực hiện phép chia (3x³ + 2x + 1 ) : (x + 2) ta được đa thức dư là :

A. 10

B. -9

C. – 15

D. – 27

Lời giải:

Ta có:

Vậy số dư của phép chia đã cho là –27

Chọn đáp án D

Bài 6: Thực hiện phép chia (-4x⁴ + 5x² + x ) : (x² + x) ta được kết quả là:

A. – 4x⁴ + 5x² + x = (x² + x).(-4x² – 4x + 9) – 6x

B. – 4x⁴ + 5x² + x = (x² + x).(4x² + 4x + 9) + 12x

C. – 4x⁴ + 5x² + x = (x² + x).(-4x² + 4x + 9) – 8x

D. – 4x⁴ + 5x² + x = (x² + x). ( 4x² – 4x + 9) + 10x

Lời giải:

Ta có:

Vậy –4x⁴ + 5x² + x = (x² + x).(-4x² + 4x + 9) – 8x

Chọn đáp án C

Bài 7: Cho phép chia: (x³ + 9x² + 27x + 27) : (x + 3). Tìm khẳng định sai?

A. Đây là phép chia hết

B. Thương của phép chia là: (x + 3)²

C. Thương của phép chia là: x² + 6x + 9

D. Số dư của phép chia là: x – 3 .

Lời giải:

Áp dụng hằng đẳng thức đáng nhớ:

(a + b)³ = a³ + 3a²b + 3ab² + b³ ta được:

(x³ + 9x² + 27x + 27) : (x + 3) = (x + 3)³ : (x + 3) = (x + 3)² = x² + 6x +9

Vậy phéo chia đã cho là phép chia hết có thương là: (x + 3)² = x² + 6x + 9.

Chọn đáp án D

Bài 8: Thực hiện phép chia: (x²y + 4xy + 3y ) : (x + 1) ta được thuơng là:

A. xy + 3

B. x + 3y

C. x + y + 3

D. y. (x + 3)

Lời giải:

Ta có: x²y + 4xy + 3y = y.(x² + 4x + 3)

= y.[(x² + x ) + (3x + 3)]

= y.[x.(x + 1) + 3(x + 1)]

= y.(x + 3).(x+1 )

Vậy: (x²y + 4xy + 3y ) : (x + 1) = y.(x + 3).(x + 1) : (x + 1) = y.(x + 3).

Chọn đáp án D

Bài 9: Tìm a để phép chia (x³ – 4x + a): (x – 2) là phép chia hết:

A. a = 0

B. a = 4

C. a = -8

D. a = 8

Lời giải:

Ta có:

Để phép chia đã cho là phép chia hết khi và chỉ khi phần dư bằng 0. Do đó, a =0

Chọn đáp án A

Bài 10: Làm tính chia: (9x³y² + 10x⁴y⁵ – 8x²y²) : x²y²

A. 9x + 10x²y²

B. 9 + 10x²y² – 8

C. 9x + 10x²y³ – 8

D. Đáp án khác

Lời giải:

Ta có: (9x³y² + 10x⁴y⁵ – 8x²y²) : x²y²

= 9x³y² : x²y² + 10x⁴y⁵ : x²y² – 8x²y² : x²y²

= 9x + 10x²y³ – 8

Chọn đáp án C

Bài 11: Kết quả của phép chia (2a³ + 7ab² – 7a² – 2b³) : (2a – b) là

A. (a – b)(a – 2b)

B. (a + b)²   

C. (a – b)(b – 2a)

D. a – b

Lời giải:

Ta có 2a³ + 7ab² – 7a² – 2b³

= 2(a³ – b³) – 7ab(a – b)

= 2(a – b)(a² + ab + b²) – 7ab(a – b)

= (a – b)(2a² – ab – 4ab + 2b²)

= (a – b)[a(2a – b) – 2b(2a – b)]

= (a – b)(2a – b)(a – 2b)

Nên (2a³ + 7ab² – 7a² – 2b3) : (2a – b)

= (a – b)(2a – b)(a – 2b) : (2a – b) = (a – b)(a – 2b)

Đáp án cần chọn là: A

Bài 12: Kết quả của phép chia (x⁴ – x³y + x²y² – xy³) : (x² + y²) là

A. (x – y)    

B. x(x – y)  

C. x² – y     

D. x² + xy

Lời giải:

Ta có x⁴ – x³y + x²y² – xy³

= x⁴ + x²y² – (x³y + xy³)

= x²(x² + y²) – xy(x² + y²)

= (x² + y²)(x² – xy) = (x² + y²)x(x – y)

Nên (x⁴ – x³y + x²y² – xy³) : (x² + y²)

= (x² + y²)x(x – y) : (x² + y²) = x(x – y)

Đáp án cần chọn là: B

Bài 13: Xác định a để đa thức 27x² + a chia hết cho 3x + 2

A. x = 6      

B. a = 12    

C. a = -12   

D. a = 9

Lời giải:

Ta có:

Suy ra 27x² + a + (3x + 2)(9x – 6) + a + 12

Để phép chia trên là phép chia hết thì R = a + 12 = 0 ⇔ a = -12

Đáp án cần chọn là: C

Bài 14: Xác định a để đa thức 10x² – 7x + a chia hết cho 2x – 3

A. a = 24    

B. a = 12    

C. a = -12   

D. a = 9

Lời giải:

(10x² – 7x + a) ⁝ (2x – 3)

Để 10x² – 7x + a chia hết cho 2x – 3 thì a + 12 = 0 ⇔ a = -12

Đáp án cần chọn là: C

Bài 15: Để đa thức x⁴ + ax² + 1 chia hết cho x² + 2x + 1 thì giá trị của a là

A. a = -2     

B. a = 1      

C. a = -1     

D. a = 0

Lời giải:

Phần dư của phép chia đa thức x⁴ + ax² + 1 chia hết cho x² + 2x + 1 là

R = (-4 – 2a)x – a – 2

Để phép chia trên là phép chia hết thì R = 0 ⇔ (-4 – 2a)x – a – 2 = 0 với mọi x

Đáp án cần chọn là: A

II. Bài tập tự luận

Bài 1: Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:

(x³ – 7x + 3 – x²) : (x – 3);

Lời giải:

(x³ – 7x + 3 – x²) : (x – 3)

Sắp xếp lại: (x³ – x² – 7x + 3 ) : (x – 3)

 

Bài 2: Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:

a) (x² + 2xy + y²) : (x + y);

b) (125x³ + 1) : (5x + 1);

Lời giải:

a) (x² + 2xy + y²) : (x + y) = (x + y)² : (x + y) = x + y.

b) (125x³ + 1) : (5x + 1) = [(5x)³ + 1] : (5x + 1)

= (5x)² – 5x + 1 = 25x² – 5x + 1.

Bài 3: Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:

(2x⁴ – 3x² – 3x² – 2 + 6x) : (x² – 2).
Lời giải:

(2x⁴ – 3x² – 3x² – 2 + 6x) : (x² – 2)

Sắp xếp lại: (2x⁴ – 3x² – 3x² + 6x – 2) : (x² – 2)

 

Bài 4: Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:
(x² – 2xy + y²) : (y – x).
Lời giải:

(x² – 2xy + y²) : (y – x) = (x – y)² : [-(x – y)] = – (x – y) = y – x

Hoặc (x² – 2xy + y²) : (y – x) = (y² – 2xy + x²) : (y – x)

= (y – x)² : (y – x) = y – x.

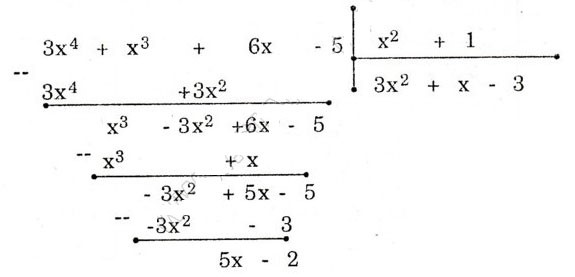
Bài 5: Cho hai đa thức A = 3x⁴ + x³ + 6x – 5 và B = x²+ 1. Tìm dư R trong phép chia A cho B rồi viết A dưới dạng A = B.Q + R.

Lời giải:

Vậy 3x⁴ + x³ + 6x – 5 = (x²+ 1)(3x² + x – 3) + 5x – 2

 

Bài 6: Làm tính chia: (25x⁵ – 5x⁴ + 10x²) : 5x².

Lời giải:

(25x⁵ – 5x⁴ + 10x²) : 5x² = (25x⁵ : 5x² ) – (5x⁴ : 5x² ) + (10x² : 5x²) = 5×3 – x2 + 2

Bài 7: Không thực hiện phép chia, hãy xét xem đa thức A có chia hết cho đa thức B hay không?

A = 15x⁴ – 8x³ + x²

^{B = $\frac{1}{2}$x2}

Lời giải:

Ta có 15x⁴ ; 8x³ ; x² chia hết cho $\frac{1}{2}$x² nên đa thức A chia hết cho B.

Bài 8: Làm tính chia:

(2x⁴ + x³ – 3x² + 5x – 2) : (x² – x + 1).

Lời giải:

Khi đó :(2x⁴ + x³ – 3x² + 5x – 2) = (x² – x + 1)(2x³ + 3x – 2).

 

Bài 9: Tính nhanh:

a) (4x² – 9y²) : (2x – 3y);

b) (27x³ – 1) : (3x – 1);

Lời giải:

a) (4x² – 9y²) : (2x – 3y) = [(2x)² – (3y)²] : (2x – 3y) = (2x –3y)(2x +3y) : (2x –3y) = 2x + 3y;

b) (27x³ – 1) : (3x – 1) = [(3x)³ – 1] : (3x – 1) = (3x – 1) [(3x)² + 3x + 1] : (3x – 1) = 9x²+ 3x + 1

Bài 10: Tìm số a để đa thức 2x³ – 3x² + x + a chia hết cho đa thức x + 2

Lời giải:

 

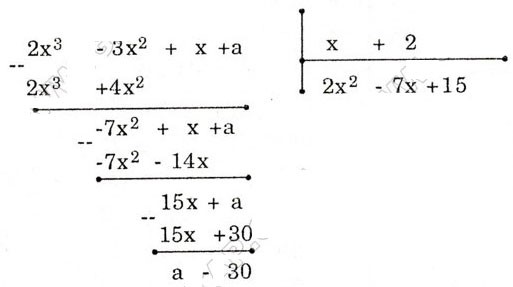
Khi đó 2x³ – 3x² + x + a = (x + 2) (2x² – 7x + 15) + a – 30 để đa thức 2x³ – 3x² + x + a chia hết cho đa thức (x + 2) thì phần dư a – 30 = 0 hay a = 30.

III. Bài tập vận dụng
Bài 1: Tính nhanh:
a, (8x³ + 1) : (4x² – 2x + 1);
b, (x² – 3x + xy -3y) : (x + y)

Bài 2: Không thực hiện phép chia, hãy xét xem đa thức A có chia hết cho đa thức B hay không?

A = x² – 2x + 1

B = 1 – x

Bài 3: Làm tính chia: (15x³y² – 6x²y – 3x²y²) : 6x²y.
Bài 4: Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:

a) (x³ – 7x + 3 – x²) : (x – 3);          

b) (2x⁴ – 3x² – 3x² – 2 + 6x) : (x² – 2).

Bài 5: Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:

a) (x² + 2xy + y²) : (x + y);                      

b) (125x³ + 1) : (5x + 1);

c) (x² – 2xy + y²) : (y – x).

Bài 6: Tìm các số nguyên n thoả mãn giá trị của biểu thức sau:

n³ + 6n² – 7n + 4 sẽ chia hết cho biểu thức n – 2.

Bài 7: Kết quả của phép tính (8x³ − 1) : (1 − 2x) là?

Bài 8: Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:

a. (12x² – 14x + 3 – 6x³ + x⁴) : (1 – 4x + x²)

b. (x⁵ – x² – 3x⁴ + 3x + 5x³ – 5) : (x² – 3x + 5)

Bài 9: Tìm a để đa thức x⁴ – x³ + 6x² – x + a chia hết cho đa thức x² – x + 5.

Bài 10: Tìm giá trị nguyên của n để giá trị biểu thức 3n³ + 10n² – 5 chia hết cho giá trị của biểu thức 3n + 1.

B. Lý thuyết Chia đa thức một biến đã sắp xếp

1. Phép chia hết

 

– Phép chia hết là phép chia có đa thức dư bằng 0.

Quy tắc chia:

+ Sắp xếp các đa thức theo thứ tự giảm dần của biến.

+ Lấy hạng tử cao nhất của đa thức bị chia chia cho hạng tử cao nhất của đa thức chia ta được thương 1.

+ Nhân thương 1 với đa thức chia và lấy đa thức bị chia trừ đi tích đó.

+ Lấy hạng tử cao nhất của đa thức vừa tìm được chia cho hạng tử cao nhất đa thức chia ta được thương 2.

+ Tiếp tục lặp lại các bước trên đến khi nhận được hiệu bằng 0.

Ví dụ 1: Làm tính chia: (x³ – x²  – 5x – 3) : (x – 3).

Lời giải:

Ta có:

 

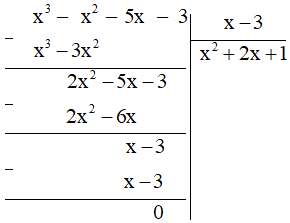
Vậy (x³ – x² – 5x – 3) : (x – 3) = x² + 2x + 1.

2. Phép chia có dư

– Phép chia có dư là phép chia có đa thức dư khác 0.

Quy tắc chia: Làm tương tự phép chia hết đến khi thu được đa thức dư có bậc nhỏ hơn bậc của đa thức chia.

Chú ý: Với hai đa thức tùy ý A và B của cùng một biến (B ≠ 0), tồn tại duy nhất một cặp đa thức Q và R sao cho A = B.Q + R, trong đó R = 0 hoặc bậc của R nhỏ hơn bậc của B (R được gọi là dư trong phép chia A cho B).

Khi R = 0 phép chia A cho B là phép chia hết.

Ví dụ 2: Làm tính chia: (3x³ + 2x² + 5x – 3) : (x² + 1).

Lời giải:

Ta có:

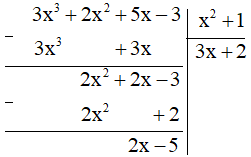
Vậy (3x³ + 2x² + 5x – 3) : (x² + 1) = 3x + 2 (dư 2x – 5)

Hay 3x³ + 2x² + 5x – 3 = (x² + 1).(3x + 2) + 2x – 5.

Xem thêm