Lý thuyết Tam giác cân (Cánh diều 2023) hay, chi tiết | Toán lớp 7

Lý thuyết Toán lớp 7 Bài 7: Tam giác cân

A. Lý thuyết

1. Định nghĩa

Tam giác cân là tam giác có hai cạnh bằng nhau.

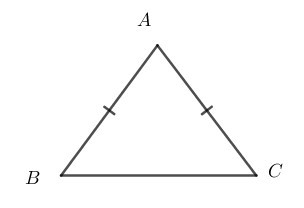
Cho tam giác cân ABC có AB = AC. Khi đó, ta gọi:

• Tam giác ABC là tam giác cân tại A;

• AB, AC là các cạnh bên và BC là cạnh đáy;

• $\widehat{\text{B}}\text{, }\widehat{\text{C}}$ là các góc ở đáy và $\widehat{\text{A}}$ là góc ở đỉnh.

Ví dụ: Tam giác DEF như hình vẽ.

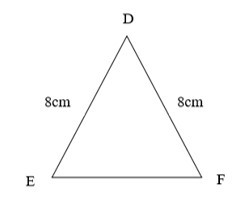
Tam giác DEF là tam giác cân không? Vì sao? Nếu là tam giác cân hãy nêu các cạnh bên, cạnh đáy, các góc ở đáy và góc ở đỉnh của tam giác.

Hướng dẫn giải:

+ Quan sát hình vẽ ta thấy DE = DF = 8 cm

Xét ∆DEF ta có: DE = DF = 8 cm

Nên ∆DEF cân tại D

Vậy ∆DEF là tam giác cân tại D.

+ Tam giác DEF cân tại D có:

• DE, DF là các cạnh bên và EF là cạnh đáy;

• $\widehat{\text{E}}\text{, }\widehat{\text{F}}$ là các góc ở đáy và $\widehat{\text{D}}$là góc ở đỉnh.

2. Tính chất

Trong một tam giác cân, hai góc ở đáy bằng nhau.

Ví dụ:

Cho ∆ABC cân tại A có $\widehat{\text{B}}=\widehat{\text{C}}$ (hình 2)

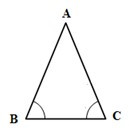
Ví dụ: Cho ∆MNP có MN = MP.

a) Chứng minh $\widehat{\text{N}}=\widehat{\text{P}}.$

b) Giả sử $\widehat{\text{M}}=80°$. Tính số đo góc N và góc P.

Hướng dẫn giải

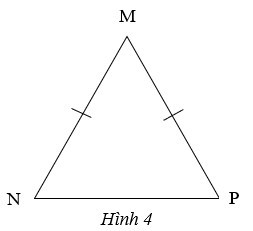
a) Vì ∆MNP có MN = MP nên ∆MNP cân tại M

Do đó $\widehat{\text{N}}=\widehat{\text{P}}$ (tính chất tam giác cân)

Vậy $\widehat{\text{N}}=\widehat{\text{P}}$

b) ∆MNP có $\widehat{\text{M}}+\widehat{\text{N}}+\widehat{\text{P}}=180°$ (định lí tổng ba góc trong một tam giác)

Mà $\widehat{\text{M}}=80°$ nên ta có: $80°+\widehat{\text{N}}+\widehat{\text{P}}=180°$

Hay $\widehat{\text{N}}+\widehat{\text{P}}=180°-80°=100°$  (1)

Theo phần a ta có: $\widehat{\text{N}}=\widehat{\text{P}}$          (2)

Từ (1) và (2) ta có: $\widehat{\text{N}}=\widehat{\text{P}}=\frac{100°}{2}=50°$

Vậy $\widehat{\text{N}}=\widehat{\text{P}}=50°.$

Chú ý:

+ Tam giác vuông có hai cạnh góc vuông bằng nhau được gọi là tam giác vuông cân.

+ Trong tam giác vuông cân, mỗi góc ở đáy bằng 45°.

Ví dụ:

∆ABC vuông cân tại A (hình vẽ bên dưới) có: $\left\{\begin{array}{c}\text{AB = AC}\\ \widehat{\text{B}}=\widehat{\text{C}}=45°\end{array}\right.$

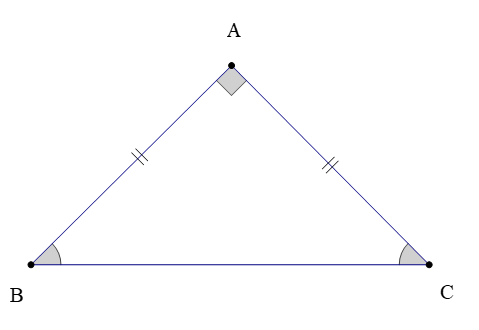
3. Dấu hiệu nhận biết

– Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

– Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

Chú ý:

+ Tam giác có ba cạnh bằng nhau là tam giác đều.

+ Tam giác cân có một góc bằng 60° là tam giác đều.

Ví dụ: Cho tam giác ABC như hình vẽ dưới đây.

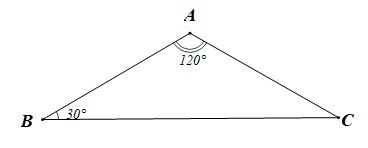
Chứng minh tam giác ABC cân tại A.

Hướng dẫn giải

Xét ∆ABC có: $\widehat{\text{A}}+\widehat{\text{B}}+\widehat{\text{C}}=180°$(định lí tổng ba góc trong một tam giác)

Hay $120°+30°+\widehat{\text{C}}=180°$

Suy ra: $\widehat{\text{C}}=180°-120°-30°=30°$

Xét ∆ABC có $\widehat{\text{B}}=\widehat{\text{C}}=30°$

Do đó ∆ABC cân tại A (dấu hiệu nhận biết)

Vậy ∆ABC cân tại A.

Ví dụ: Cho tam giác DEF có DE = DF.

a) Chứng minh: ∆DEF cân tại D.

b) Giả sử $\widehat{\text{D}}=60°$. Chứng minh: ∆DEF là tam giác đều.

Hướng dẫn giải:

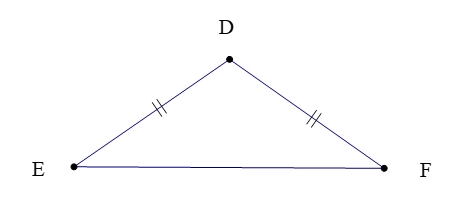
a) Vì ∆DEF có DE = DF nên ∆DEF cân tại D

Vậy ∆DEF cân tại D.

b) Theo phần a ta có: ∆DEF cân tại D

Lại có $\widehat{\text{D}}=60°$

Do đó tam giác DEF là tam giác đều.

4. Vẽ tam giác cân

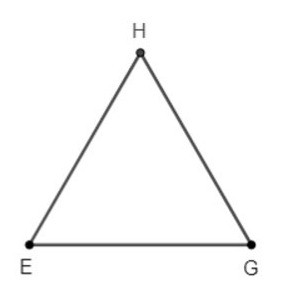
Ví dụ: Dùng thước thẳng (có chia đơn vị) và compa vẽ tam giác HEG cân tại H có cạnh bên HE = HG = a

Để vẽ tam giác HEG, ta làm theo các bước:

– Bước 1: Vẽ đoạn thẳng EG.

– Bước 2: Vẽ cung tròn tâm E bán kính a và cung tròn tâm G bán kính a. Hai cung tròn cắt nhau tại H.

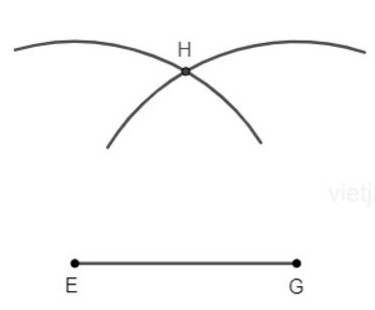
– Bước 3: Vẽ các đoạn HE, HG. Ta nhận được tam giác HEG cân tại H.

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Tìm số đo x trên hình vẽ sau:

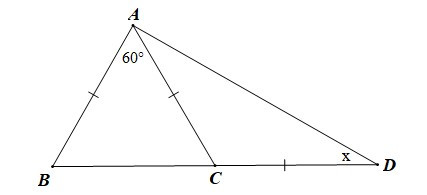
Hướng dẫn giải

Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A.

Lại có $\widehat{\mathrm{BAC}}=60°$ nên ∆ABC đều.

Do đó $\widehat{\mathrm{ACB}}=60°$

Xét ∆CAD có CA = CD nên tam giác CAD cân tại C

Do đó $\widehat{\text{CAD}}=\widehat{\text{D}}=\mathrm{x}$ (tính chất tam giác cân)

Tam giác CAD có: $\widehat{\mathrm{ACB}}=\widehat{\mathrm{CAD}}+\widehat{\mathrm{CDA}}$ (góc ngoài của một tam giác)

Hay 60° = x + x

2x = 60°

x = 60° : 2 = 30°

Vậy x = 30°.

Bài 2. Cho ABC có các tia phân giác trong của góc B và góc C cắt nhau tại I.

Qua I kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại M, N. Chứng minh rằng MN = MB + NC.

Hướng dẫn giải

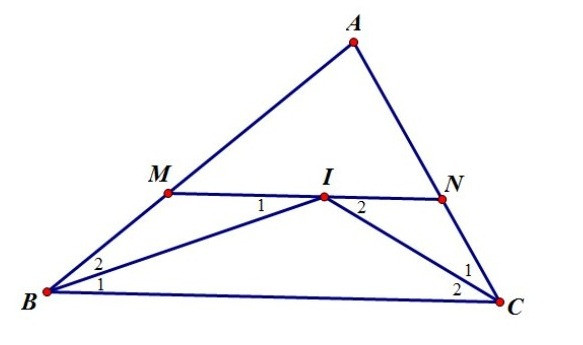
Vì MN//BC nên ${\widehat{\mathrm{I}}}_1={\widehat{\mathrm{B}}}_1$ ( hai góc ở vị trí so le trong) (1)

Và ${\widehat{\mathrm{I}}}_2={\widehat{\mathrm{C}}}_1$ (hai góc ở vị trí so le trong)                (2)

Theo bài ra ta có: BI là tia phân giác của $\widehat{\mathrm{MBC}}$

Do đó ${\widehat{\mathrm{B}}}_1={\widehat{\mathrm{B}}}_2$       (3)

Từ (1) và (3) suy ra ${\widehat{\mathrm{I}}}_1={\widehat{\mathrm{B}}}_2$

Vì ${\widehat{\mathrm{I}}}_1={\widehat{\mathrm{B}}}_2$ nên tam giác MIB cân tại M.

Nên ta có MB = MI.

Do CI là tia phân giác của $\widehat{\mathrm{NCB}}$ nên ${\widehat{\mathrm{C}}}_1={\widehat{\mathrm{C}}}_2$ (4)

Từ (2) và (4) ta có: ${\widehat{\mathrm{I}}}_2={\widehat{\mathrm{C}}}_1$

Vì vậy tam giác NIC cân tại N.

Nên ta có NI = NC

Ta có I nằm giữa M và N nên MN = MI + IN

Hay MN = MB + NC (vì MB = MI; NI = NC).

Vậy MN = MB + NC.

Bài 3. Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác góc A cắt BC tại D. Qua D kẻ đường thẳng vuông góc với BC tại D, cắt AC tại E. Trên AB lấy điểm F sao cho AE = AF. Chứng minh:

a) $\widehat{\text{ABC}}=\widehat{\text{DEC}};$

b) ∆DBF là tam giác cân;

c) DB = DE.

Hướng dẫn giải:

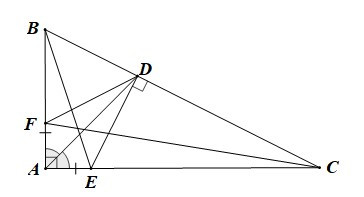
a) Xét ∆ABC vuông tại A có: $\widehat{\text{ABC}}+\widehat{\text{ACB}}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau) (1)

Xét ∆DEC vuông tại D có: $\widehat{\text{DEC}}+\widehat{\text{DCE}}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau)

Hay $\widehat{\text{DEC}}+\widehat{\text{ACB}}=90°$               (2)

Từ (1) và (2) suy ra: $\widehat{\text{ABC}}=\widehat{\text{DEC}}$.

Vậy $\widehat{\text{ABC}}=\widehat{\text{DEC}}$.

b) Xét ∆DFA và ∆DEA có:

AF = AE (giả thiết),

$\widehat{\text{DAF}}=\widehat{\text{DAE}}$ (vì AD là phân giác của $\widehat{\text{BAC}}$),

DA là cạnh chung

Suy ra ∆DFA = ∆DEA (c.g.c)

Suy ra $\widehat{\text{DFA}}=\widehat{\text{DEA}}$ (hai góc tương ứng)     (3)

Ta có $\widehat{\text{DFA}}+\widehat{\text{DFB}}=180°$ (hai góc kề bù)      (4)

Ta lại có: $\widehat{\text{DEA}}+\widehat{\text{DEC}}=180°$ (hai góc kề bù)       (5)

Từ (3); (4) và (5) suy ra $\widehat{\text{DFB}}=\widehat{\text{DEC}}$

Mà theo phần a: $\widehat{\text{ABC}}=\widehat{\text{DEC}}$

Do đó $\widehat{\text{ABC}}=\widehat{\text{DFB}}$ hay $\widehat{\text{FBD}}=\widehat{\text{DFB}}$

Suy ra ∆DBF cân tại D

Vậy ∆DBF cân tại D.

c) Theo phần b ta có: ∆DBF cân tại D

Suy ra DB = DF (tính chất tam giác cân)      (6)

Ta lại có ∆DFA = ∆DEA (chứng minh phần a)

Do đó DF = DE (hai cạnh tương ứng)       (7)

Từ (6) và (7) suy ra: DB = DE.

Vậy DB = DE.

B.2 Bài tập trắc nghiệm

Câu 1. Cho ∆ABC có AB < AC. Ở phía ngoài ∆ABC, vẽ ∆ABD và ∆ACE vuông cân tại A. So sánh AD và AE.

A. AD < AE;                   

B. AD > AE;                   

C. AD = AE;                   

D. Không thể so sánh được.

Hướng dẫn giải

Đáp án đúng là: A

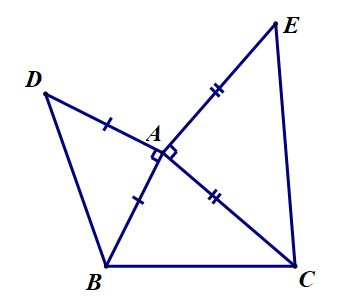
Vì ∆ABD vuông cân tại A nên AB = AD  (1).

Vì ∆ACE vuông cân tại A nên AC = AE  (2).

Lại có AB < AC (giả thiết)  (3).

Từ (1), (2), (3), ta suy ra AD < AE.

Vậy ta chọn đáp án A.

Câu 2. Cho ∆ABC đều. Lấy điểm M, N trên các cạnh AB, AC sao cho AM = AN. ∆AMN là tam giác gì?

A. Tam giác cân tại A;              

B. Tam giác cân tại M;              

C. Tam giác cân tại N;              

D. Tam giác đều.

Hướng dẫn giải

Đáp án đúng là: D

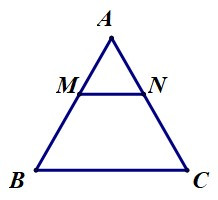
Vì AM = AN (giả thiết).

Nên ∆AMN là tam giác cân tại A.

Mà $\widehat{\mathrm{A}}=60°$ (do ∆ABC đều).

Suy ra ∆AMN là tam giác đều.

Vậy ta chọn đáp án D.

Câu 3. Cho ∆ABC cân tại A, tia phân giác trong của $\widehat{\mathrm{A}}$ cắt BC tại D. Khẳng định nào dưới đây sai?

A. D là trung điểm BC;

B. $\widehat{\mathrm{ABC}}+\widehat{\mathrm{CAD}}=90°$;

C. ∆ADB = ∆ADC;                   

D. $\widehat{\mathrm{ABC}}+\widehat{\mathrm{ADC}}=180°$.

Hướng dẫn giải

Đáp án đúng là: D

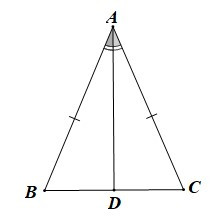
Xét ∆ADB và ∆ADC, có:

AD là cạnh chung,

$\widehat{\mathrm{BAD}}=\widehat{\mathrm{CAD}}$ (do AD là tia phân giác của $\widehat{\mathrm{BAC}}$),

AB = AC (do ∆ABC cân tại A).

Do đó ∆ADB = ∆ADC (c.c.c).

Suy ra đáp án C đúng.

Ta có ∆ADB = ∆ADC (chứng minh trên).

Suy ra BD = CD và $\widehat{\mathrm{ADB}}=\widehat{\mathrm{ADC}}$ (cặp cạnh và cặp góc tương ứng).

Vì BD = CD nên D là trung điểm BC.

Do đó đáp án A đúng.

Ta có $\widehat{\mathrm{ADB}}+\widehat{\mathrm{ADC}}=180°$ (hai góc kề bù).

Suy ra $\widehat{\mathrm{ADB}}=\widehat{\mathrm{ADC}}=180°:2=90°$.

Do đó AD ⊥ BC.

∆ABD vuông tại D: $\widehat{\mathrm{ABD}}+\widehat{\mathrm{BAD}}=90°$.

Mà $\widehat{\mathrm{BAD}}=\widehat{\mathrm{CAD}}$ (AD là phân giác của $\widehat{\mathrm{BAC}}$).

Suy ra $\widehat{\mathrm{ABC}}+\widehat{\mathrm{CAD}}=90°$.

Do đó đáp án B đúng.

Ta có $\widehat{\mathrm{ABC}}+\widehat{\mathrm{CAD}}=90°$.

Suy ra $\widehat{\mathrm{ABC}}<90°$.

Do đó $\widehat{\mathrm{ABC}}+\widehat{\mathrm{ADC}}<90°+90°=180°$.

Do đó đáp án D sai.

Vậy ta chọn đáp án D.

====== ****&**** =====