Cho tam giác ABC vuông tại A. AB = 7,5 cm; BC = 12,5cm.          a) Tính diện tích tam giác ABC.          b) Lấy điểm M trên cạnh AB sao cho AM: MB = 1:2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN.          c) Gọi G, H, I thứ tự là trung điểm của MC, NB và FE. Chứng minh G, H, I thẳng hàng và tính diện tích ∆IHF

Câu hỏi:

Cho tam giác ABC vuông tại A. AB = 7,5 cm; BC = 12,5cm.          a) Tính diện tích tam giác ABC.          b) Lấy điểm M trên cạnh AB sao cho AM: MB = 1:2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN.          c) Gọi G, H, I thứ tự là trung điểm của MC, NB và FE. Chứng minh G, H, I thẳng hàng và tính diện tích ∆IHF

Trả lời:

a) AC = 10cm Þ S_ABC =37,5 (cm²)b) Chứng minh được $\widehat{MAE}=\widehat{AME}$ (cùng = $\widehat{ABC}$) Þ AE = ME. Cmtt ta có AE = NE. Từ đó suy ra ME = NE.c) Chứng minh EH//GF (//MB) và GE//FH (//NC) Þ EGFH là hình bình hành. Chứng minh được $\widehat{HEG}=\widehat{BAC}={90}^0\Rightarrow EGFH$là hình chữ nhật. Suy ra GH đi qua trung điểm của EF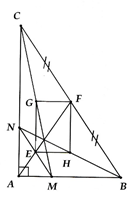.$S_{EGFH}=HE.EG=\frac{1}{2}MB.\frac{1}{2}NC=\frac{1}{4}.\frac{2}{3}AB.\frac{2}{3}AC=\frac{25}{3}\left(c{m}^2\right)$ Mà $S_{EGFH}=4.S\Rightarrow IHF{S}_{IHF}=\frac{25}{12}c{m}^2$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Một đa giác đều có tổng các góc trong bằng 1440°. Số cạnh của đa giác này là:
   
   

   Câu hỏi:
   

   Một đa giác đều có tổng các góc trong bằng 1440°. Số cạnh của đa giác này là:

   Trả lời:

   10

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Diện tích một hình chữ nhật thay đổi như thế nào nếu chiều dài tăng 3 lần, chiều rộng tăng 3 lần
   
   

   Câu hỏi:
   

   Diện tích một hình chữ nhật thay đổi như thế nào nếu chiều dài tăng 3 lần, chiều rộng tăng 3 lần

   Trả lời:

   Diện tích tăng 9 lần

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác MNP vuông tại M, MN = 4 cm, NP = 5 cm. Diện tích tam giác MNP là
   
   

   Câu hỏi:
   

   Cho tam giác MNP vuông tại M, MN = 4 cm, NP = 5 cm. Diện tích tam giác MNP là

   Trả lời:

   6 cm²

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC đường trung tuyến AM . Kết quả nào sau đây là sai
   
   

   Câu hỏi:
   

   Cho tam giác ABC đường trung tuyến AM . Kết quả nào sau đây là sai

   Trả lời:

   S_ABC = S_AMC

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tam giác PMN vuông tại N, E và F thứ tự là trung điểm của MN và MP. Gọi G là điểm đối xứng của F qua E. So sánh SMNp và SMGNF
   
   

   Câu hỏi:
   

   Cho tam giác PMN vuông tại N, E và F thứ tự là trung điểm của MN và MP. Gọi G là điểm đối xứng của F qua E. So sánh S_MNp và S_MGNF

   Trả lời:

   S_MNP =S_MGNF

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====