Cho tam giác ABC có cạnh BC = m. Trên cạnh AB lấy các điểm D, E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự ở M và N. Tính độ dài các đoạn thẳng DM và EN theo m

Câu hỏi:

Cho tam giác ABC có cạnh BC = m. Trên cạnh AB lấy các điểm D, E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự ở M và N. Tính độ dài các đoạn thẳng DM và EN theo m

Trả lời:

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình thang ABCD (AB||CD). Gọi trung điểm của các đường chéo AC và BD là M và N. Chứng minh: MN, AB và CD song song với nhau
   
   

   Câu hỏi:
   

   Cho hình thang ABCD (AB||CD). Gọi trung điểm của các đường chéo AC và BD là M và N. Chứng minh: MN, AB và CD song song với nhau

   Trả lời:

   Gọi P là trung điểm của AD. Ta chứng minh được NP và MP lần lượt là đường trung bình của tam giác ABD và ADC nên suy ra NP//AB và MP//DC. Mặt khác AB//CD nên ta có P, N, M thẳng hàng MN//AB//DC

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho tam giác ABC có điểm M trên cạnh BC sao cho BC = 4cm. Trên cạnh AC lấy điểm N sao cho CNAN = 13 Chứng minh MN song song với AB
   
   

   Câu hỏi:
   

   Cho tam giác ABC có điểm M trên cạnh BC sao cho BC = 4cm. Trên cạnh AC lấy điểm N sao cho $\frac{CN}{AN} = \frac{1}{3}$ Chứng minh MN song song với AB

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hình thang ABCD (AB||CD, AB<CD). Gọi trung điểm của đường chéo BD là M. Qua M kẻ đường thẳng song song với DC cắt AC tại N. Chứng minh:a) N là trung điểm của AC;b) MN=CD−AB2
   
   

   Câu hỏi:
   

   Cho hình thang ABCD (AB||CD, AB<CD). Gọi trung điểm của đường chéo BD là M. Qua M kẻ đường thẳng song song với DC cắt AC tại N. Chứng minh:a) N là trung điểm của AC;b) $MN=\frac{CD-AB}{2}$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC, điểm I nằm trong tam giác, các tia AI, BI, CI cắt các cạnh BC, AC, AB theo thứ tự ở D, E, F. Qua A kẻ đường thẳng song song với BC cắt tia CI tại H và cắt tia BI tại K. Chứng minh:a) AKBD=HADC;b) AFBF+AECE=AIID.
   
   

   Câu hỏi:
   

   Cho tam giác ABC, điểm I nằm trong tam giác, các tia AI, BI, CI cắt các cạnh BC, AC, AB theo thứ tự ở D, E, F. Qua A kẻ đường thẳng song song với BC cắt tia CI tại H và cắt tia BI tại K. Chứng minh:a) $\frac{AK}{BD}=\frac{HA}{DC};$b) $\frac{AF}{BF}+\frac{AE}{CE}=\frac{AI}{ID}.$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
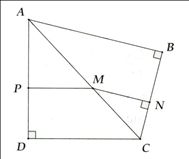
5. Cho tứ giác ABCD có B^=D^=900. Gọi M là điểm bất kì trên đường chéo AC. Gọi N và P lần lượt là hình chiếu của M trên BC và AD. Chứng minh MNAB+MPCD=1.
   
   

   Câu hỏi:
   

   Cho tứ giác ABCD có $\widehat{B}=\widehat{D}={90}^0.$ Gọi M là điểm bất kì trên đường chéo AC. Gọi N và P lần lượt là hình chiếu của M trên BC và AD. Chứng minh $\frac{MN}{AB}+\frac{MP}{CD}=1.$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====