Cho một tam giác đều cạnh a. a) Tính độ dài đường cao của tam giác đó theo a.

Câu hỏi:

Cho một tam giác đều cạnh a.
a) Tính độ dài đường cao của tam giác đó theo a.

Trả lời:

Giả sử ABC là tam giác đều cạnh a (hình vẽ).

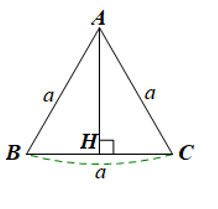
a) Vẽ đường cao AH của tam giác đều ABC.
Khi đó H là trung điểm của BC nên HB = HC = $\frac{1}{2}a$.
Xét tam giác AHC vuông tại H, theo định lí Pythagore ta có:
AC2 = AH2 + HC2
Suy ra AH2 = AC2 – HC2
                   $=a^2-{\left(\frac{1}{2}a\right)}^2=a^2-\frac{1}{4}{a}^2=\frac{3}{4}{a}^2={\left(\frac{\sqrt{3}}{2}\right)}^2.a^2={\left(\frac{a\sqrt{3}}{2}\right)}^2$ 
Do đó $AH=\frac{a\sqrt{3}}{2}$.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

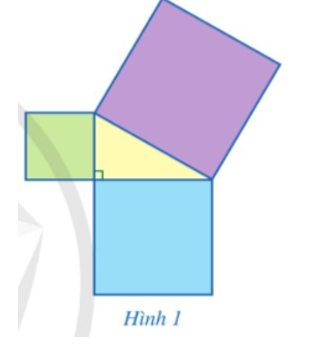
1. Quan sát Hình 1, bạn Đan khẳng định rằng: Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại. Bạn Đan đã dựa vào kiến thức nào để đưa ra khẳng định trên?
   
   

   Câu hỏi:
   

   Quan sát Hình 1, bạn Đan khẳng định rằng: Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại.
   Bạn Đan đã dựa vào kiến thức nào để đưa ra khẳng định trên?
   

   Trả lời:

   Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
   Bạn Đan đã dựa vào Định lí Pythagore để đưa ra khẳng định “Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại”.
   Thật vậy, giả sử A, B, C là ba đỉnh của tam giác (vuông tại A) và độ dài cạnh của các hình vuông lần lượt là a, b, c (hình vẽ).
   

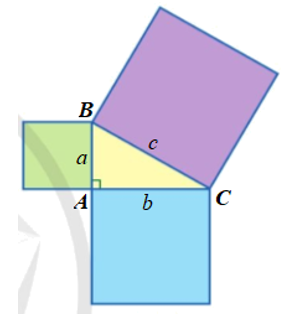
   Diện tích hình vuông nhỏ màu xanh lá cây là: a2 (đơn vị diện tích).
   Diện tích hình vuông nhỏ màu xanh nước biển là: b2 (đơn vị diện tích).
   Diện tích hình vuông lớn màu tím là: c2 (đơn vị diện tích).
   Do tam giác ABC vuông tại A nên theo định lí Pythagore ta có BC2 = AB2 + AC2
   Hay c2 = a2 + b2.
   Vậy diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
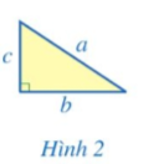
2. Thực hiện các hoạt động sau: a) Vẽ và cắt giấy để có 4 hình tam giác vuông như nhau với độ dài cạnh huyền là a, độ dài hai cạnh góc vuông là b và c, trong đó a, b, c có cùng đơn vị độ dài (Hình 2).
   
   

   Câu hỏi:
   

   Thực hiện các hoạt động sau:
   a) Vẽ và cắt giấy để có 4 hình tam giác vuông như nhau với độ dài cạnh huyền là a, độ dài hai cạnh góc vuông là b và c, trong đó a, b, c có cùng đơn vị độ dài (Hình 2).
   

   Trả lời:

   a) Học sinh thực hiện theo hướng dẫn.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. b) Vẽ hình vuông ABCD có cạnh là b + c như Hình 3. Đặt 4 hình tam giác vuông đã cắt ở câu a lên hình vuông ABCD vừa vẽ, phần chưa bị che đi là hình vuông MNPQ với độ dài cạnh là a (Hình 4).
   
   

   Câu hỏi:
   

   b) Vẽ hình vuông ABCD có cạnh là b + c như Hình 3. Đặt 4 hình tam giác vuông đã cắt ở câu a lên hình vuông ABCD vừa vẽ, phần chưa bị che đi là hình vuông MNPQ với độ dài cạnh là a (Hình 4).
   

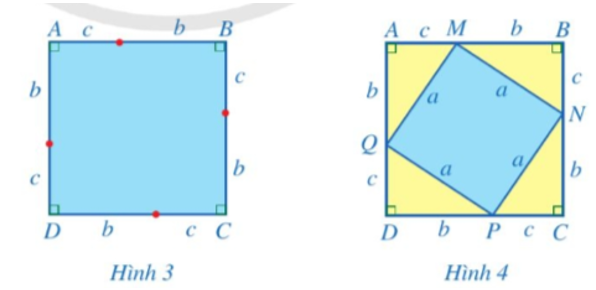
   Trả lời:

   b) Học sinh thực hiện theo hướng dẫn.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. c) Gọi S1 là diện tích của hình vuông ABCD. Gọi S2 là tổng diện tích của hình vuông MNPQ và diện tích của 4 tam giác vuông AQM, BMN, CNP, DPQ. So sánh S1 và S2.
   
   

   Câu hỏi:
   

   c) Gọi S1 là diện tích của hình vuông ABCD. Gọi S2 là tổng diện tích của hình vuông MNPQ và diện tích của 4 tam giác vuông AQM, BMN, CNP, DPQ. So sánh S1 và S2.

   Trả lời:

   c) Diện tích của hình vuông ABCD là: S1 = (b + c)2 (đơn vị diện tích).
   Diện tích của hình vuông MNPQ là: a2 (đơn vị diện tích).
   Diện tích của tam giác vuông AQM là: $\frac{1}{2}bc$ (đơn vị diện tích).
   Tổng diện tích của 4 tam giác vuông AQM, BMN, CNP, DPQ là:
   $4.\frac{1}{2}bc=2bc$ (đơn vị diện tích).
   Khi đó ta có: S2 = a2 + 2bc (đơn vị diện tích).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. d) Dựa vào kết quả ở câu c, dự đoán mối liên hệ giữa a2 và b2 + c2.
   
   

   Câu hỏi:
   

   d) Dựa vào kết quả ở câu c, dự đoán mối liên hệ giữa a² và b² + c².

   Trả lời:

   d) Theo câu b, ta có: diện tích của hình vuông ABCD bằng tổng diện tích của hình vuông MNPQ và diện tích của 4 tam giác vuông AQM, BMN, CNP, DPQ, hay S1 = S2
   Do đó (b + c)2 = a2 + 2bc
   Hay b2 + 2bc + c2 = a2 + 2bc
   Suy ra b2 + c2 = a2.
   Vậy a2 = b2 + c2.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====