Lý thuyết Lôgarit (Kết nối tri thức 2024) hay, chi tiết | Toán lớp 11

Lý thuyết Toán lớp 11 Bài 19: Lôgarit

A. Lý thuyết Lôgarit

1. Khái niệm Lôgarit

Cho a là một số thực dương khác 1 và M là một số thực dương. Số thực $\alpha$ để $a^{\alpha }=M$ được gọi là lôgarit cơ số a của M và kí hiệu là ${\log }_{a}M$.

$\alpha ={\log }_{a}M\iff a^{\alpha }=M$.

Chú ý: Không có lôgarit của số âm và số 0. Cơ số của lôgarit phải dương và khác 1. Từ định nghĩa lôgarit, ta có các tính chất sau:

Với $0<a\ne 1,M>0$ và $\alpha$ là số thực tùy ý, ta có:

$\begin{array}{l}{\log }_{a}1=0;{\log }_{a}a=1;\\ a^{{\log }_{a}M}=M;{\log }_a{a}^{\alpha }=\alpha .\end{array}$

2. Tính chất của lôgarit

a) Quy tắc tính lôgarit

Giả sử a là số thực dương khác 1, M và N là các số thực dương, $\alpha$ là số thực tùy ý. Khi đó:

$\begin{array}{l}{\log }_a\left(MN\right)={\log }_{a}M+{\log }_{a}N;\\ {\log }_a\left(\frac{M}{N}\right)={\log }_{a}M-{\log }_{a}N;\\ {\log }_a{M}^{\alpha }=\alpha {\log }_{a}M.\end{array}$

b) Đổi cơ số của lôgarit

Với các cơ số lôgarit a và b bất kì ($0<a\ne 1,0<b\ne 1$) và M là số thực dương tùy ý, ta luôn có:

${\log }_{a}M=\frac{{\log }_{b}M}{{\log }_{b}a}$.

3. Lôgarit thập phân và lôgarit tự nhiên

a) Lôgarit thập phân

Lôgarit cơ số 10 của một số dương M gọi là lôgatit thập phân của M, kí hiệu là $\log M$ hoặc $\lg M$ (đọc là lốc của M).

b) Số e và lôgarit tự nhiên

Lôgarit cơ số e của một số dương M gọi là lôgarit tự nhiên của M, kí hiệu là $\ln M$ (đọc là lôgarit Nêpe của M).

Sơ đồ tu duy Lôgarit

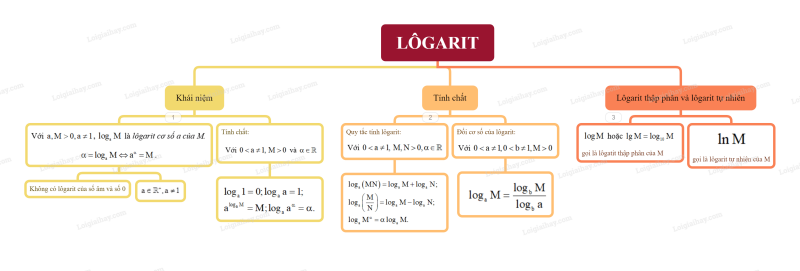
B. Bài tập Lôgarit

Đang cập nhật …

Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 18: Lũy thừa với số mũ thực

Lý thuyết Bài 19: Lôgarit

Lý thuyết Bài 20: Hàm số mũ và hàm số lôgarit

Lý thuyết Bài 21: Phương trình, bất phương trình mũ và lôgarit

Lý thuyết Bài 22: Hai đường thẳng vuông góc