50 Bài tập Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử (có đáp án)- Toán 8

Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 1 Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử. Mời các bạn đón xem:

A. Bài tập Phân tích đa thức thành nhân tử

I. Bài tập trắc nghiệm

Câu 1: Phân tích đa thức ${x^2} + 2xy - 16{a^2} + {y^2}$ thành nhân tử ta được

A. $\left( {x + 4a - y} \right)\left( {x + 4a + y} \right)$	B. $4a\left( {x + y} \right)\left( {x - y} \right)$
C. $\left( {x + y} \right)\left( {x - y} \right)\left( {x - 4a} \right)$	D. $\left( {x + y - 4a} \right)\left( {x + y + 4a} \right)$

Câu 2: Phân tích đa thức ${x^2} - 25 + {y^2} - 2xy$ thành nhân tử ta được:

A. $\left( {x - y + 5} \right)\left( {x - y - 5} \right)$	B. $5\left( {x - y} \right)\left( {x + y} \right)$
C. $\left( {x + y - 5} \right)\left( {x + y + 5} \right)$	D. $\left( {5x + 5y} \right)\left( {x - y} \right)$

Câu 3: Phân tích đa thức ${x^2} + 3x - xy - 3y$ thành nhân tử ta được:

A. $\left( {x - y} \right)\left( {x - 3} \right)$	B. $\left( {x + y} \right)\left( {x + 3} \right)$
C. $\left( {x + y} \right)\left( {x - 3} \right)$	D. $\left( {x - y} \right)\left( {x + 3} \right)$

Câu 4: Giá trị của $3{a^2} - 4b + 4a - 3{b^2}$ tại $a = {2^{2020}};b = {4^{1010}}$ bằng:

A. 0

B. 1

C. 2

D. 3

Câu 5: Giá trị x thỏa mãn ${x^3} + {x^2} - x - 1 = 0$ là:

A. $x = 1$

B. $x = - 1$

C. $x = 0$

D. $x = 2$

II. Bài tập tự luận

Bài 1: Phân tích các đa thức sau thành nhân tử:

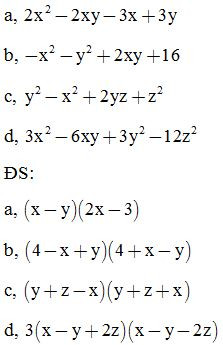
Các phương pháp phân tích đa thức thành nhân tử chi tiết nhất – Toán lớp 8 (ảnh 1)

Bài 2: Phân tích các đa thức sau thành nhân tử:

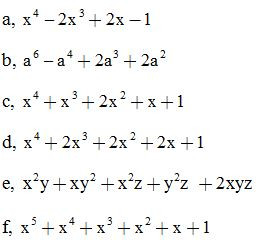
Các phương pháp phân tích đa thức thành nhân tử chi tiết nhất – Toán lớp 8 (ảnh 1)

ĐS:

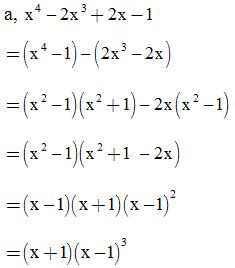
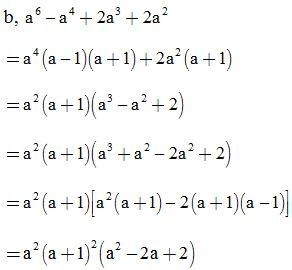
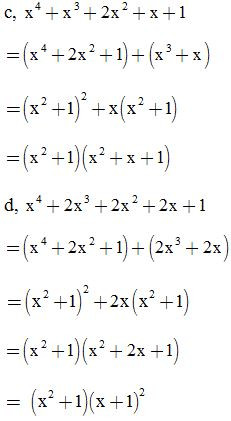
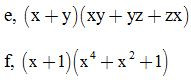
Các phương pháp phân tích đa thức thành nhân tử chi tiết nhất – Toán lớp 8 (ảnh 1)

Bài 3: Phân tích đa thức thành nhân tử rồi tính giá trị của biểu thức:

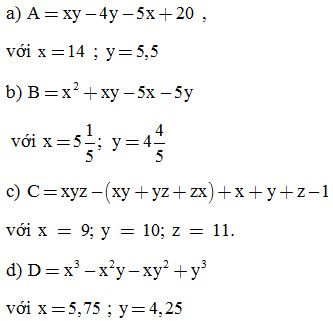
Các phương pháp phân tích đa thức thành nhân tử chi tiết nhất – Toán lớp 8 (ảnh 1)

ĐS:

a, A = 5

b, B = 2

c, C = 720

d, D = 22,5

Bài 4: Tính nhanh

a, 9³ – 9² .(-1) – 9.11 + (-1).11

b, 2016.2017 – 2017²

ĐS:

a, 700

b, – 1

Bài 5: Tìm x biết

a, $3 x^{4} - 9 x^{3}$ $= - 9 x^{2} + 27 x$

b, $x^{2} (x + 8) + x^{2} = - 8 x$

ĐS:

a, x = 0, x = 3

b, x = -8, x = -1, x = 0

Bài 6: Phân tích các đa thức sau thành nhân tử.

a) a⁴ – 8a³ + a² – 8a;

b) x² – bx + ax – ab;

c) 2xy + 4z + 8y + xz.

Lời giải:

a) a⁴ – 8a³ + a² – 8a

= a³(a – 8) + a(a – 8)

= (a³ + a)(a – 8)

= a(a² + 1)(a – 8)

b) x² – bx + ax – ab

= x(x – b) + a(x – b)

= (x – b)(x + a)

c) 2xy + 4z + 8y + xz

= (2xy + xz) + (4z + 8y)

= x(2y + z) + 4(z + 2y)

= (z + 2y)(x + 4).

Bài 7: Tìm x biết:

x(x + 2) + x² = – 2x.

Lời giải:

x(x + 2) + x² = – 2x

x(x + 2) + x² + 2x = 0

x(x + 2) + x(x + 2) = 0

2x(x + 2) = 0

$\Rightarrow [\begin{array}{l} 2 x = 0 \\ x + 2 = 0 \end{array}$ $\Rightarrow [\begin{array}{l} x = 0 \\ x = - 2 \end{array}$

Vậy x = 0; x = – 2 .

Bài 8: Tính nhanh:

a) 15.55 + 37.122 + 15.45 – 37.22;

b) 25² + 35² – 90 + 70.25.

Lời giải:

a) 15.55 + 37.122 + 15.45 – 37.22

= (15.55 + 15.45) + (37.122 – 37.22)

= 15.(55 + 45) + 37. (122 – 22)

= 15.100 + 37. 100

= (15 + 37).100

= 52 . 100

= 5200

b) 25² + 35² – 90 + 70.25

= 25² + 70.25 + 35² – 90

= 25² + 2.25.35 + 35² – 90

= (25 + 35)² – 90

= 60²– 90

= 3600 – 90

= 3510.

Bài 9: Tính giá trị của biểu thức A = x² + y² – 9z² + 2xy khi x + y – 3z = 0.

Lời giải:

A = x² + y² – 9z² + 2xy

A = x² + 2xy + y² – 9z²

A = (x + y)² – (3z)²

A = (x + y – 3z)(x + y + 3z)

Thay x + y – 3z = 0 vào A, ta được: A = 0.(x + y + 3z) = 0.

III. Bài tập vận dụng

Bài 1: Phân tích các đa thức sau thành nhân tử

a, $2{x^2} + 7x + 3$	b, ${x^2} - 2x - 8$
c, $3{x^2} - 11x + 6$	d, ${a^2} - ac - bc + 2ab + {b^2}$
e, $4{x^2} - {y^2} + 4x + 1$	f, $2{x^2} - 2xy - 7x + 7y$

Bài 2: Tìm x, biết:

a, $5x\left( {x - 3} \right) - 2x + 6 = 0$

b, $9\left( {3x - 2} \right) = x\left( {2 - 3x} \right)$

B. Lý thuyết Phân tích đa thức thành nhân tử

Khái niệm: Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

– Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử là cách nhóm các hạng tử phù hợp nhằm xuất hiện nhân tử chung hoặc sẻ dụng các hằng đẳng thức.

– Ta vận dụng phương pháp nhóm hạng tử khi không thể phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung hay bằng phương pháp dùng hằng đẳng thức.

Ví dụ: Phân tích đa thức x² – 4x + xy – 4y thành nhân tử.

Lời giải:

x² – 4x + xy – 4y

= (x² – 4x) + (xy – 4y)

= x(x – 4) + y(x – 4)

= (x – 4)(x + y)

Xem thêm

A. Bài tập Phân tích đa thức thành nhân tử

Bài liên quan:

Leave a Comment Hủy