Lý thuyết Ôn tập chương 7 (Cánh diều 2023) hay, chi tiết | Toán lớp 7

Lý thuyết Toán lớp 7 Ôn tập chương 7

A. Lý thuyết

1. Tổng ba góc của một tam giác

– Định lí: Tổng ba góc của một tam giác bằng 180°.

– Chú ý:

+ Tam giác có ba góc cùng nhọn gọi là tam giác nhọn.

+ Tam giác có một góc vuông gọi là tam giác vuông.

+ Tam giác có một góc tù gọi là tam giác tù.

– Nhận xét: Trong một tam giác vuông, tổng hai góc nhọn bằng 90°.

– Góc ngoài của tam giác:

+ Góc ngoài của một tam giác là góc kề bù với một góc trong của một tam giác đó.

+ Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

2. Quan hệ giữa góc và cạnh đối diện trong một tam giác

2.1. Góc đối diện với cạnh lớn hơn

– Trong tam giác ABC:

• Góc A được gọi là góc đối diện với cạnh BC;

• Góc B được gọi là góc đối diện với cạnh CA;

• Góc C được gọi là góc đối diện với cạnh AB.

– Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

Trong tam giác ABC, nếu AC > AB thì $\widehat{\mathrm{B}}>\widehat{\mathrm{C}}.$

2.2. Cạnh đối diện với góc lớn hơn

– Trong tam giác ABC:

• Cạnh BC được gọi là cạnh đối diện với góc A;

• Cạnh CA được gọi là cạnh đối diện với góc B;

• Cạnh AB được gọi là cạnh đối diện với góc C.

– Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Trong tam giác ABC, nếu $\widehat{\mathrm{B}}>\widehat{\mathrm{C}}$ thì AC > AB.

– Nhận xét:

+ Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.

+ Trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

3. Bất đẳng thức tam giác

– Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

Trong tam giác ABC, ta có: AB + BC > AC; AB + AC > BC; AC + BC > AB.

Các bất đảng thức này gọi là các bất đẳng thức tam giác.

– Nhận xét: Trong một tam giác, hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại.

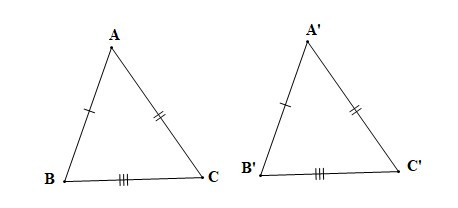
4. Hai tam giác bằng nhau

– Định nghĩa: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

– Khi tam giác ABC và tam giác A’B’C’ bằng nhau thì ta kí hiệu là: DABC = DA’B’C’.

– Quy ước: Khi viết hai tam giác bằng nhau, tên đỉnh của hai tam giác đó phải viết theo đúng thứ tự tương ứng với sự bằng nhau.

– Chú ý:

+ Nếu AB = A’B’, AC = A’C’, BC = B’C’ và $\widehat{\mathrm{A}}=\widehat{{\mathrm{A}}^{‘}},\widehat{\mathrm{B}}=\widehat{{\mathrm{B}}^{‘}},\widehat{\mathrm{C}}=\widehat{{\mathrm{C}}^{‘}}$ thì DABC = DA’B’C’.

+ Nếu DABC = DA’B’C’ thì AB = A’B’, AC = A’C’, BC = B’C’ và $\widehat{\mathrm{A}}=\widehat{{\mathrm{A}}^{‘}},$$\widehat{\mathrm{B}}=\widehat{{\mathrm{B}}^{‘}},$ $\widehat{\mathrm{C}}=\widehat{{\mathrm{C}}^{‘}}.$

Ở đây:

• Hai góc A và A’ (B và B’, C và C’) là hai góc tương ứng;

• Hai cạnh AB và A’B’ (BC và B’C’, AC và A’C’) là hai cạnh tương ứng.

5. Trường hợp bằng nhau cạnh – cạnh – cạnh (c.c.c)

– Tính chất: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

 Nếu AB = A’B’, AC = A’C’, BC = B’C’ thì DABC = DA’B’C’ (c.c.c).

Ví dụ: Cho $\widehat{\mathrm{xOy}},$ trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Vẽ các cung tròn tâm A và B có cùng bán kính sao cho chúng cắt nhau ở điểm I nằm trong góc xOy. Chứng minh OI là tia phân giác của góc xOy.

Hướng dẫn giải

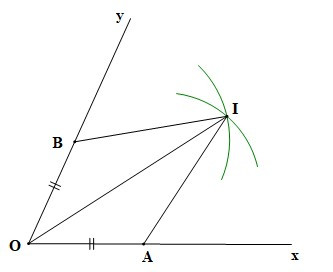
Vì các cung tròn tâm A và tâm B có cùng bán kính cắt nhau ở điểm I nằm trong góc xOy (giả thiết) nên ta có AI = BI

Xét tam giác OAI và tam giác OBI có:

OA = OB (giả thiết),

AI = BI (chứng minh trên),

OI là cạnh chung.

Suy ra DOAI = DOBI (c.c.c).

Do đó $\widehat{\mathrm{AOI}}=\widehat{\mathrm{BOI}}$ (hai góc tương ứng)

Nên tia OI là tia phân giác của góc xOy.

Vậy tia OI là tia phân giác của góc xOy.

– Nhận xét: Cách vẽ tia phân giác của một góc đã được chứng minh cụ thể như trên.

6. Áp dụng vào trường hợp bằng nhau về cạnh huyền và cạnh góc vuông của tam giác vuông

– Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Hai tam giác ABC và A’B’C’ có $\widehat{\mathrm{A}}=\widehat{{\mathrm{A}}^{‘}}=90°,$ BC = B’C’, AB = A’B’ thì DABC = DA’B’C’ (cạnh huyền – cạnh góc vuông).

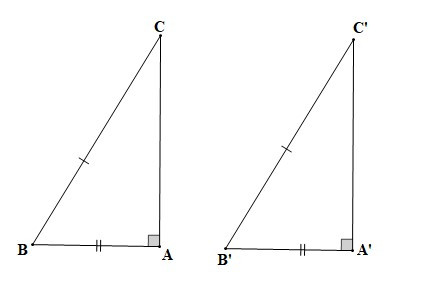
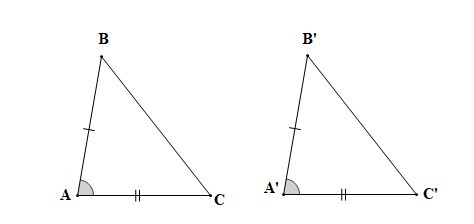
7. Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c)

– Tính chất: Nếu hai cạnh và góc xen giữa của tam giác này lần lượt bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Nếu AB = A’B’, $\widehat{\mathrm{A}}=\widehat{\mathrm{A}‘}$, AC = A’C’ thì DABC = DA’B’C’ (c.g.c).

8. Áp dụng vào trường hợp bằng nhau về hai cạnh góc vuông của tam giác vuông

– Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Nếu $\widehat{\mathrm{A}}=\widehat{\mathrm{A}‘}=90°,$AB = A’B’, AC = A’C’ thì DABC = DA’B’C’.

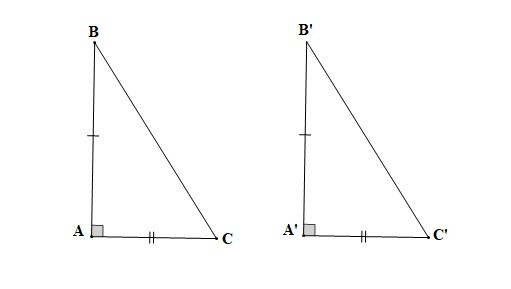
9. Trường hợp bằng nhau góc – cạnh – góc

– Tính chất: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Nếu $\widehat{\mathrm{A}}=\widehat{{\mathrm{A}}^{‘}}$, AB = A’B’, $\widehat{\mathrm{B}}=\widehat{{\mathrm{B}}^{‘}}$ thì DABC = DA’B’C’ (g.c.g).

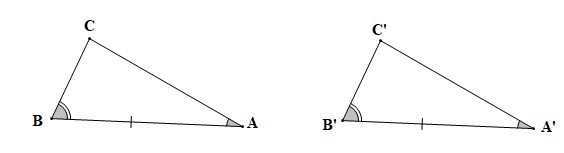
10. Áp dụng vào trường hợp bằng nhau về cạnh góc vuông (hoặc cạnh huyền) và góc nhọn của tam giác vuông

10.1. Trường hợp bằng nhau về cạnh góc vuông và góc nhọn của tam giác vuông

– Nếu một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Nếu $\widehat{\mathrm{A}}=\widehat{\mathrm{A}‘}=90°$, AB = A’B’, $\widehat{\mathrm{B}}=\widehat{\mathrm{B}‘}$ thì DABC = DA’B’C’ (cạnh góc vuông – góc nhọn kề).

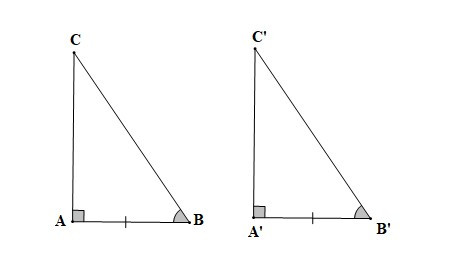
10.2. Trường hợp bằng nhau về cạnh huyền và góc nhọn của tam giác vuông

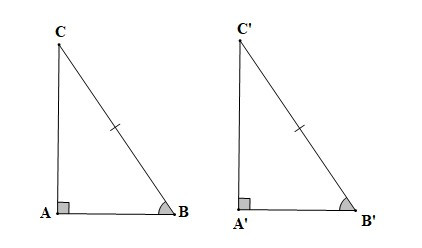
– Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Nếu $\widehat{\mathrm{A}}=\widehat{\mathrm{A}‘}=90°$, BC = B’C’, $\widehat{\mathrm{B}}=\widehat{\mathrm{B}‘}$ thì DABC = DA’B’C’ (cạnh huyền – góc nhọn).

Ví dụ: Cho góc xOy, Oz là tia phân giác của góc đó. Gọi I là một điểm trên tia Oz (I khác O). Kẻ IM vuông góc với Ox (M ∈ Ox), IN vuông góc với Oy (N ∈ Oy). Biết độ dài đoạn thẳng IM là 2 cm, tính độ dài đoạn thẳng IN?

Hướng dẫn giải

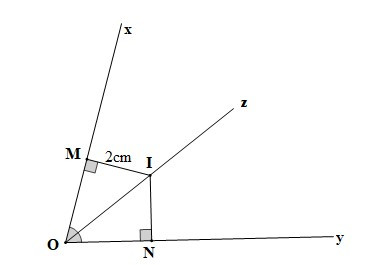
Xét DOIM và DOIN có:

$\widehat{\mathrm{OMI}}=\widehat{\mathrm{ONI}}=90°,$

$\widehat{\mathrm{IOM}}=\widehat{\mathrm{ION}}$ (do Oz là tia phân giác của $\widehat{\mathrm{xOy}}$),

OI là cạnh chung,

Do đó DOMI = DONI (cạnh huyền – góc nhọn)

Suy ra IM = IN (hai cạnh tương ứng)

Mà IM = 2 cm (giả thiết)

Nên IN = 2 cm.

Vậy độ dài đoạn thẳng IN là 2 cm.

– Nhận xét: Độ dài các đoạn thẳng IM, IN gọi là khoảng cách từ điểm I lần lượt đến hai cạnh Ox, Oy của góc xOy. Như vậy ta có thể nói: Nếu một điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.

Ví dụ: Cho góc xOy nhọn. Gọi A là một điểm nằm trong góc xOy. Kẻ AB vuông góc với Ox (B ∈ Ox), AC vuông góc với Oy (C ∈ Oy). Biết AB = AC. Chứng minh rằng điểm A nằm trên tia phân giác của góc xOy.

Hướng dẫn giải

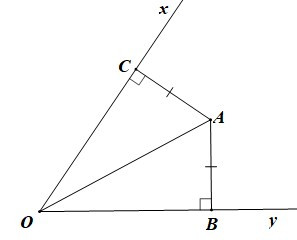
Xét DOAB và DOAC có:

$\widehat{\mathrm{OBA}}=\widehat{\mathrm{OCA}}=90°,$

AB = AC (giả thiết),

OA là cạnh chung.

Do đó DABO = DACO (cạnh huyền – cạnh góc vuông)

Suy ra $\widehat{\mathrm{BOA}}=\widehat{\mathrm{AOC}}$ (hai góc tương ứng).

Do đó OA là tia phân giác của $\widehat{\mathrm{xOy}}.$

Nên A là điểm thuộc tia phân giác của góc xOy.

Vậy điểm A nằm trên tia phân giác của góc xOy.

– Nhận xét: Nếu một điểm nằm trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

11. Vẽ tam giác khi biết ba cạnh

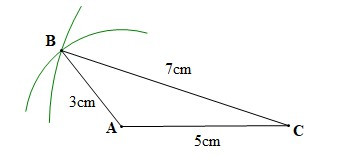
Ví dụ: Để vẽ tam giác ABC có AB = 3 cm, AC = 5 cm, BC = 7 cm bằng thước thẳng (có chia đơn vị) và compa, ta làm như sau:

– Bước 1: Vẽ đoạn thẳng AC = 5 cm

– Bước 2: Vẽ một phần đường tròn tâm A bán kính 3 cm và một phần đương tròn tâm C bán kính 7 cm, B là điểm chung của hai phần đường tròn đó

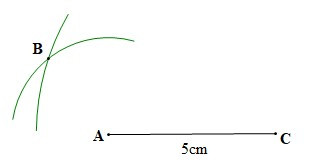
– Bước 3: Vẽ các đoạn thẳng AB, BC. Ta được tam giác ABC.

12. Vẽ tam giác khi biết hai cạnh và góc xen giữa

Để vẽ tam giác ABC có AB = 3 cm, AC = 5 cm, $\widehat{\mathrm{A}}=50°$bằng thước thẳng (có chia đơn vị) và thước đo góc, ta làm như sau:

– Bước 1: Vẽ $\widehat{\mathrm{xAy}}=50°$

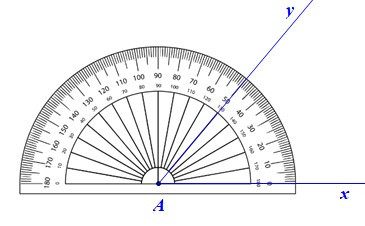
– Bước 2: Trên tia Ax lấy điểm B sao cho AB = 3 cm, trên tia Ay lấy điểm C sao cho AC = 5 cm

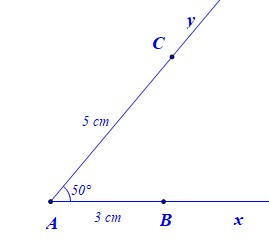
– Bước 3: Vẽ đoạn thẳng BC. Ta được tam giác ABC.

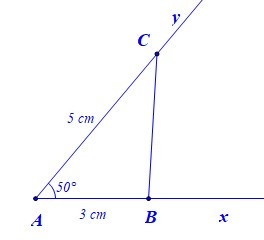
13. Vẽ tam giác khi biết một cạnh và hai góc kề cạnh đó

Ví dụ: Để vẽ tam giác ABC có AB = 5 cm, $\widehat{\mathrm{A}}=60°,\widehat{\mathrm{B}}=70°$ bằng thước thẳng (có chia đơn vị) và thước đo góc, ta làm như sau:

– Bước 1: Vẽ đoạn thẳng AB = 5 cm

– Bước 2: Vẽ các tia Ax, By sao cho $\widehat{\mathrm{BAx}}=60°,\widehat{\mathrm{ABy}}=70°$

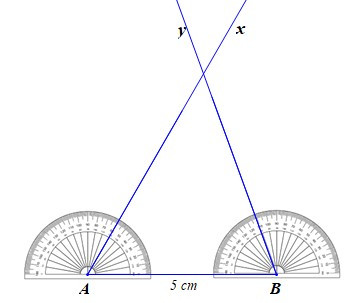
– Bước 3: Vẽ C là điểm chung của hai tia Ax và By. Ta nhận được tam giác ABC.

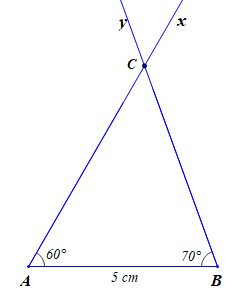
14. Tam giác cân

14.1. Định nghĩa

Tam giác cân là tam giác có hai cạnh bằng nhau.

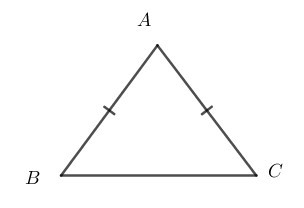
Cho tam giác cân ABC có AB = AC. Khi đó, ta gọi:

• Tam giác ABC là tam giác cân tại A;

• AB, AC là các cạnh bên và BC là cạnh đáy;

• $\widehat{\text{B}}\text{, }\widehat{\text{C}}$ là các góc ở đáy và $\widehat{\text{A}}$ là góc ở đỉnh.

14.2. Tính chất

Trong một tam giác cân, hai góc ở đáy bằng nhau.

Chú ý:

+ Tam giác vuông có hai cạnh góc vuông bằng nhau được gọi là tam giác vuông cân.

+ Trong tam giác vuông cân, mỗi góc ở đáy bằng 45°.

14.3. Dấu hiệu nhận biết

– Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

– Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

Chú ý:

+ Tam giác có ba cạnh bằng nhau là tam giác đều.

+ Tam giác cân có một góc bằng 60° là tam giác đều.

14.4. Vẽ tam giác cân

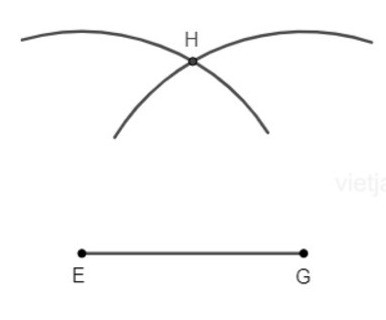
Ví dụ: Dùng thước thẳng (có chia đơn vị) và compa vẽ tam giác HEG cân tại H có cạnh bên HE = HG = a

Để vẽ tam giác HEG, ta làm theo các bước:

– Bước 1: Vẽ đoạn thẳng EG.

– Bước 2: Vẽ cung tròn tâm E bán kính a và cung tròn tâm G bán kính a. Hai cung tròn cắt nhau tại H.

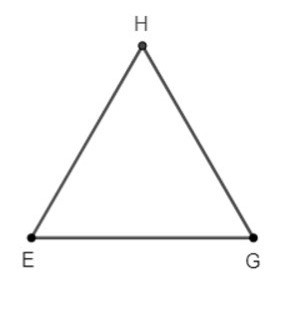
– Bước 3: Vẽ các đoạn HE, HG. Ta nhận được tam giác HEG cân tại H.

15. Đường vuông góc và đường xiên

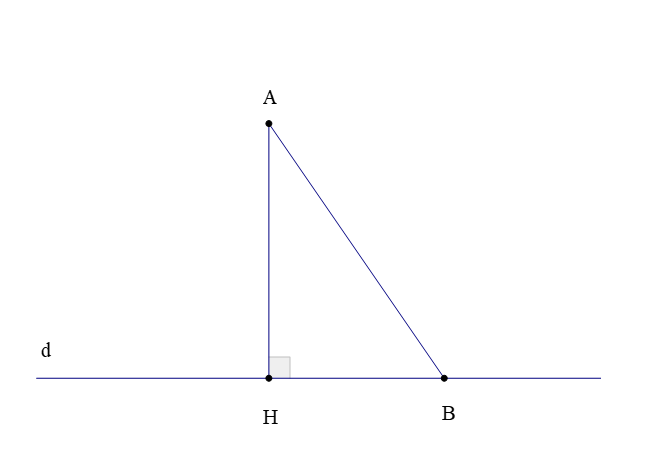
Trong hình vẽ trên, ta gọi:

– Đoạn thẳng AH là đoạn vuông góc hay đường vuông góc kẻ từ điểm A đến đường thẳng d;

– Điểm H là chân của đường vuông góc hay hình chiếu của điểm A trên đường thẳng d;

– Độ dài đoạn thẳng AH là khoảng cách từ điểm A đến đường thẳng d;

– Đoạn thẳng AB là một đường xiên kẻ từ điểm A đến đường thẳng d.

16. Quan hệ giữa đường vuông góc và đường xiên

– Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.

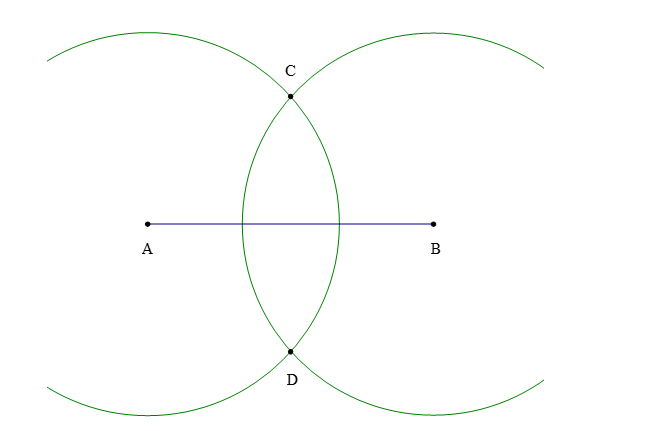
17. Đường trung trực của một đoạn thẳng

17.1. Định nghĩa

– Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng ấy.

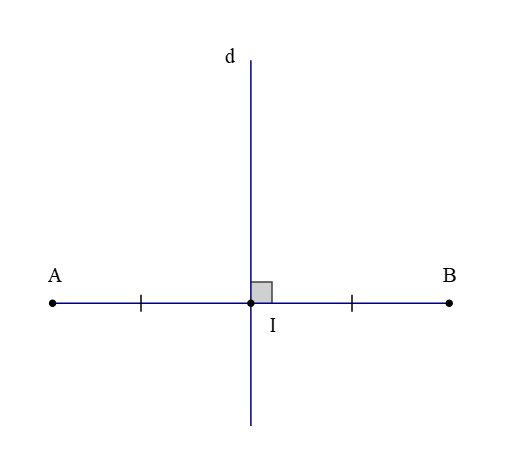
Quan sát hình vẽ trên, ta có:

+ Đoạn thẳng AB; trung điểm I của đoạn thẳng AB;

+ Đường thẳng d ⊥ AB tại I.

Do đó, đường thẳng d là đường trung trực của đoạn thẳng AB.

17.2. Tính chất

– Một điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

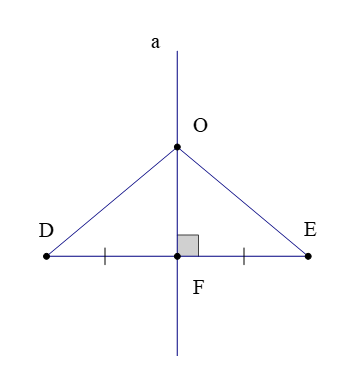
Quan sát hình trên, ta có:

Đường thẳng a là đường trung trực của đoạn thẳng DE;

Điểm O nằm trên đường thẳng a.

Khi đó ta có OD = OE.

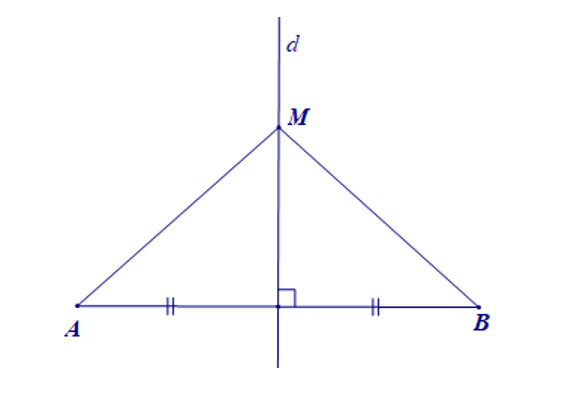
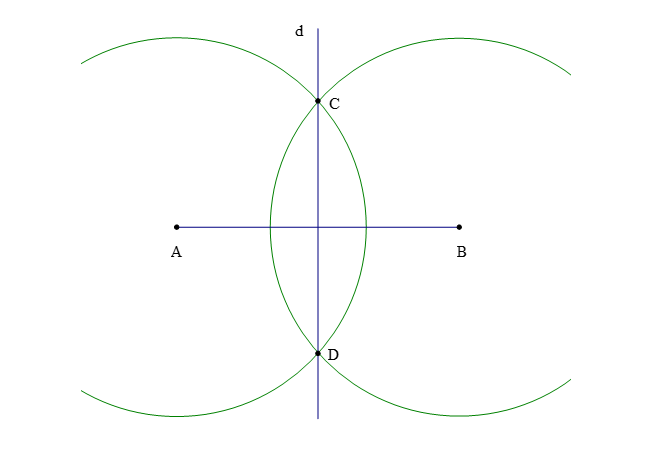
– Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Gọi d là đường trung trực của đoạn thẳng AB, M là điểm sao cho MA = MB (như hình vẽ bên dưới). Ta có M nằm trên đường trung trực d của đoạn thẳng AB.

17.3. Vẽ đường trung trực của một đoạn thẳng

Ví dụ: Dùng thước thẳng (có chia đơn vị) và compa vẽ đường trung trực của đoạn thẳng AB, biết AB = a cm.

Để vẽ đường trung trực của đoạn thẳng AB, ta làm theo các bước:

Bước 1: Vẽ đoạn thẳng AB = a cm.

Bước 2: Vẽ một phần đường tròn tâm A bán kính R (biết R > $\frac{\mathrm{a}}{2}$).

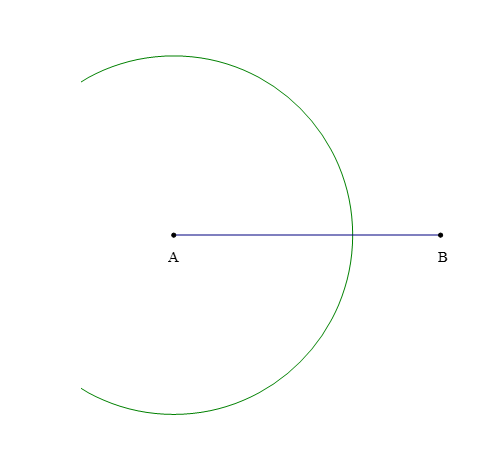
Bước 3: Vẽ một phần đường tròn tâm B bán kính R (biết R > $\frac{\mathrm{a}}{2}$), cắt phần đường tròn tâm A vẽ ở Bước 2 tại các điểm C và D.

Bước 4: Vẽ đường thẳng đi qua hai điểm C và D. Đường thẳng CD là đường trung trực của đoạn thẳng AB.

18. Tính chất ba đường trung tuyến của tam giác

18.1. Đường trung tuyến của tam giác

– Trong tam giác ABC (hình bên dưới), đoạn thẳng AM nối đỉnh A với trung điểm M của cạnh BC được gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc tương ứng với cạnh BC).

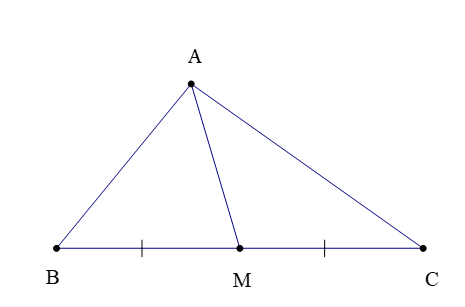
Đôi khi, đường thẳng AM cũng được gọi là đường trung tuyến của ∆ABC.

– Chú ý: Mỗi tam giác có ba đường trung tuyến.

18.2. Tính chất ba đường trung tuyến của tam giác

– Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó được gọi là trọng tâm của tam giác.

Chú ý: Trong tam giác ABC (hình vẽ dưới) có ba đường trung tuyến AM, BK, CN cùng đi qua điểm G, ta còn nói chúng đồng quy tại điểm G.

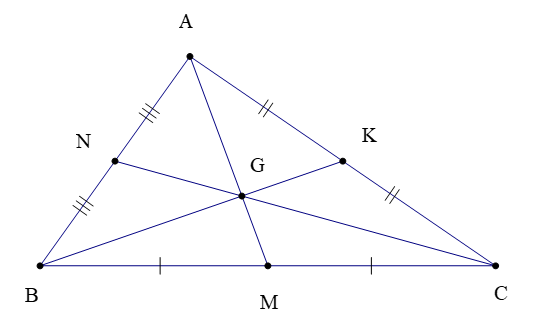
Để xác định trọng tâm của một tam giác, ta chỉ cần vẽ hai đường trung tuyến bất kì và xác định giao điểm của hai đường đó.

Nhận xét: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.

Lưu ý: Trong ∆ABC, với AM là đường trung tuyến và G là trọng tâm ta có:

$\frac{\text{GM}}{\text{AM}}=\frac{1}{3},\frac{\text{GM}}{\text{GA}}=\frac{1}{2}$

19. Tính chất ba đường phân giác của tam giác

19.1. Đường phân giác của tam giác

– Trong tam giác ABC (hình vẽ bên dưới), tia phân giác của $\widehat{\text{A}}$cắt cạnh BC tại D. Khi đó, đoạn thẳng AD được gọi là đường phân giác (xuất phát từ đỉnh A) của tam giác ABC.

Đôi khi, đường thẳng AD cũng được gọi là đường phân giác của ∆ABC.

Nhận xét: Mỗi tam giác có ba đường phân giác.

19.2. Tính chất ba đường phân giác của tam giác

– Ba đường phân giác của một tam giác cùng đi qua một điểm

Nhận xét:

+ Để xác định giao điểm ba đường phân giác của một tam giác, ta chỉ cần vẽ hai đường phân giác bất kì và xác định giao điểm của hai đường đó.

+ Giao điểm ba đường phân giác của một tam giác cách đều ba cạnh của tam giác đó.

– Vậy, trong một tam giác ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác.

20. Tính chất ba đường trung trực của tam giác

20.1. Đường trung trực của tam giác

– Trong một tam giác, đường trung trực của mỗi cạnh được gọi là đường trung trực của tam giác đó.

Chú ý: Đường trung trực của một tam giác có thể không đi qua đỉnh nào của tam giác.

– Nhận xét: Mỗi tam giác có 3 đường trung trực.

20.2. Tính chất ba đường trung trực của tam giác

– Ba đường trung trực của một tam giác cùng đi qua một điểm.

Nhận xét:

+ Để xác định giao điểm ba đường trung trực của một tam giác, ta chỉ cần vẽ hai đường trung trực bất kì và xác định giao điểm của hai đường đó.

+ Giao điểm ba đường trung trực của một tam giác cách đều ba đỉnh của tam giác đó.

Do đó, trong một tam giác ba đường trung trực cùng đi qua một điểm và điểm đó cách đều ba đỉnh của tam giác.

21. Tính chất ba đường cao của tam giác

21.1. Đường cao của tam giác

– Trong một tam giác, đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là một đường cao của tam giác đó.

Trong hình vẽ trên, đoạn thẳng AM là một đường cao của tam giác ABC. Đôi khi, ta cũng gọi đường thẳng AM là một đường cao của tam giác ABC.

Chú ý:

+ Mỗi tam giác có ba đường cao.

+ Đường cao của tam giác có thể nằm trong, trên cạnh hoặc nằm ngoài tam giác.

21.2. Tính chất ba đường cao trong tam giác

– Trong một tam giác, ba đường cao cùng đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác.

Nhận xét: Để xác định trực tâm của một tam giác, ta chỉ cần vẽ hai đường cao bất kì và xác định giao điểm của hai đường đó.

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Cho tam giác ABC vuông tại A có $\widehat{\mathrm{C}}=30°.$ Lấy điểm D nằm trên cạnh AC sao cho $\widehat{\mathrm{CBD}}=20°.$ Tính số đo của:

a) $\widehat{\mathrm{ADB}};$

b) $\widehat{\mathrm{ABD}}.$

Hướng dẫn giải

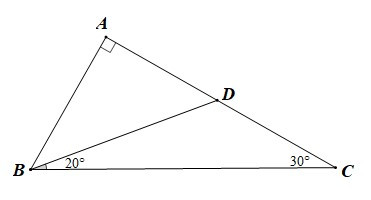
a) Xét DBCD có $\widehat{\mathrm{ADB}}$ là góc ngoài của tam giác tại đỉnh D

Do đó $\widehat{\mathrm{ADB}}=\widehat{\mathrm{C}}+\widehat{\mathrm{CBD}}$ (tính chất góc ngoài của tam giác)

Suy ra $\widehat{\mathrm{ADB}}=30°+20°=50°.$

Vậy $\widehat{\mathrm{ADB}}=50°.$

b) Tam giác ABC vuông tại A nên $\widehat{\mathrm{A}}=90°$

Do đó tam giác ABD vuông tại A.

Khi đó $\widehat{\mathrm{ABD}}+\widehat{\mathrm{ADB}}=90°$ (tổng hai góc nhọn trong tam giác vuông bằng 90°)

Suy ra $\widehat{\mathrm{ABD}}=90°-\widehat{\mathrm{ADB}}$

Do đó $\widehat{\mathrm{ABD}}=90°-50°=40°.$

Vậy $\widehat{\mathrm{ABD}}=40°.$

Bài 2. Cho tam giác MNP có góc M là góc tù. Trên cạnh MN lấy điểm D (D khác M, N), trên MP lấy điểm E (E khác M, P). So sánh DE và NP.

Hướng dẫn giải

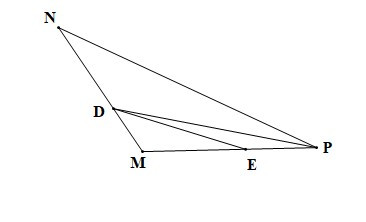
Vì $\widehat{\mathrm{PE}\text{D}}$ là góc ngoài của tam giác DME nên $\widehat{\mathrm{PE}\text{D}}=\widehat{\text{EDM}}+\widehat{\mathrm{M}}$

Mà $\widehat{\mathrm{M}}$ là góc tù (giả thiết) nên $\widehat{\mathrm{PE}\text{D}}$ là góc tù.

Xét tam giác DEP có $\widehat{\mathrm{PE}\text{D}}$ là góc tù, DP là cạnh đối diện với $\widehat{\mathrm{PE}\text{D}}$

Suy ra DE < DP (trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất).

Vì $\widehat{\mathrm{N}\text{D}\mathrm{P}}$ là góc ngoài của tam giác DPM nên $\widehat{\mathrm{N}\text{D}\mathrm{P}}=\widehat{\mathrm{DPM}}+\widehat{\mathrm{M}}$

Mà $\widehat{\mathrm{M}}$ là góc tù (giả thiết) nên $\widehat{\mathrm{N}\text{D}\mathrm{P}}$ là góc tù.

Xét tam giác DNP có $\widehat{\mathrm{N}\text{D}\mathrm{P}}$ là góc tù, NP là cạnh đối diện với $\widehat{\mathrm{N}\text{D}\mathrm{P}}$

Suy ra DP < NP (trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất).

Lại có DE < DP (chứng minh trên).

Suy ra DE < DP < NP.

Vậy DE < NP.

Bài 3. Cho tam giác ABC có $\widehat{\mathrm{B}}=90°,$ AC = 2AB. Gọi D là trung điểm của AC và tia AE là tia phân giác của $\widehat{\mathrm{BAC}}$ (E ∈ BC).

a) Chứng minh ED ⊥ AC;

b) Chứng minh EA = EC;

c) Tính số đo của $\widehat{\mathrm{BAC}},\widehat{\mathrm{BCA}}$ của DABC.

Hướng dẫn giải

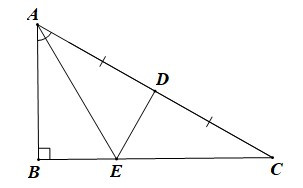
Vì AC = 2AB (giả thiết) nên AB = $\frac{1}{2}$AC.

Vì D là trung điểm AC nên AD = DC = $\frac{1}{2}$AC.

Do đó AB = AD = DC = $\frac{1}{2}$AC.

Xét DABE và DADE có:

AB = AD (chứng minh trên),

$\widehat{\mathrm{BAE}}=\widehat{\mathrm{DAE}}$ (do AE là tia phân giác của $\widehat{\mathrm{BAC}})$

AE là cạnh chung

Do đó DABE = DADE (c.g.c).

Suy ra $\widehat{\mathrm{ABE}}=\widehat{\mathrm{ADE}}$ (hai góc tương ứng)

Mà $\widehat{\mathrm{ABE}}=90°$ (giả thiết)

Do đó $\widehat{\mathrm{ADE}}=90°.$

Hay ED ⊥ AC tại D.

Vậy ED ⊥ AC.

b) Xét DADE và DCDE có:

$\widehat{\mathrm{ADE}}=\widehat{\mathrm{CDE}}=90°$ (do ED ⊥ AC),

AD = DC (chứng minh phần a),

ED là cạnh chung,

Do đó DADE = DCDE (hai cạnh góc vuông)

Suy ra EA = EC (hai cạnh tương ứng).

Vậy EA = EC.

c) Vì DADE = DCDE (chứng minh phần b)

Nên $\widehat{\mathrm{DAE}}=\widehat{\mathrm{DCE}}$ (hai góc tương ứng)

Mà $\widehat{\mathrm{DAE}}=\widehat{\mathrm{BAE}}$ (do AE là tia phân giác của $\widehat{\mathrm{BAC}}$)

Do đó $\widehat{\mathrm{DAE}}=\widehat{\mathrm{DCE}}=\widehat{\mathrm{BAE}}.$

Xét DABC vuông tại B có: $\widehat{\mathrm{BAC}}+\widehat{\mathrm{ACB}}=90°$ (hai góc nhọn trong tam giác vuông bằng 90°).

Suy ra $\widehat{\mathrm{BAE}}+\widehat{\mathrm{DAE}}+\widehat{\mathrm{DCE}}=90°$

Hay $3\widehat{\mathrm{DCE}}=90°$

Do đó $\widehat{\mathrm{DCE}}=30°$ nên $\widehat{\mathrm{BCA}}=30°$

Suy ra $\widehat{\mathrm{DAE}}=\widehat{\mathrm{BAE}}=30°$

Khi đó $\widehat{\mathrm{BAC}}=\widehat{\mathrm{BAE}}+\widehat{\mathrm{DAE}}=30°+30°=60°.$

Vậy DABC có $\widehat{\mathrm{BAC}}=60°$ và $\widehat{\mathrm{BCA}}=30°.$

Bài 4. Cho tam giác ABC cân tại A. Các đường phân giác BE, CF cắt nhau tại H. Chứng minh:

a) AH là trung trực của EF;

b) AH là trung trực của BC.

Hướng dẫn giải

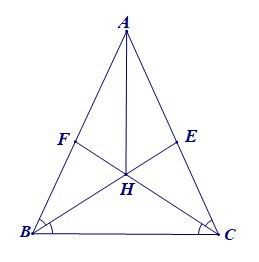
a) Vì BE là phân giác của $\widehat{\text{ABC}}$ nên $\widehat{\text{ABE}}=\widehat{\text{CBE}}=\frac{1}{2}\widehat{\text{ABC}}$  (1)

CF là phân giác của $\widehat{\text{ACB}}$ nên $\widehat{\text{ACF}}=\widehat{\text{FCB}}=\frac{1}{2}\widehat{\text{ACB}}$  (2)

Mà $\widehat{\text{ABC}}=\widehat{\text{ACB}}$ (vì ∆ABC cân tại A)  (3)

Từ (1), (2) và (3) suy ra $\widehat{\text{ABE}}=\widehat{\text{ACF}}$

• Xét ∆ABE và ∆ACF có:

AB = AC (vì ∆ABC cân tại A)

$\widehat{\text{ABE}}=\widehat{\text{ACF}}$ (chứng minh trên)

AH là cạnh chung.

Do đó ∆ABE = ∆ACF (c.g.c)

Suy ra AE = AF (hai cạnh tương ứng)

Suy ra A nằm trên đường trung trực của EF        (4)

• Vì AB = AC và AF = AE (chứng minh trên)

Nên AB – AF = AC – AE

Hay BF = CE.

• Vì ∆ABE = ∆ACF (chứng minh trên)

Nên $\widehat{\mathrm{AEB}}=\widehat{\mathrm{AFC}}$ (hai góc tương ứng)

Mà $\widehat{\mathrm{AEB}}+\widehat{\mathrm{CEB}}=180°$ (hai góc kề bù)

$\widehat{\mathrm{AFC}}+\widehat{\mathrm{BFC}}=180°$(hai góc kề bù)

Do đó $\widehat{\mathrm{CEB}}=\widehat{\mathrm{BFC}}$ hay $\widehat{\mathrm{CEH}}=\widehat{\mathrm{BFH}}$

• Xét ∆BFH và ∆CEH có:

 $\widehat{\mathrm{BFH}}=\widehat{\mathrm{CEH}}$ (chứng minh trên),

BF = CE (chứng minh trên),

$\widehat{\mathrm{FBH}}=\widehat{\mathrm{ECH}}$ (do $\widehat{\text{ABE}}=\widehat{\text{ACF}}$).

Do đó ∆BFH = ∆CEH (g.c.g)

Suy ra HF = HE (hai cạnh tương ứng)

Suy ra H nằm trên đường trung trực của EF          (5)

Từ (4) và (5) suy ra A, H nằm trên đường trung trực của EF

Suy ra AH là đường trung trực của EF

Vậy AH đường trung trực của EF.

b) Vì ∆BFH = ∆CEH (chứng minh câu a)

Suy ra BH = CH (hai cạnh tương ứng)

Do đó H nằm trên trung trực của BC

Mặt khác: AB = AC (chứng minh câu a)

Nên A nằm trên trung trực của BC

Do đó AH là đường trung trực của BC.

Vậy AH là đường trung trực của BC.

Bài 5. Cho ∆ABC vuông tại A có AB = 9 cm; BM là đường trung tuyến và G là trọng tâm của tam giác. Kẻ AH ⊥ BM tại H. Tính AM biết rằng S_DABG = 12 cm².

Hướng dẫn giải

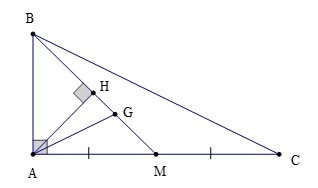
Vì ∆ABC có BM là đường trung tuyến và G là trọng tâm nên ta có: $\text{BG = }\frac{2}{3}\text{BM}$  (1)

Ta có ${\text{S}}_{\mathrm{\Delta ABG}}=\frac{1}{2}\text{AH.BG}$  (2)

${\mathrm{S}}_{\mathrm{\Delta ABM}}=\frac{1}{2}\text{AH.BM}$   (3)

Từ (1), (2) và (3) ta có:

$\frac{{\text{S}}_{\mathrm{\Delta AB}\text{G}}}{{\text{S}}_{\mathrm{\Delta AB}\text{M}}}=$ $\frac{\frac{1}{2}\text{AH.BG}}{\frac{1}{2}\text{AH.BM}}=\frac{\frac{1}{2}\text{AH.}\frac{2}{3}\text{BM}}{\frac{1}{2}\text{AH.BM}}=\frac{2}{3}$

Suy ra 2S_DABM = 3S_DABG

Do đó ${\text{S}}_{\mathrm{\Delta AB}\text{M}}=\frac{3}{2}{\text{S}}_{\mathrm{\Delta AB}\text{G}}=\frac{3}{2}.12=18{\text{(cm}}^2\text{)}$

Ta lại có ${\text{S}}_{\mathrm{\Delta AB}\text{M}}=\frac{1}{2}\text{AB.AM}$ (vì ∆ABM vuông tại A)

Hay $18=\frac{1}{2}\mathrm{.9.}\text{ AM}$ 

Suy ra AM = $\frac{18.2}{9}$= 4 (cm)

Vậy AM = 4 cm.

Bài 6. Cho ∆ABC vuông tại A có I là giao điểm của ba đường phân giác trong tam giác. Gọi E, F là chân các đường vuông góc kẻ từ I đến cạnh AB và AC. Chứng minh IE = IF = EA = FA.

Hướng dẫn giải

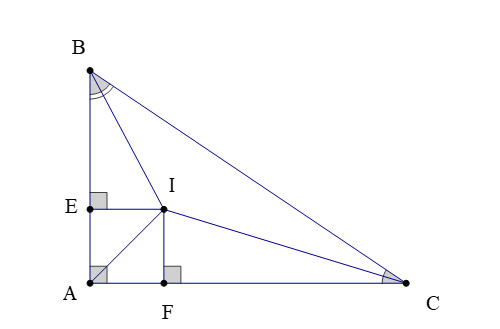
Theo bài ta có: I là giao điểm của ba đường phân giác trong ∆ABC.

Do đó AI là phân giác $\widehat{\text{BAC}}$ hay $\widehat{\text{EAF}}$.

Suy ra $\widehat{\text{EAI}}=\widehat{\text{FAI}}=\frac{1}{2}\widehat{\mathrm{BAC}}$  (tính chất tia phân giác)

Mà $\widehat{\mathrm{BAC}}=90°$ nên $\widehat{\text{EAI}}=\widehat{\text{FAI}}=\frac{90°}{2}=45°$

∆AEI vuông tại E có $\widehat{\text{EAI}}=45°$nên ∆AEI vuông cân tại E.

Suy ra EA = EI (tính chất tam giác cân)         (1)

∆AFI vuông tại F có $\widehat{\text{FAI}}=45°$nên ∆AFI vuông cân tại F.

Suy ra FA = FI (tính chất tam giác cân)         (2)

Do I là giao điểm của ba đường phân giác trong ∆ABC và IE; IF lần lượt là khoảng cách từ I đến cạnh AB; AC (vì E, F là chân các đường vuông góc kẻ từ I đến cạnh AB và AC)

Nên IE = IF (tính chất ba đường phân giác trong tam giác)  (3)

Từ (1), (2) và (3) suy ra IE = IF = EA = FA.

Vậy IE = IF = EA = FA.

Bài 7. Cho ∆ABC cân tại A có đường cao AD. Kẻ DI ⊥ AB tại I, lấy điểm M trên AB sao cho I là trung điểm BM.

a) Chứng minh rằng: $\text{DM = }\frac{1}{2}\text{BC.}$

b) Gọi H là giao điểm của CM và AD. Chứng minh: H là trực tâm của ∆ABC.

Hướng dẫn giải

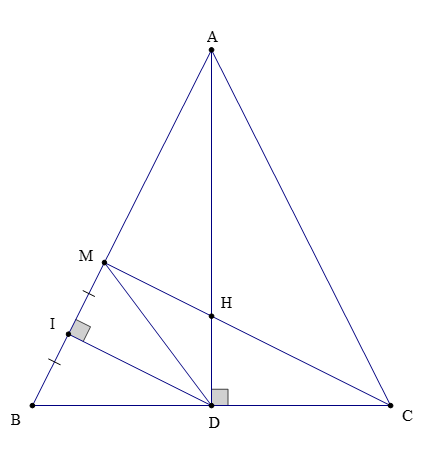
a) Theo bài ta có: DI ⊥ AB tại I mà I là trung điểm của BM (giả thiết)

Do đó DI là trung trực của BM.

Suy ra DB = DM (tính chất đường trung trực của đoạn thẳng)

Xét ∆ABD và ∆ACD có:

$\widehat{\text{ADB}}=\widehat{\text{ADC}}=90°$ (vì AD ⊥ BC tại D),

AB = AC (vì ∆ABC cân tại A),

AD là cạnh chung.

Do đó ∆ABD = ∆ACD (cạnh huyền – cạnh góc vuông)

Suy ra DB = DC (hai cạnh tương ứng)

Suy ra D là trung điểm của BC.

Do đó $\text{BD = }\frac{1}{2}\mathrm{BC}$.

Mà DB = DM (chứng minh trên)

Suy ra $\text{DM = }\frac{1}{2}\text{BC}$

Vậy $\text{DM = }\frac{1}{2}\text{BC}$.

b) Theo phần a ta có : DM = DB = DC

Xét ∆DBM có DM = DB suy ra ∆DBM cân tại D

Do đó $\widehat{\text{DBM}}=\widehat{\text{DMB}}$ (tính chất tam giác cân)  (1)

Xét ∆DMC có DM = DC suy ra ∆DMC cân tại D

Do đó $\widehat{\text{DMC}}=\widehat{\text{DCM}}$ (tính chất tam giác cân)   (2)

Xét ∆BMC có: $\widehat{\text{BMC}}+\widehat{\text{MBC}}+\widehat{\text{MCB}}=180°$(tổng ba góc trong tam giác)

Hay $\widehat{\text{BMC}}+\widehat{\text{MBD}}+\widehat{\text{MCD}}=180°$   (3)

Từ (1), (2) và (3) suy ra $\widehat{\text{BMC}}+\widehat{\text{BMD}}+\widehat{\text{DMC}}=180°$

Hay $\widehat{\text{BMC}}+\widehat{\text{BMC}}=180°$

Suy ra $2\widehat{\text{BMC}}=180°$

Suy ra $\widehat{\text{BMC}}=90°$ 

Do đó CM ⊥ AB tại M.

Hay CM là đường cao của ∆ABC.

Xét ∆ABC có hai đường cao AD và CM cắt nhau tại H.

Suy ra H là trực tâm của ∆ABC (tính chất các đường cao trong tam giác).

Vậy H là trực tâm của ∆ABC.

B.2 Bài tập trắc nghiệm

Câu 1. Cho một tam giác cân có độ dài hai cạnh (không bằng nhau) là 2 cm và 5 cm. Chu vi của tam giác đó là:

A. 9 cm;

B. 10 cm;

C. 11 cm;

D. 12 cm.

Hướng dẫn giải

Đáp án đúng là: D

Giả sử tam giác ABC cân có AB = 2 cm và BC = 5 cm.

Áp dụng bất đẳng thức cho tam giác ABC ta có:

BC – AB < AC < BC + AB

Hay 5 – 2 < AC < 5 + 2

Suy ra 3 < AC < 7              (*)

Vì tam giác ABC là tam giác cân (giả thiết)

Mà AB = 2 cm và BC = 5 cm nên không thể cân tại B.

Do đó có hai trường hợp có thể xảy ra:

• Trường hợp 1: DABC cân tại A.

Suy ra AB = AC.

Mà AB = 2 cm nên AC = 2 cm (không thỏa mãn điều kiện (*))

Nên AB = 2 cm hoặc AB = 5 cm                 (2)

• Trường hợp 2: DABC cân tại C.

Suy ra CA = CB.

Mà BC = 5 cm nên AC = 5 cm (thỏa mãn điều kiện (*))

Vậy AC = 5 cm.

Khi đó chu vi tam giác ABC là:

AB + AC + BC = 2 + 5 + 5 = 12 (cm).

Ta chọn phương án D.

Câu 2. Cho hai tam giác ABC và MNP như hình vẽ dưới đây:

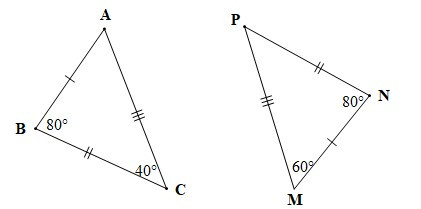
Khẳng định nào sau đây là đúng?

A. DABC = DMNP;

B. DABC = DMPN;

C. DABC = DNMP;

D. DABC = DNPM.

Hướng dẫn giải

Đáp án đúng là: A

Xét tam giác ABC ta có: $\widehat{\mathrm{A}}+\widehat{\mathrm{B}}+\widehat{\mathrm{C}}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{\mathrm{A}}=180°-\widehat{\mathrm{B}}-\widehat{\mathrm{C}}$ 

Hay $\widehat{\mathrm{A}}=180°-80°-40°=60°$ 

Xét tam giác MNP ta có: $\widehat{\mathrm{M}}+\widehat{\mathrm{N}}+\widehat{\mathrm{P}}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{\mathrm{P}}=180°-\widehat{\mathrm{N}}-\widehat{\mathrm{M}}$ 

Hay $\widehat{\mathrm{P}}=180°-80°-60°=40°$ 

Khi đó: tam giác ABC và tam giác MNP có:

+) AB = NM, BC = NP, AC = MP;

+) $\widehat{\mathrm{A}}=\widehat{\mathrm{M}}\left(=60°\right),\widehat{\mathrm{B}}=\widehat{\mathrm{N}}\left(=80°\right),\widehat{\mathrm{C}}=\widehat{\mathrm{P}}\left(=40°\right)$ 

Do đó hai tam giác ABC và MNP bằng nhau và được kí hiệu là DABC = DMNP.

Vậy ta chọn phương án A.

Câu 3. Cho hình vuông ABCD, trên cạnh AD lấy điểm E, trên cạnh DC lấy điểm F và trên cạnh BC lấy điểm G sao cho AE = DF = CG. Số đo góc GFE là:

A. 45°;

B. 90°;

C. 60°;

D. 100°.

Hướng dẫn giải

Đáp án đúng là: B

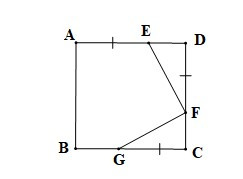
Vì ABCD là hình vuông (giả thiết) nên AD = CD (tính chất hình vuông)

Do đó AE + ED = CF + FD

Mà AE = FD (giả thiết) nên ED = CF.

Xét DFED và DGFC có:

FD = CG (giả thiết),

$\widehat{\mathrm{D}}=\widehat{\mathrm{C}}$ ($=90°,$ tính chất hình vuông),

ED = CF (chứng minh trên)

Do đó DFED = DGFC (hai cạnh góc vuông)

Suy ra $\widehat{\mathrm{F}\text{ED}}=\widehat{\mathrm{CFG}}$ (hai góc tương ứng)

Mà $\widehat{\mathrm{F}\text{ED}}+\widehat{\mathrm{DF}\text{E}}=90°$ (trong tam giác FDE vuông tại D, hai góc nhọn phụ nhau)

Do đó $\widehat{\mathrm{GFC}}+\widehat{\mathrm{DF}\text{E}}=90°$

Mặt khác $\widehat{\mathrm{GFC}}+\widehat{\mathrm{DF}\text{E}}+\widehat{\mathrm{GF}\text{E}}=180°$

Suy ra $\widehat{\mathrm{GF}\text{E}}=180°-\left(\widehat{\mathrm{GFC}}+\widehat{\mathrm{DF}\text{E}}\right)=180°-90°=90°$

Vậy $\widehat{\mathrm{GF}\text{E}}=90°.$ 

Câu 4. Cho ∆ABC vuông tại A có $\widehat{\mathrm{C}}=30°$. Kẻ AH ⊥ BC tại H và tia phân giác AD của $\widehat{\mathrm{HAC}}$ (D ∈ BC). Trên cạnh AC lấy điểm E sao cho AE = AH. Trên tia đối của tia HA lấy điểm F sao cho HF = EC. Khẳng định nào sau đây đúng nhất?

A. ∆ADH = ∆ADE;                  

B. DE ⊥ AC;                   

C. ∆ACF đều;                 

D. Cả A, B, C đều đúng.

Hướng dẫn giải

Đáp án đúng là: D

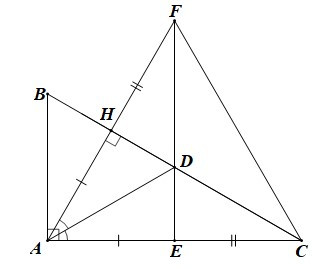
Ta xét từng đáp án:

Đáp án A:

Xét ∆ADH và ∆ADE, có:

AH = AE (giả thiết).

$\widehat{\mathrm{HAD}}=\widehat{\mathrm{DAE}}$ (do AD là phân giác của $\widehat{\mathrm{HAC}}$).

AD là cạnh chung.

Do đó ∆ADH = ∆ADE (c.g.c)

Suy ra đáp án A đúng.

Đáp án B:

∆ADH = ∆ADE (chứng minh trên).

Suy ra $\widehat{\mathrm{AHD}}=\widehat{\mathrm{AED}}$ (cặp góc tương ứng).

Mà $\widehat{\mathrm{AHD}}=90°$ (do AH ⊥ HD).

Do đó $\widehat{\mathrm{AED}}=90°$.

Khi đó ta có DE ⊥ AE hay DE ⊥ AC.

Do đó đáp án B đúng.

Đáp án C:

Ta có AH = AE (giả thiết) và HF = EC (giả thiết).

Suy ra AH + HF = AE + EC.

Do đó AF = AC.

Khi đó ta có ∆ACF cân tại A                          (1).

Vì ∆AHC vuông tại H nên $\widehat{\mathrm{HAC}}+\widehat{\mathrm{HCA}}=90°$.

Do đó $\widehat{\mathrm{HAC}}=90°-\widehat{\mathrm{HCA}}=90°-30°=60°$  (2).

Từ (1), (2), ta suy ra ∆ACF là tam giác đều.

Do đó đáp án C đúng.

Vậy ta chọn đáp án D.

Câu 5. Cho hình vẽ sau:

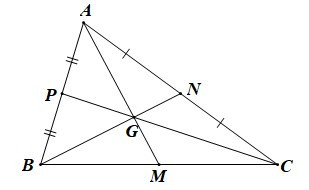
Biết AM = 3 cm. Độ dài đoạn thẳng GM là:

A. 1 cm;

B. 2 cm;

C. 3 cm;

D. 4,5 cm.

Hướng dẫn giải

Đáp án đúng là: A

Trên hình vẽ, hai đường trung tuyến BN và CP cắt nhau tại G

Nên G là trọng tâm tam giác ABC

Do đó $\mathrm{AG}=\frac{2}{3}\mathrm{AM}$(tính chất trọng tâm)

Suy ra $\mathrm{GM}=\frac{1}{3}\mathrm{AM}$

Mà AM = 3 cm

Nên GM = 1 cm.

Vậy ta chọn phương án A.

Câu 6. Giao điểm của ba đường trung tuyến trong một tam giác được gọi là gì?

A. Điểm cách đều ba đỉnh của tam giác đó;            

B. Trọng tâm;                  

C. Điểm cách đều ba cạnh của tam giác đó;            

D. Trực tâm.

Hướng dẫn giải

Đáp án đúng là: B

Điểm cách đều ba đỉnh của tam giác là giao điểm của ba đường trung trực của tam giác đó.

Trọng tâm là giao điểm của ba đường trung tuyến của một tam giác.

Điểm cách đều ba cạnh của tam giác là giao điểm của ba đường phân giác của tam giác đó.

Trực tâm là giao điểm của ba đường cao của một tam giác.

Vậy ta chọn phương án B.

Câu 7. Cho ∆ABC vuông tại A. Trực tâm của ∆ABC là điểm nào?

A. Điểm A;           

B. Điểm B;           

C. Điểm C;           

D. Không có trực tâm.

Hướng dẫn giải

Đáp án đúng là: A

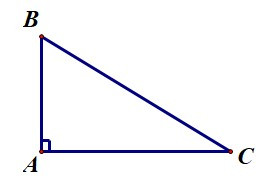
Trong một tam giác, trực tâm là giao điểm của ba đường cao.

Để xác định trực tâm của một tam giác, ta cần xác định giao điểm của ít nhất hai đường cao của tam giác đó.

Vì ∆ABC vuông tại A nên ta có AB ⊥ AC tại A.

Suy ra ∆ABC có hai đường cao là AB và AC.

Hai đường cao này cắt nhau tại A.

Do đó A là trực tâm của ∆ABC.

Vậy ta chọn phương án A.

Câu 8. Cho tam giác ABC (AC < BC), a là đường trung trực của đoạn thẳng AB. Lấy điểm M (M khác trung điểm của AB) nằm trên đường thẳng a.

So sánh độ dài của MA + MC với độ dài đoạn BC.

A. MA + MC < BC;                  

B. MA + MC > BC;                  

C. MA + MC = BC;                  

D. Không thể so sánh được.

Hướng dẫn giải

Đáp án đúng là: B

Vì M nằm trên đường trung trực của đoạn thẳng AB nên MA = MB  (1).

Xét ∆CMB, có: MC + MB > BC (bất đẳng thức tam giác)  (2).

Từ (1), (2), ta suy ra MC + MA > BC.

 Vậy ta chọn phương án B.

Câu 9. Cho ∆ABC vuông cân tại A. Trên cạnh AB lấy điểm D bất kì (D ≠ A, B), trên tia đối của tia AC, lấy điểm E sao cho AD = AE. Khẳng định nào sau đây đúng nhất?

A. $\widehat{\mathrm{ACD}}=\widehat{\mathrm{ABE}}$;             

B. CD ⊥ BE;                   

C. D là trực tâm của ∆BEC;                

D. Cả A, B, C đều đúng.

Hướng dẫn giải

Đáp án đúng là: D

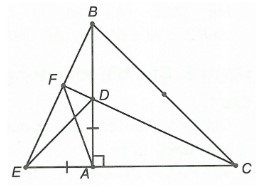
• Xét ∆ABE và ∆ACD, có:

$\widehat{\mathrm{BAE}}=\widehat{\mathrm{CAD}}=90°$,

AE = AD (giả thiết),

AB = AC (do ∆ABC vuông cân tại A).

Do đó ∆ABE = ∆ACD (hai cạnh góc vuông)

Suy ra $\widehat{\mathrm{ACD}}=\widehat{\mathrm{ABE}}$ (cặp góc tương ứng).

Vì vậy đáp án A đúng.

• Gọi F là giao điểm của CD và BE.

Ta có $\widehat{\mathrm{FDB}}=\widehat{\mathrm{ADC}}$ (hai góc đối đỉnh).

Xét ∆ACD vuông tại A có: $\widehat{\mathrm{ADC}}+\widehat{\mathrm{ACD}}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau)

Suy ra $\widehat{\mathrm{FDB}}+\widehat{\mathrm{DBF}}=90°$.

∆DBF có: $\widehat{\mathrm{BFD}}+\widehat{\mathrm{FDB}}+\widehat{\mathrm{DBF}}=180°$ (định lí tổng ba góc của một tam giác)

Suy ra $\widehat{\mathrm{BFD}}=180°-\left(\widehat{\mathrm{FDB}}+\widehat{\mathrm{DBF}}\right)=180°-90°=90°$.

Do đó BF ⊥ FD hay BE ⊥ CD.

Do đó đáp án B đúng.

• Xét ∆BCE có BA, CD là hai đường cao.

Mà BA cắt CD tại D.

Suy ra D là trực tâm của ∆BCE.

Do đó đáp án C đúng.

Vậy ta chọn đáp án D.

Câu 10. Cho hình vẽ sau:

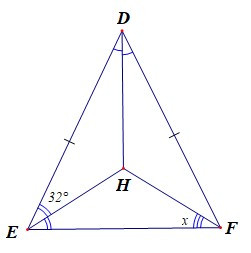
Biết $\widehat{\mathrm{DEH}}=32°.$ Số đo góc x là:

A. x = 26°;            

B. x = 32°;            

C. x = 64°;            

D. x = 128°.

Hướng dẫn giải

Đáp án đúng là: B

• Ta có DE = DF nên ∆DEF cân tại D.

Suy ra $\widehat{\mathrm{DFE}}=\widehat{\mathrm{DEF}}$ (tính chất tam giác cân)

Mà $\widehat{\mathrm{DEH}}=\widehat{\mathrm{HEF}}=32°$

Do đó EH là tia phân giác của $\widehat{\mathrm{DEF}}$

Suy ra $\widehat{\mathrm{DEF}}=2\widehat{\mathrm{DEH}}=2.32°=64°$.

Nên $\widehat{\mathrm{DFE}}=64°$

• ∆DEF có hai đường phân giác DH và EH cắt nhau tại H.

Ta suy ra FH là đường phân giác thứ ba của ∆DEF.

Do đó $\mathrm{x}=\widehat{\mathrm{HFE}}=\frac{1}{2}\widehat{\mathrm{DFE}}=\frac{1}{2}.64°=32°$.

Vậy ta chọn đáp án B.

====== ****&**** =====