a) Tìm số nguyên x, biết: x + 5 = – 3. b) Trong tập hợp các số nguyên, nêu quy tắc tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại.

Câu hỏi:

a) Tìm số nguyên x, biết: x + 5 = – 3.

b) Trong tập hợp các số nguyên, nêu quy tắc tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại.

Trả lời:

a) x + 5 = – 3
x = – 3 – 5
x = – (3 + 5)
x = – 8 (thỏa mãn x là số nguyên).
Vậy x = – 8.
b) Trong tập hợp các số nguyên, muốn tìm một số hạng chưa biết ta lấy tổng của hai số trừ đi số hạng còn lại.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Giải SGK Toán 7 Bài 2 (Cánh diều): Cộng, trừ, nhân, chia số hữu tỉ
   Giải bài tập Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

   Video bài giảng Cộng, trừ, nhân, chia số hữu tỉ – Cánh diều

   I. Cộng, trừ hai số hữu tỉ. Quy tắc chuyển vế.

   Giải Toán 7 trang 12 Tập 1

   Hoạt động 1 trang 12 Toán lớp 7: Thực hiện các phép tính sau:

   a)$\frac{-2}{5}+\frac{3}{7}$;            b)$0,123-0,234$.

   Phương pháp giải:

   a) Quy đồng mẫu hai phân số rồi thực hiện phép cộng hai phân số.           

   b) Áp dụng quy tắc trừ hai số thập phân.

   Lời giải:

   a)$\frac{-2}{5}+\frac{3}{7}=\frac{-14}{35}+\frac{15}{35}=\frac{1}{35}$           

   b)$0,123-0,234=-\left(0,234-0,123\right)=-0,111.$

   Giải Toán 7 trang 13 Tập 1

   Luyện tập vận dụng 1 trang 13 Toán lớp 7: Tính:

   a)$\frac{5}{7}-\left(-3,9\right)$;

   b)$\left(-3,25\right)+4\frac{3}{4}$.

   Phương pháp giải:

   –          Đưa hai số về phép cộng, trừ hai phân số.

   –          Quy đồng mẫu hai phân số rồi thực hiện phép cộng hai phân số.           

   Lời giải chi tiết:

   a)$\frac{5}{7}-\left(-3,9\right)=\frac{5}{7}+3,9=\frac{5}{7}+\frac{39}{10}=\frac{50}{70}+\frac{273}{70}=\frac{323}{70}$;

   b)$\left(-3,25\right)+4\frac{3}{4}=-\frac{13}{4}+\frac{19}{4}=\frac{6}{4}=\frac{3}{2}.$

   Hoạt động 2 trang 13 Toán lớp 7: Nêu tính chất của phép cộng các số nguyên

   Phương pháp giải:

   Nhớ lại tính chất của phép cộng các số nguyên đã học.

   Lời giải:

   Tính chất giao hoán: $a+b=b+a.$

   Tính chất kết hợp: $(a+b)+c=a+(b+c).$

   Cộng với số 0: $a+0=0+a=a$.

   Cộng với số đối: $a+(-a)=0.$

   Luyện tập vận dụng 2 trang 13 Toán lớp 7: Tính một cách hợp lí:

   a)$\left(-0,4\right)+\frac{3}{8}+\left(-0,6\right)$;

   b)$\frac{4}{5}-1,8+0,375+\frac{5}{8}$.

   Phương pháp giải:

   Sử dụng tính chất giao hoán của các số hữu tỉ.

   Lời giải:

   a)$\left(-0,4\right)+\frac{3}{8}+\left(-0,6\right)=\left[\left(-0,4\right)+\left(-0,6\right)\right]+\frac{3}{8}=-1+\frac{3}{8}=\frac{-5}{8}$.

   b)

   $\frac{4}{5}-1,8+0,375+\frac{5}{8}=(0,8-1,8)+(0,375+0,625)=(-1)+1=0$

   Hoạt động 3 trang 13 Toán lớp 7: a) Tìm số nguyên x, biết: $x+5=-3.$

   b) Trong tập hợp các số nguyên, nếu quy tắc tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại.

   Phương pháp giải:

   a) Áp dụng quy tắc tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại.

   b) Nhắc lại quy tắc đã được học

   Lời giải:

   a)

    $\begin{array}{l}x+5=-3\\ x=-3-5\\ x=-8.\end{array}$

   Vậy x=-8.

   b) Quy tắc: Muốn tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại, ta lấy tổng trừ đi số hạng kia.

   Giải Toán 7 trang 14 Tập 1

   Luyện tập vận dụng 3 trang 14 Toán lớp 7: Tìm x, biết:

   a)$x-\left(-\frac{7}{9}\right)=-\frac{5}{6}$;

   b)$\frac{15}{-4}-x=0,3$.

   Phương pháp giải:

   Sử dụng quy tắc chuyển vế.

   Lời giải:

   a)

   $\begin{array}{l}x-\left(-\frac{7}{9}\right)=-\frac{5}{6}\\ x+\frac{7}{9}=-\frac{5}{6}\\ x=-\frac{5}{6}-\frac{7}{9}\\ x=-\frac{15}{18}-\frac{14}{18}\\ x=\frac{-29}{18}\end{array}$

   Vậy $x=\frac{-29}{18}$.

   b)

   $\begin{array}{l}\frac{15}{-4}-x=0,3\\ x=\frac{15}{-4}-0,3\\ x=-3,75-0,3\\ x=-4,05\end{array}$

   Vậy $x=-4,05$.

   II. Nhân, chia hai số hữu tỉ.

   Hoạt động 4 trang 14 Toán lớp 7: Thực hiện các phép tính sau:

   a)$\frac{1}{8}.\frac{3}{5}$            b)$\frac{-6}{7}:\left(-\frac{5}{3}\right);$           c)$0,6.\left(-0,15\right)$.

   Phương pháp giải:

   –          Câu a và b: áp dụng quy tắc nhân, chia hai phân số.

   –          Câu c: Đưa về dạng phép nhân hai phân số, rồi thực hiện phép tính.

   Lời giải:

   a)$\frac{1}{8}.\frac{3}{5}=\frac{1.3}{8.5}=\frac{3}{40}$           

   b)$\frac{-6}{7}:\left(-\frac{5}{3}\right)=\frac{-6}{7}.\frac{-3}{5}=\frac{18}{35}$           

   c)$0,6.\left(-0,15\right)=\frac{6}{10}.\frac{-15}{100}=\frac{-90}{1000}=\frac{-9}{100}$.

   Luyện tập vận dụng 4 trang 14 Toán lớp 7: Giải bài toán nêu trong phần mở đầu.

   Phương pháp giải:

   Độ dài đèo Hải Vân = Độ dài hầm Hải Vân : $\frac{157}{500}$.

   Lời giải:

   Độ dài đèo Hải Vân là:

   $6,28:\frac{157}{500}=\frac{157}{25}.\frac{500}{157}=\frac{3135}{157}\approx 20\left(km\right)$

   Luyện tập vận dụng 5 trang 14 Toán lớp 7:  Một ô tô đi từ tỉnh A đến tỉnh B. Trong 1 giờ đầu, ô tô đã đi được $\frac{2}{5}$ quãng đường. Hỏi với vận tốc đó, ô tô phải mất bao lâu để đi hết quãng đường AB?

   Phương pháp giải:

   Thời gian ô tô đi hết cả quãng đường AB = Thời gian đi : Quãng đường đi được.

   Lời giải:

   Thời gian ô tô đi hết quãng đường AB là: $1:\frac{2}{5}=\frac{5}{2}$(h)

   Giải Toán 7 trang 15 Tập 1

   Hoạt động 5 trang 15 Toán lớp 7: Nêu tính chất của phép nhân các số nguyên.

   Phương pháp giải:

   Nhớ lại tính chất của phép nhân các số nguyên đã học.

   Lời giải:

   Tính chất giao hoán: $a.b=b.a.$

   Tính chất kết hợp: $(a.b).c=a.(b.c).$

   Nhân với số 1: $a.1=1.a=a$.

   Tính chất phân phối của phép nhân đối với phép cộng: $a.(b+c)=a.b+a.c.$

   Luyện tập vận dụng 6 trang 15 Toán lớp 7: Tính một cách hợp lí:

   a)$\frac{7}{3}.\left(-2,5\right).\frac{6}{7};$

   b)$0,8.\frac{-2}{9}-\frac{4}{5}.\frac{7}{9}=0,2.$

   Phương pháp giải:

   Tính chất giao hoán: $a.b=b.a.$

   Tính chất kết hợp: $(a.b).c=a.(b.c).$

   Tính chất phân phối của phép nhân đối với phép trừ: $a.(b-c)=a.b-a.c.$

   Lời giải:

   a)$\frac{7}{3}.\left(-2,5\right).\frac{6}{7}=\frac{7}{3}.\frac{6}{7}.\left(-2,5\right)=2.\left(-2,5\right)=-5$

   b)

   $\begin{array}{l}0,8.\frac{-2}{9}-\frac{4}{5}.\frac{7}{9}=0,2=\frac{4}{5}.\frac{-2}{9}-\frac{4}{5}.\frac{7}{9}\\ =\frac{4}{5}.\left(\frac{-2}{9}-\frac{7}{9}\right)=\frac{4}{5}.\left(-1\right)=\frac{-4}{5}.\end{array}$

   Hoạt động 6 trang 15 Toán lớp 7: Nêu phân số nghịch đảo của phân số $\frac{m}{n}$ $\left(m\ne 0;n\ne 0\right)$.

   Phương pháp giải:

   Phân số cần tìm là phân số nhân với phân số $\frac{m}{n}$ được tích bằng 1.

   Lời giải:

   Phân số nghịch đảo của phân số $\frac{m}{n}$ là: $\frac{n}{m}$

   Giải Toán 7 trang 16 Tập 1

   Luyện tập vận dụng 7 trang 16 Toán lớp 7: Tìm số nghịch đảo của mỗi số hữu tỉ sau:

   a)$2\frac{1}{5}$;                    b)$-13$

   Phương pháp giải:

   a)Đưa hỗn số về phân số rồi tìm số nghịch đảo

   Phân số nghịch đảo của phân số $\frac{m}{n}$ là: $\frac{n}{m}$$\left(m\ne 0;n\ne 0\right)$

   b) Số nghịch đảo của số a là: $\frac{1}{a}\left(a\ne 0\right)$.

   Lời giải:

   a)Ta có: $2\frac{1}{5}=\frac{11}{5}$

   Số nghịch đảo của $2\frac{1}{5}$ là: $\frac{5}{11}$.

   b) Số nghịch đảo của $-13$ là: $\frac{-1}{13}$

   Chú ý: Ta phải chuyển hỗn số về phân số trước khi tìm số nghịch đảo.

   Bài tập.

   Bài 1 trang 16 Toán lớp 7: Tính:

   a)$\frac{-1}{6}+0,75$;          b)$3\frac{1}{10}-\frac{3}{8}$;               c)$0,1+\frac{-9}{17}-\left(-0,9\right)$.

   Phương pháp giải: 

   Đưa các phép tính về phép cộng, trừ các phân số.

   Áp dụng tính chất giao hoán và kết hợp để tính nhanh (nếu có thể).

   Lời giải:

   a)$\frac{-1}{6}+0,75=\frac{-1}{6}+\frac{3}{4}=\frac{-2}{12}+\frac{9}{12}=\frac{7}{12}.$;         

   b)$3\frac{1}{10}-\frac{3}{8}=\frac{31}{10}-\frac{3}{8}=\frac{124}{40}-\frac{15}{40}=\frac{109}{40}$;              

   c)

   $\begin{array}{l}0,1+\frac{-9}{17}-\left(-0,9\right)=\frac{1}{10}+\frac{-9}{17}+\frac{9}{10}\\ =\frac{1}{10}+\frac{9}{10}+\frac{-9}{17}=1+\frac{-9}{17}=\frac{8}{17}\end{array}$

   Bài 2 trang 16 Toán lớp 7: Tính:

   a)$5,75.\frac{-8}{9}$;               b)$2\frac{3}{8}.\left(-0,4\right)$;             c)$\frac{-12}{5}:\left(-6,5\right)$.

   Phương pháp giải:

   Đưa về phép nhân, chia các phân số.

   Lời giải:

   a)$5,75.\frac{-8}{9}=\frac{23}{4}.\frac{-8}{9}=\frac{-46}{9}$$5,75.\frac{-8}{9}=\frac{23}{4}.\frac{-8}{9}=\frac{-46}{9}$        

   b)$2\frac{3}{8}.\left(-0,4\right)=\frac{19}{8}.\frac{-2}{5}=\frac{-19}{20}$;            

   c)$\frac{-12}{5}:\left(-6,5\right)=\frac{-12}{5}:\frac{-13}{2}=\frac{-12}{5}.\frac{-2}{13}=\frac{24}{65}$

   Bài 3 trang 16 Toán lớp 7: Tính một cách hợp lí:

   a)$\frac{-3}{10}-0,125+\frac{-7}{10}+1,125$;            b)$\frac{-8}{3}.\frac{2}{11}-\frac{8}{3}:\frac{11}{9}$;

   Phương pháp giải: 

   a)      Áp dụng tính chất giao hoán và kết hợp của phép cộng.

   b)      Áp dụng tính chất phân phối của phép nhân đối với phép cộng: $a.(b+c)=a.b+a.c.$

   Lời giải:

   a)

   $\begin{array}{l}\frac{-3}{10}-0,125+\frac{-7}{10}+1,125=\left(\frac{-3}{10}+\frac{-7}{10}\right)+\left(1,125-0,125\right)\\ =-1+1=0\end{array}$       

   b)

   $\begin{array}{l}\frac{-8}{3}.\frac{2}{11}-\frac{8}{3}:\frac{11}{9}=\frac{8}{3}.\frac{-2}{11}-\frac{8}{3}.\frac{9}{11}\\ =\frac{8}{3}.\left(\frac{-2}{11}-\frac{9}{11}\right)=\frac{8}{3}.\left(-1\right)=\frac{-8}{3}\end{array}$

   Bài 4 trang 16 Toán lớp 7: Tìm x, biết:

   a)$x+\left(-\frac{1}{5}\right)=\frac{-4}{15}$;                         

   b)$3,7-x=\frac{7}{10};$

   c)$x.\frac{3}{2}=2,4$;                                  

   d)$3,2:x=-\frac{6}{11}$.

   Phương pháp giải:

   Sử dụng quy tắc chuyển vế đổi dấu để tìm x.

   Lời giải:

   a)

   $\begin{array}{l}x+\left(-\frac{1}{5}\right)=\frac{-4}{15}\\ x=\frac{-4}{15}+\frac{1}{5}\\ x=\frac{-4}{15}+\frac{3}{15}\\ x=\frac{-1}{15}\end{array}$                 

   Vậy $x=\frac{-1}{15}$.

   b)

   $\begin{array}{l}3,7-x=\frac{7}{10}\\ x=3,7-\frac{7}{10}\\ x=\frac{37}{10}-\frac{7}{10}\\ x=3\end{array}$

   Vậy $x=3$.

   c)

   $\begin{array}{l}x.\frac{3}{2}=2,4\\ x.\frac{3}{2}=\frac{12}{5}\\ x=\frac{12}{5}:\frac{3}{2}\\ x=\frac{12}{5}.\frac{2}{3}\\ x=\frac{8}{5}\end{array}$$\begin{array}{l}x.\frac{3}{2}=2,4\\ x.\frac{3}{2}=\frac{12}{5}\\ x=\frac{12}{5}:\frac{3}{2}\\ x=\frac{12}{5}.\frac{2}{3}\\ x=\frac{8}{5}\end{array}$           

   Vậy $x=\frac{8}{5}$       

   d)

   $\begin{array}{l}3,2:x=-\frac{6}{11}\\ \frac{16}{5}:x=-\frac{6}{11}\\ x=\frac{16}{5}:\left(-\frac{6}{11}\right)\\ x=\frac{16}{5}.\frac{-11}{6}\\ x=\frac{-88}{15}\end{array}$

   Vậy $x=\frac{-88}{15}$.

   Bài 5 trang 16 Toán lớp 7: Bác Nhi gửi vào ngân hàng 60 triệu đồng với kì hạn 1 năm, lãi suất 6,5%/năm. Hết kì hạn 1 năm, bác rút ra $\frac{1}{3}$ số tiền (kể cả gốc và lãi). Tính số tiền còn lại của bác Nhi trong ngân hàng.

   Phương pháp giải:

   –          Tính số tiền lãi = Số tiền gốc.$\frac{6,5}{100}$

   –          Tính số tiền rút ra

   –          Tính số tiền còn lại.

   Lời giải:

   Số tiền lãi là: $60.\frac{6,5}{100}=3,9$(triệu đồng)

   Số tiền gốc và lãi của bác Nhi sau 1 năm là:

   60 + 3,9 = 63,9 (triệu đồng)

   Số tiền bác Nhi rút ra là:  $\frac{1}{3}$. 63,9 = 21,3 (triệu đồng)

   Số tiền còn lại của bác Nhi trong ngân hàng là: 63,9 – 21,3 = 42,6 (triệu đồng).

   Bài 6 trang 16 Toán lớp 7:Tính diện tích mặt bằng của ngôi nhà được mô tả như Hình 7 (các số đo trên hình tính theo đơn vị mét):

   

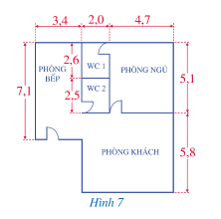
   Phương pháp giải: 

   Chia hình thành hai hình chữ nhật rồi tính tổng hai diện tích hai hình chữ nhật đó.

   Lời giải:

   Diện tích mặt bằng của ngôi nhà là:

   $7,1.3,4+(2,0+4,7).(5,1+5,8)=97,17$(m²)

   Bài 7 trang 16 Toán lớp 7: Theo yêu cầu của kiến trúc sư, ổ cắm điện và vòi nước của nhà chú Năm cách nhau tối thiểu là 60 cm. Trên bản vẽ có tỉ lệ 1 : 20 của thiết kế nhà chú Năm, khoảng cách từ ổ cắm điện đến vòi nước đo được là 2,5 cm. Khoảng cách trên bản vẽ như vậy có phù hợp với yêu cầu của kiến trúc sư không ? Giải thích vì sao.

   Phương pháp giải:

   Tính khoảng cách thực tế từ ổ cắm điện đến vòi nước, theo bản đồ: Khoảng cách trên bản đồ:tỉ lệ

   =>So sánh với khoảng cách và kết luận.

   Lời giải:

   Theo bản đồ, khoảng cách thực tế từ ổ cắm điện đến vòi nước là:

   $2,5:\frac{1}{20}=50$(cm)

   Vì 50 cm <  60 cm nên khoảng cách trên bản vẽ như vậy không phù hợp với yêu cầu của kiến trúc sư.

   Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

   Bài 1: Tập hợp Q các số hữu tỉ

   Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

   Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc

   Bài 5: Biểu diễn thập phân của một số hữu tỉ
2. Sách bài tập Toán 7 Bài 2 (Cánh diều): Cộng, trừ, nhân, chia số hữu tỉ
   Giải SBT Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

   Giải trang 13 Tập 1

   Bài 11 trang 13 Tập 1: Tính:

   a) −6,07 + 3,58;

   b) $\frac{3}{5}+\left(-4\right)$;

   c) $1\frac{3}{5}-\frac{-7}{11}$;

   d) $\frac{-7}{13}+0,6$;

   e) $-1,221.\frac{2}{-5}$;

   g) $\frac{-17}{7}:0,25$.

   Lời giải:

   a) −6,07 + 3,58 = −(6,07 − 3,58) = −2,49;

   b) $\frac{3}{5}+\left(-4\right)$= 0,6 + (−4)

   = −(4 – 0,6) = −3,4;

   

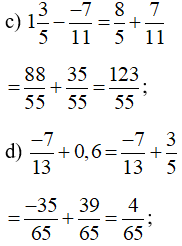
   e) $-1,221.\frac{2}{-5}$ = 1,221 . 0,4 = 0,4884;

   g) $\frac{-17}{7}:0,25=\frac{-17}{7}:\frac{1}{4}$

   $=\frac{-17}{7}.4=\frac{-68}{7}$.

   Bài 12 trang 13 Tập 1: So sánh giá trị của các biểu thức sau:

   $A=10\frac{5}{7}.(-0,7)$; $B=2\frac{4}{5}:(-0,4)$; $C=(-4,5).1\frac{31}{45}$.

   Lời giải:

   Ta có:

   

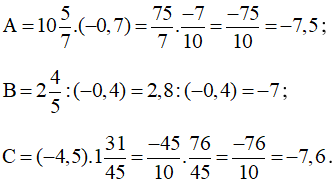
   Vì −7,6 < −7,5 < −7 nên ta có: A < A < B.

   Bài 13 trang 13 Tập 1: Tính một cách hợp lí:

   

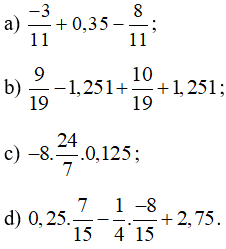
   Lời giải:

   

   

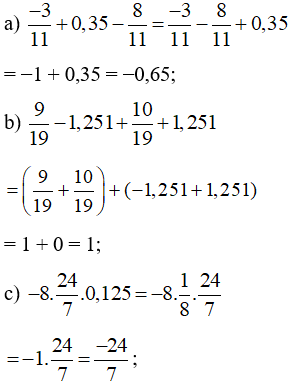
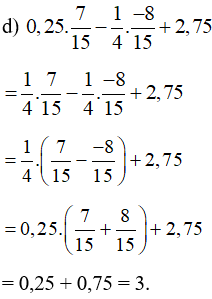
   Bài 14 trang 13 Tập 1: Tìm số hữu tỉ x, biết:

   

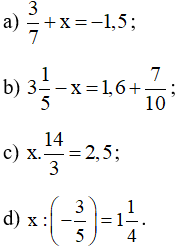
   Lời giải:

   

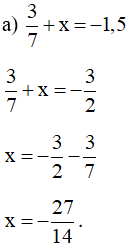
   Vậy $x=-\frac{27}{14}$.

   b) $3\frac{1}{5}-x=1,6+\frac{7}{10}$

   3,2 – x = 1,6 + 0,7

   3,2 – x = 2,3

   x = 3,2 – 2,3

   x = 0,9.

   Vậy x = 0,9.

   

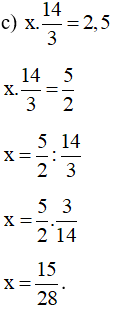
   Vậy $x=\frac{15}{28}$.

   

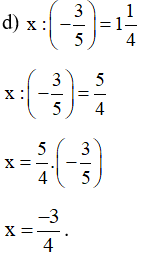
   Vậy $x=\frac{-3}{4}$.

   Giải trang 14 Tập 1

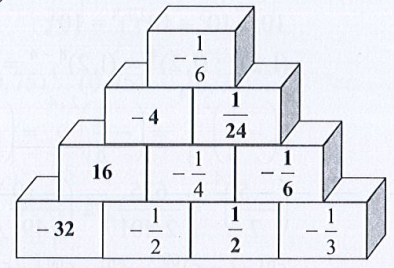
   Bài 15 trang 14 Tập 1: Tìm số thích hợp cho $?$ trong các hình tháp dưới đây theo quy tắc.

   Quy tắc 1:

   

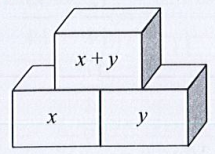
   Quy tắc 2:

   

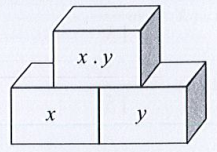
   a) Áp dụng Quy tắc 1, ta có tháp:

   

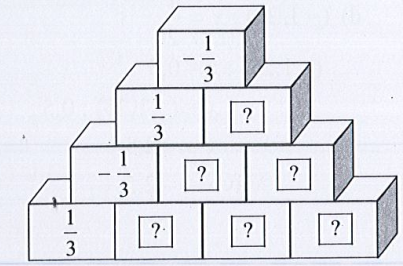
   b) Áp dụng Quy tắc 2, ta có tháp:

   

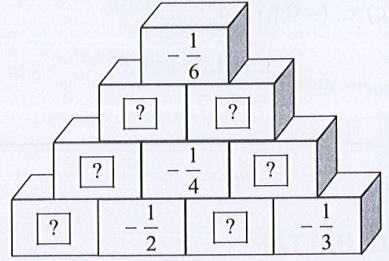
   Lời giải:

   a) Áp dụng Quy tắc 1 thì tổng của hai ô trống bên dưới bằng ô phía trên liền với 2 ô đó.

   Chẳng hạn ta tính:

   ∙ $\frac{1}{3}+?=-\frac{1}{3}$

   Do đó $?=-\frac{1}{3}-\frac{1}{3}=-\frac{2}{3}$;

   ∙ $-\frac{1}{3}+?=\frac{1}{3}$

   Do đó $?=\frac{1}{3}-\left(-\frac{1}{3}\right)=\frac{1}{3}+\frac{1}{3}=\frac{2}{3}$;

   Tương tự ta tính được các ô trống còn lại.

   Ta điền các số vào tháp như sau:

   

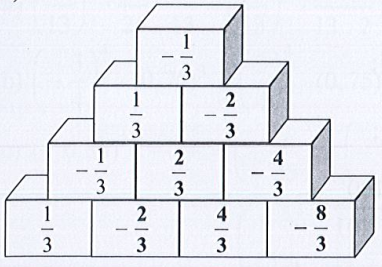
   b) Áp dụng Quy tắc 2 thì tổng của hai ô trống bên dưới bằng ô phía trên liền với 2 ô đó.

   Chẳng hạn ta tính:

   ∙ $-\frac{1}{2}.?=-\frac{1}{4}$

   Do đó

    

   

    

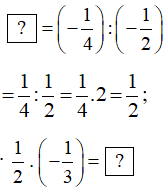
   Do đó .

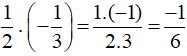   Tương tự ta tính được các ô trống còn lại.

   Ta điền các số vào tháp như sau:

   

   Bài 16 trang 14 Tập 1: Một vệ tinh nhân tạo bay xung quanh Trái Đất ở độ cao 330 km so với mặt đất. Hỏi sau khi bay được đúng một vòng quanh Trái Đất thì vệ tinh đã bay được khoảng bao nhiêu ki-lô-mét? Biết rằng bán kính Trái Đất xấp xỉ 6 371 km (lấy π =3,14).

   Lời giải:

   Khi quanh xung quanh Trái Đất, vệ tinh nhân tạo di chuyển theo một đường tròn có bán kính khoảng:

   6 371 + 330 = 6 701 (km).

   Sau khi bay đúng một vòng Trái Đất thì vệ tinh bay được khoảng:

   2 . 3,14 . 6 701 = 42 082,28 (km).

   Vậy sau khi bay được đúng một vòng quanh Trái Đất thì vệ tinh đã bay được khoảng 42 082,28 ki-lô-mét.

   Bài 17 trang 14 Tập 1: Mẹ bạn Ngân gửi vào ngân hàng 20 triệu đồng với kì hạn 1 năm, lãi suất 7,8%/năm.

   a) Tính số tiền cả gốc và lãi của mẹ bạn Ngân rút ra sau khi hết kì hạn 1 năm.

   b) Sau kì hạn 1 năm, mẹ bạn Ngân rút ra $\frac{3}{40}$ số tiền (cả gốc và lãi) để mua một chiếc xe đạp thưởng cho bạn Ngân vì kết quả học tập đạt mức Tốt. Tính giá của chiếc xe đạp mà mẹ bạn Ngân đã mua.

   Lời giải:

   Mẹ bạn Ngân gửi vào ngân hàng 20 triệu đồng tức là mẹ bạn Ngân gửi vào ngân hàng 20 000 000 đồng.

   a) Số tiền lãi mẹ bạn Ngân nhận được sau kì hạn 1 năm là:

   20 000 000 . 7,8%  = 21 560 000 (đồng).

   Vậy số tiền cả gốc và lãi của mẹ bạn Ngân rút ra sau khi hết kì hạn 1 năm là 21 560 000 đồng.

   b) Giá của chiếc xe đạp mà mẹ bạn Ngân đã mua là:

   $21560000.\frac{3}{40}=1617000$ (đồng).

   Vậy giá của chiếc xe đạp mà mẹ bạn Ngân đã mua 1 617 000 đồng.

   Bài 18 trang 14 Tập 1: Một chiếc máy tính có giá niêm yết là 14 triệu đồng (đã bao gồm thuế VAT). Trong tuần lễ khai trương cửa hàng, chiếc máy tính đó được giảm giá 10% của giá niêm yết và nếu khách hàng mua hàng trực tuyến (giao hàng miễn phí) thì được giảm thêm 5% của giá niêm yết. Tính số tiền bác Lan phải trả khi mua hàng trực tuyến chiếc máy tính đó trong tuần lễ khai trương cửa hàng.

   Lời giải:

   Giá của chiếc máy tính khi mua hàng trực tuyến trong tuần lễ khai trương cửa hàng bằng:

   100% − 10% − 5% = 85% (giá niêm yết).

   Số tiền của bác Lan phải trả khi mua hàng trực tuyến chiếc máy tính đó trong tuần lễ khai trương cửa hàng là:

   14 000 000 . 85% = 11 900 000 (đồng).

   Vậy số tiền bác Lan phải trả khi mua hàng trực tuyến chiếc máy tính đó trong tuần lễ khai trương cửa hàng 11 900 000 đồng.

   Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

   Bài 1: Tập hợp Q các số hữu tỉ

   Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

   Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

   Bài 4: Thứ tự thực hiện phép tính. Quy tắc dấu ngoặc

   Bài 5: Biểu diễn thập phân của số hữu tỉ
3. 20 Bài tập Cộng, trừ, nhân, chia số hữu tỉ có đáp án – Toán 7
   Bài tập Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

   A. Bài tập Cộng, trừ, nhân, chia số hữu tỉ

   A.1 Bài tập tự luận

   Bài 2. Tìm x, biết

   a)  $x+\frac{-1}{3}=\frac{4}{15}$;

   b) $x\cdot \frac{3}{2}=2,4$ .

   Hướng dẫn giải

    a)  $x+\frac{-1}{3}=\frac{4}{15}$ 

   $\text{x =}\frac{4}{15}-\frac{-1}{3}$ 

   $\text{x = }\frac{4}{15}-\frac{-5}{15}$    

   $x=\frac{9}{15}$

   $\text{x = }\frac{3}{5}$

   Vậy $\text{x = }\frac{3}{5}$ .

   b) $x\cdot \frac{3}{2}=2,4$

   $x=2,4:\frac{3}{2}$

   $x=2,4:1,5$

   $x=1,6$

   Vậy x = 1,6.

   Bài 2. Tính

   a) $\frac{-1}{4}+\frac{-1}{3}$ ;

   b) $\frac{-2}{5}-\frac{3}{11}$ ;

   c)  $\frac{-5}{9}:\frac{-7}{18}$;

   d) $\frac{-4}{9}\cdot 0,75$ .

   Hướng dẫn giải

   a) $\frac{-1}{4}+\frac{-1}{3}=\frac{-3}{12}+\frac{-4}{12}=\frac{-7}{12}$ .

   b) $\frac{-2}{5}-\frac{3}{11}=\frac{-22}{55}-\frac{15}{55}=\frac{-37}{55}$ .

   c) $\frac{-5}{9}:\frac{-7}{18}=\frac{-5}{9}\cdot \frac{18}{-7}=\frac{-10}{-7}=\frac{10}{7}$ .

   d) Ta viết $0,75=\frac{75}{100}=\frac{3}{4}$ .

   Khi đó: $\frac{-4}{9}\cdot 0,75=\frac{-4}{9}\cdot \frac{3}{4}=\frac{-1}{3}$ .

   A.2 Bài tập trắc nghiệm

   Câu 1. Thực hiện phép tính $\frac{1}{3}\text{ : }\left(-\text{ 0,125}\right)$ ta được kết quả là:

   A. $\frac{8}{3};$

   B. 2,6;

   C. $-\frac{3}{8};$

   D. $\frac{-\text{ 8}}{3}.$

   Hướng dẫn giải

   Đáp án đúng là: D

   Ta có: $-\text{ 0,125 = }\frac{-\text{ 125}}{1000}\text{ =}\frac{\left(-125\right):125}{1000:125}\text{= }\frac{-\text{ 1}}{8}$ .

   Nên $\frac{1}{3}\text{ : }\left(-\text{ 0,125}\right)\text{ = }\frac{1}{3}\text{ : }\left(\frac{-\text{ 1}}{8}\right)$   

   $=\frac{1}{3}\text{ . }\frac{\text{ 8}}{-1}\text{ = }\frac{\text{1 . 8}}{3.\left(-1\right)}=\frac{8}{-3}=\frac{-8}{3}.$

    

   Câu 2. Cho biết $\text{x + }\frac{2}{15}\text{ = }-\frac{3}{10}$ thì:

   A. $\text{x = }\frac{-\text{ 13}}{30};$

   B. $\text{x = }\frac{11}{30};$

   C. $\text{x = }\frac{-5}{150};$

   D. $\text{x = }\frac{65}{150}.$

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: $x\text{ + }\frac{2}{15}\text{ = }-\frac{3}{10}$

   $x\text{ = }-\frac{3}{10}-\frac{2}{15}$

   $x\text{ = }\frac{-\text{ 9}}{30}-\frac{4}{30}$

   $x\text{ = }\frac{-\text{ 9 }-\text{ 4}}{30}$

   $x\text{ = }\frac{-\text{ 13}}{30}.$

   Vậy $x\text{ = }\frac{-\text{ 13}}{30}.$

   Câu 3. Một ô tô đi từ A đến B với vận tốc 50,5 km/giờ mất 1 giờ 30 phút. Một chiếc xe máy đi với vận tốc bằng $\frac{5}{6}$ vận tốc của ô tô thì sau bao lâu sẽ đi hết quãng đường AB?

   A. $\frac{9}{5}$ giờ;

   B.$\frac{3}{2}$ giờ;

   C. $\frac{4}{3}$ giờ;

   D. 2 giờ.

   Hướng dẫn giải

   Đáp án đúng là: A.

   Đổi: 1 giờ 30 phút = 1$\frac{1}{2}$  giờ = $\frac{3}{2}$ giờ;

   Quãng đường AB dài số ki-lô-mét là:

   $50,5\text{ . }\frac{3}{2}\text{ = }\frac{101}{2}\text{ . }\frac{3}{2}\text{ = }\frac{303}{4}$ (km);

   Vận tốc của xe máy là:

   $50,5\text{ . }\frac{5}{6}\text{ = }\frac{101}{2}\text{ . }\frac{5}{6}\text{ = }\frac{505}{12}$ (km/giờ);

   Thời gian xe máy đi hết quãng đường AB là:

   $\frac{303}{4}\text{ : }\frac{505}{12}\text{ = }\frac{303}{4}\text{ . }\frac{12}{505}\text{ =}\frac{3.101}{4}\text{.}\frac{3.4}{5.101}\text{= }\frac{9}{5}$ (giờ).

   B. Lý thuyết Cộng, trừ, nhân, chia số hữu tỉ

   1. Cộng, trừ hai số hữu tỉ. Quy tắc chuyển vế

   1.1 Quy tắc cộng, trừ hai số hữu tỉ

   – Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

   – Nếu hai số hữu tỉ cùng được viết dưới dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể cộng, trừ hai số đó theo quy tắc cộng, trừ số thập phân.

   Ví dụ: Tính

   a)  $0,5+\frac{-2}{3}$;                              

   b) 1,205 – 2,31.

   Hướng dẫn giải 

   a) Ta có $0,5=\frac{5}{10}=\frac{1}{2}$ . Do đó:

   $0,5+\frac{-2}{3}=\frac{1}{2}+\frac{-2}{3}=\frac{1.3}{2.3}+\frac{(-2).2}{3.2}\text{=}\frac{3}{6}+\frac{-4}{6}=\frac{3+(-4)}{6}=\frac{-1}{6}$.

   b) 1,205 – 2,31= 1,205 + (–2,31) = – (2,31 – 1,205) = –1,105.

   1.2 Tính chất của phép cộng các số hữu tỉ

   – Phép cộng các số hữu tỉ có các tính chất giống với phép cộng các số nguyên: giao hoán, kết hợp, cộng với số 0, cộng với số đối.

   – Ta có thể chuyển phép trừ cho một số hữu tỉ thành phép cộng với số đối của số hữu tỉ đó. Vì thế, trong một biểu thức chỉ có phép cộng và phép trừ, ta có thể thay đổi tùy ý vị trí các số hạng kèm theo dấu của chúng.

   Ví dụ: Tính một cách hợp lý $(-0,4)+\frac{3}{8}+(-0,6)$

   Ta có: $(-0,4)+\frac{3}{8}+(-0,6)=(-0,4)+(-0,6)+\frac{3}{8}=-1+\frac{3}{8}=\frac{-8}{8}+\frac{3}{8}=\frac{-5}{8}$

   1.3 Quy tắc chuyển vế

   Khi chuyển một số hạng tử vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó:

   x + y = z ⇒ x = z – y

   x – y = z ⇒ x = z + y

   Ví dụ: Tìm x, biết

   a) $x-\left(-\frac{7}{9}\right)=-\frac{5}{6}$;                                                           

   b) $\frac{15}{-2}-x=0,3$.

   Hướng dẫn giải

   a) $x-\left(-\frac{7}{9}\right)=-\frac{5}{6}$      

    $\text{x = }\left(-\frac{5}{6}\right)+\left(-\frac{7}{9}\right)$

    $\text{x =}\left(-\frac{15}{18}\right)+\left(-\frac{14}{18}\right)$

    $\text{ x = }-\frac{29}{18}$

   Vậy $\text{ x = }-\frac{29}{18}$ .  

   $b) \frac{15}{-2}-x=0,3$       

   $\frac{15}{-2}-0,3=x$         

   $\text{ x = }\frac{15}{-2}-0,3$

   $\text{x = }-7,8$                 

   Vậy x = – 7,8.

   2. Nhân, chia hai số hữu tỉ

   2.1 Quy tắc nhân, chia hai số hữu tỉ

   – Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

   – Nếu hai số hữu tỉ cùng viết ở dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể nhân, chia hai số đó theo quy tắc nhân, chia số thập phân.

   Ví dụ:

   a) $2\frac{3}{8}:(-0,4)$ ;

   b) $\frac{-12}{5}\cdot (-6,5)$ .

   Hướng dẫn giải

   a) Ta viết $2\frac{3}{8}=\frac{19}{8}$và $-0,4=\frac{-4}{10}=\frac{-2}{5}$

   Khi đó: $2\frac{3}{8}:(-0,4)=\frac{19}{8}:\frac{-2}{5}=\frac{19}{8}\cdot \frac{5}{-2}=\frac{95}{-16}$

   b) Ta có thể viết $-\frac{12}{5}=-\frac{24}{10}=-2,4$

   Khi đó $\frac{-12}{5}\cdot (-6,5)=(-2,4).(-6,5)=15,6$ .

   2.2 Tính chất của phép nhân các số hữu tỉ

   Giống như phép nhân các số nguyên, phép nhân các số hữu tỉ có các tính chất: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân đối với phép cộng và phép trừ.

   Ví dụ: Tính một cách hợp lý:

   a) $\frac{7}{3}\cdot (-2,5)\cdot \frac{6}{7}$ ;

   b) $0,5\cdot \left(\frac{2}{7}+\frac{2}{-3}\right)$ .

   Hướng dẫn giải

   a) $\frac{7}{3}\cdot (-2,5)\cdot \frac{6}{7}=\frac{7}{3}\cdot \frac{6}{7}\cdot (-2,5)=2\cdot (-2,5)=-5$

   b) Ta có $0,5=\frac{5}{10}=\frac{1}{2}$ . Khi đó: 

   $0,5\cdot \left(\frac{2}{7}+\frac{2}{-3}\right)=\frac{1}{2}\cdot \left(\frac{2}{7}+\frac{2}{-3}\right)=\frac{1}{2}\cdot \frac{2}{7}+\frac{1}{2}\cdot \frac{2}{-3}=\frac{1}{7}+\frac{1}{-3}=\frac{3}{21}+\frac{-7}{21}=\frac{-4}{21}$.

   Nhận xét:

   – Số nghịch đảo của số hữu tỉ a khác 0 kí hiệu là $\frac{1}{a}$ . Ta có $a.\frac{1}{a}=1$

   – Số nghịch đảo của số hữu tỉ $\frac{1}{a}$ là a.

   – Nếu a, b là hai số hữu tỉ và b ≠ 0 thì $a:b=a\cdot \frac{1}{b}$.

   Ví dụ:

   Số nghịch đảo của $\frac{-3}{5}$ là $1:\frac{-3}{5}=\frac{5}{-3}=\frac{-5}{3}$

   Số nghịch đảo của 0,3 là $1:0,3=1:\frac{3}{10}=\frac{10}{3}$ .
4. 20 câu Trắc nghiệm Cộng, trừ, nhân, chia số hữu tỉ (Cánh diều) có đáp án 2023 – Toán lớp 7
   Trắc nghiệm Toán 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

   Câu 1. Thực hiện phép tính $\frac{1}{3}\text{:}\left(-\text{0,125}\right)$ ta được kết quả là:

   A.$\frac{8}{3};$

   B. 2,6;

   C.$-\frac{3}{8};$

   D.$\frac{-\text{8}}{3}.$

   Hướng dẫn giải

   Đáp án đúng là: D

   Ta có: $-\text{0,125 =}\frac{-\text{125}}{1000}\text{=}\frac{\left(-125\right):125}{1000:125}\text{=}\frac{-\text{1}}{8}$ .

   Nên $\frac{1}{3}\text{:}\left(-\text{0,125}\right)\text{=}\frac{1}{3}\text{:}\left(\frac{-\text{1}}{8}\right)$

   $=\frac{1}{3}\text{.}\frac{\text{8}}{-1}\text{=}\frac{\text{1 . 8}}{3.\left(-1\right)}=\frac{8}{-3}=\frac{-8}{3}.$

   Câu 2. Tìm x, biết $\text{x : 0,112 =}\frac{1}{5}$

   A. 0,022;

   B. 0,0224;

   C. 0,0448;

   D. 0,044.

   Hướng dẫn giải

   Đáp án đúng là: B

   Ta có: $x\text{: 0,112 =}\frac{1}{5}$

   $x\text{=}\frac{1}{5}\text{. 0,112}$

   $x\text{= 0,2 . 0,112}$

   $x\text{= 0,0224.}$

   Vậy $\text{x = 0,0224.}$

   Câu 3. Số nào sau đây là kết quả của phép tính $1\frac{3}{5}\text{+ 0,45 .}\frac{2}{5}$

   A. 1,77;

   B.$\frac{89}{50};$

   C.$\frac{17}{50};$

   D. 1,7.

   Hướng dẫn giải

   Đáp án đúng là: B

   Ta có: $1\frac{3}{5}\text{=}\frac{8}{5};\text{0,45 =}\frac{45}{100}\text{=}\frac{9}{20}.$

   Do đó: $1\frac{3}{5}\text{+ 0,45 .}\frac{2}{5}\text{=}\frac{8}{5}\text{+}\frac{9}{20}\text{.}\frac{2}{5}$

   $=\frac{8}{5}\text{+}\frac{18}{100}\text{=}\frac{80}{50}\text{+}\frac{9}{50}\text{=}\frac{89}{50}.$

   Câu 4. Tính chất của phép nhân các số hữu tỉ bao gồm:

   A. Giao hoán, nhân với số 1;

   B. Kết hợp, phân phối của phép nhân đối với phép cộng và phép trừ;

   C. Cả đáp án A và B đều đúng;

   D. Không có đáp án nào đúng.

   Hướng dẫn giải

   Đáp án đúng là: C

   Phép nhân các số hữu tỉ cũng có các tính chất như phép nhân các số nguyên đó là: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân đối với phép cộng và phép trừ.

   Câu 5. Cho hai biểu thức sau, khẳng định nào sau đây đúng?

   $A\text{=}\frac{11}{2}\text{. 0,62 :}\left(\frac{-\text{3}}{100}\right);$ $B\text{=}\frac{12}{-\text{5}}\text{:}\frac{8}{45}\text{.}\frac{9}{10}.$

   A. A > B;

   B. A = B;

   C. A < B;

   D. A ≥ B.

   Hướng dẫn giải

   Đáp án đúng là: C.

   Ta có: $A\text{=}\frac{11}{2}\text{. 0,62 :}\left(\frac{-\text{3}}{100}\right)$

   $=\frac{11}{2}\text{.}\frac{62}{100}\text{.}\left(\frac{\text{100}}{-3}\right)$

   $=\frac{11}{2}\text{.}\frac{31}{50}\text{.}\left(\frac{-100}{3}\right)$

   $=\frac{341}{100}\text{.}\left(\frac{-\text{100}}{3}\right)\text{=}\frac{-\text{341}}{3};$

   $B\text{=}\frac{12}{-\text{5}}\text{:}\frac{8}{45}\text{.}\frac{9}{10}$

   $=\frac{12}{-\text{5}}\text{.}\frac{45}{8}\text{.}\frac{9}{10}$

   $=\frac{3}{\text{1}}\text{.}\frac{-9}{2}\text{.}\frac{9}{10}$

   $=\frac{-\text{27}}{2}\text{.}\frac{9}{10}\text{=}\frac{-\text{243}}{20}.$

   Mà $\frac{-\text{341}}{3}\text{<}\frac{-\text{300}}{3}\text{=}-\text{100;}$

   $-\text{100 =}\frac{-\text{2000}}{20}\text{<}\frac{-\text{243}}{20}.$

   Suy ra $\frac{-\text{341}}{3}\text{<}\frac{-\text{243}}{20}.$

   Vậychọn đáp án C.

   Câu 6. Kết quả của phép tính $0,5\text{+}\left(-\frac{3}{7}\right)$ là:

   A.$-\frac{1}{14};$

   B.$\frac{2}{7};$

   C.$\frac{1}{14};$

   D.$\frac{1}{10}.$

   Hướng dẫn giải

   Đáp án đúng là: C

   Ta có:$0,5\text{=}\frac{5}{10}\text{=}\frac{1}{2}.$

   Do đó: $0,5\text{+}\left(-\frac{3}{7}\right)\text{=}\frac{1}{2}\text{+}\left(-\frac{3}{7}\right)$

   $=\frac{1.7}{2.7}\text{+}\frac{\left(-\text{3}\right).2}{7.2}$

   $=\frac{7}{14}\text{+}\frac{-\text{6}}{14}$

   $=\frac{1}{14}.$

   Câu 7. Cho biết $\text{x +}\frac{2}{15}\text{=}-\frac{3}{10}$ thì:

   A.$\text{x =}\frac{-\text{13}}{30};$

   B.$\text{x =}\frac{11}{30};$

   C.$\text{x =}\frac{-5}{150};$

   D.$\text{x =}\frac{65}{150}.$

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: $x\text{+}\frac{2}{15}\text{=}-\frac{3}{10}$

   $x\text{=}-\frac{3}{10}-\frac{2}{15}$

   $x\text{=}\frac{-\text{9}}{30}-\frac{4}{30}$

   $x\text{=}\frac{-\text{9}-\text{4}}{30}$

   $x\text{=}\frac{-\text{13}}{30}.$

   Vậy $\text{x =}\frac{-\text{13}}{30}.$

   Câu 8. Số $\frac{-\text{5}}{18}$ là hiệu của hai số hữu tỉ nào dưới đây?

   A. $\frac{3}{18}-\frac{2}{18};$

   B. $\frac{1}{18}-\frac{2}{9};$

   C. $-\frac{1}{9}-\frac{1}{6};$

   D. $\frac{2}{9}-\frac{1}{3}.$

   Hướng dẫn giải

   Đáp án đúng là: C

   Ta có:$\frac{3}{18}-\frac{\text{2}}{18}\text{=}\frac{3-\text{2}}{18}\text{=}\frac{1}{18};$

   $\frac{1}{18}-\frac{2}{9}\text{=}\frac{1}{18}-\frac{4}{18}\text{=}\frac{-\text{3}}{18};$

   $-\frac{1}{9}-\frac{1}{6}\text{=}\frac{-\text{2}}{18}-\frac{3}{18}\text{=}\frac{-\text{5}}{18};$

   $\frac{2}{9}-\frac{1}{3}\text{=}\frac{2}{9}-\frac{3}{9}\text{=}\frac{-\text{1}}{9}.$

   Vậy chọn đáp án C.

   Câu 9. Kết luận nào đúng về giá trị của biểu thức $\text{A =}\frac{1}{5}-\left(\left(\frac{-\text{2}}{3}\right)-\left(\frac{1}{3}\text{+}\frac{5}{6}\right)\right)?$

   A. A < 2

   B. A > 2

   C. A < 1

   D. A < 0

   Hướng dẫn giải

   Đáp án đúng là: B

   Ta có: $A\text{=}\frac{1}{5}-\left(\left(\frac{-\text{2}}{3}\right)-\left(\frac{1}{3}\text{+}\frac{5}{6}\right)\right)$

   $=\frac{1}{5}-\left(\left(\frac{-\text{2}}{3}\right)-\left(\frac{2}{6}\text{+}\frac{5}{6}\right)\right)$

   $=\frac{1}{5}-\left(\frac{-\text{2}}{3}-\frac{7}{6}\right)$

   $=\frac{1}{5}-\left(\frac{-\text{4}}{6}-\frac{7}{6}\right)$

   $=\frac{1}{5}-\frac{-\text{11}}{6}$

   $=\frac{6}{30}-\frac{-\text{55}}{30}$

   $=\frac{6-\left(-\text{55}\right)}{30}$

   $=\frac{61}{30}.$

   Do $A=\frac{61}{30}>\frac{60}{30}=2$nên A > 2.

   Câu 10. Chọn khẳng định đúng về quy tắc chuyển vế đối với số hữu tỉ:

   A. Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức thì ta giữ nguyên dấu của số hạng đó;

   B. Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức thì ta đổi dấu số hạng còn lại;

   C. Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức thì ta đổi dấu của tất cả các số hạng trong phép tính;

   D. Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức thì ta phải đổi dấu số hạng đó.

   Hướng dẫn giải

   Đáp án đúng là: D

   Quy tắc chuyển vế đối với số hữu tỉ tương tự đối với số nguyên: khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó.

   Câu 11. Tìm x, biết:

   A. x = 0;

   B. x = 1;

   C. x = ‒1;

   D. x = 2.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có:$\left(x-\frac{4}{5}\right)\text{:}\frac{1}{2}\text{=}\frac{-8}{5}$

   $\text{x}-\frac{4}{5}\text{=}\frac{-8}{5}\text{.}\frac{1}{2}$

   $\text{x}-\frac{4}{5}\text{=}\frac{-\text{4}}{5}$

   $\text{x =}\frac{-\text{4}}{5}\text{+}\frac{4}{5}$

   $\text{x =}\frac{-\text{4 + 4}}{5}$

   $x=\frac{0}{5}$

   x = 0

   Vậy x = 0.

   Câu 12. Số nghịch đảo của số − 0,8 là:

   A. 0,8;

   B.$\frac{-\text{8}}{10};$

   C.$\frac{5}{4};$

   D.$\frac{-\text{5}}{4}.$

   Hướng dẫn giải

   Đáp án đúng là: D.

   Do số nghịch đảo của số hữu tỉ a khác 0 là $\frac{1}{\text{a}}$ nên số nghịch đảo của − 0,8 là:

   $\frac{1}{-\text{0,8}}\text{=}\frac{-\text{10}}{8}\text{=}\frac{-\text{5}}{4}.$

   Câu 13. Một ô tô đi từ A đến B với vận tốc 50,5 km/giờ mất 1 giờ 30 phút. Một chiếc xe máy đi với vận tốc bằng $\frac{5}{6}$ vận tốc của ô tô thì sau bao lâu sẽ đi hết quãng đường AB?

   A.$\frac{9}{5}$ giờ;

   B.$\frac{3}{2}$ giờ;

   C.$\frac{4}{3}$ giờ;

   D. 2 giờ.

   Hướng dẫn giải

   Đáp án đúng là: A.

   Đổi: 1 giờ 30 phút = 1$\frac{1}{2}$ giờ = $\frac{3}{2}$ giờ;

   Quãng đường AB dài số km là:

   $50,5\text{.}\frac{3}{2}\text{=}\frac{101}{2}\text{.}\frac{3}{2}\text{=}\frac{303}{4}$(km);

   Vận tốc của xe máy là:

   $50,5\text{.}\frac{5}{6}\text{=}\frac{101}{2}\text{.}\frac{5}{6}\text{=}\frac{505}{12}$(km/ giờ);

   Thời gian xe máy đi hết quãng đường AB là:

   $\frac{303}{4}\text{:}\frac{505}{12}\text{=}\frac{303}{4}\text{.}\frac{12}{505}\text{=}\frac{3.101}{4}\text{.}\frac{3.4}{5.101}\text{=}\frac{9}{5}$(giờ).

   Câu 14. Trong bộ số liệu chuẩn, trên thực tế diện tích bề mặt hồ Tây tại Hà Nội là 5,3 km². Minh thiết kế một bản vẽ có tỉ lệ $\frac{1}{150000}$ , xác định diện tích bề mặt của hồ là 0,000004 km². Số liệu của Minh chênh lệch như thế nào với số liệu chuẩn?

   A. Số liệu của Minh nhỏ hơn số liệu chuẩn;

   B. Số liệu của Minh lớn hơn số liệu chuẩn;

   C. Số liệu của Minh không chênh lệch so với số liệu chuẩn;

   D. Không xác định được.

   Hướng dẫn giải

   Đáp án đúng là: A

   Với số liệu của Minh thì thực tế diện tích bề mặt hồ là:

   $0,000004\text{. 150000 =}\frac{4}{1000000}\text{. 150000 =}\frac{4}{100}.15=\frac{60}{100}\text{= 0,6 km < 5,3 km.}$

   Vậy số liệu của Minh nhỏ hơn số liệu chuẩn.

   Câu 15. Cho các số hữu tỉ sau: $\frac{1}{2},\frac{-\text{3}}{4},\frac{-\text{5}}{6},\frac{2}{5}$ . Biểu thức được tạo thành từ các số hữu tỉ trên là:

   A.null

   B.$\frac{2}{5}\text{.}\left(\frac{1}{2}\text{+}\frac{-\text{3}}{4}\right)\text{=}\frac{-\text{5}}{6};$

   C.$\frac{-5}{6}\text{.}\frac{1}{2}-\frac{2}{5}\text{=}\frac{-\text{3}}{4};$

   D.$\frac{-\text{3}}{4}\text{:}\left(\frac{1}{2}\text{+}\frac{2}{5}\right)\text{=}\frac{-\text{5}}{6}.$

   Hướng dẫn giải

   Đáp án đúng là: D

   Ta có:

   +)$\frac{-\text{3}}{4}\text{.}\left(\frac{1}{2}\text{+}\frac{2}{5}\right)\text{=}\frac{-\text{3}}{4}\text{.}\left(\frac{5}{10}\text{+}\frac{4}{10}\right)$

   $=\frac{-\text{3}}{4}\text{.}\frac{9}{10}\text{=}\frac{-\text{27}}{40};$

   +)$\frac{2}{5}\text{.}\left(\frac{1}{2}\text{+}\frac{-\text{3}}{4}\right)\text{=}\frac{2}{5}\text{.}\left(\frac{4}{8}\text{+}\frac{-\text{6}}{8}\right)$

   $=\frac{2}{5}\text{.}\frac{-\text{2}}{8}\text{=}\frac{-\text{4}}{40}\text{=}\frac{-\text{1}}{10}\text{;}$

   +)$\frac{-5}{6}\text{.}\frac{1}{2}-\frac{2}{5}\text{=}\frac{-\text{5}}{12}-\frac{2}{5}$

   $=\frac{-\text{25}}{60}-\frac{24}{60}\text{=}\frac{-\text{49}}{60};$

   +)$\frac{-\text{3}}{4}\text{:}\left(\frac{1}{2}\text{+}\frac{2}{5}\right)\text{=}\frac{-\text{3}}{4}\text{:}\left(\frac{5}{10}\text{+}\frac{4}{10}\right)$

   $=\frac{-3}{4}\text{:}\frac{9}{10}\text{=}\frac{-\text{3}}{4}\text{.}\frac{10}{9}\text{=}\frac{-\text{30}}{36}\text{=}\frac{-\text{5}}{6}.$

   Vậy $\frac{-\text{3}}{4}\text{:}\left(\frac{1}{2}\text{+}\frac{2}{5}\right)\text{=}\frac{-\text{5}}{6}.$

   Xem thêm các bài trắc nghiệm Toán 7 Cánh diều hay, chi tiết khác:

   Trắc nghiệm Toán 7 Bài 1: Tập hợp Q các số hữu tỉ

   Trắc nghiệm Toán 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

   Trắc nghiệm Toán 7 Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

   Trắc nghiệm Toán 7 Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc

   Trắc nghiệm Toán 7 Bài 5: Biểu diễn thập phân của số hữu tỉ
5. Vở bài tập Toán 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ – Cánh diều
   Giải VBT Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

   I. Kiến thức trọng tâm

   Câu 1 trang 8 vở bài tập Toán lớp 7 Tập 1: Phép cộng các số hữu tỉ có các tính chất: …………………………………….

   Trong một biểu thức số chỉ gồm các phép cộng và phép trừ, ta có thể thay đổi tùy ý vị trí các số hạng kèm theo ………………………..

   Lời giải:

   Phép cộng các số hữu tỉ có các tính chất: giao hoán, kết hợp, cộng với số 0, cộng với số đối.

   Trong một biểu thức số chỉ gồm các phép cộng và phép trừ, ta có thể thay đổi tùy ý vị trí các số hạng kèm theo dấu của chúng.

   Câu 2 trang 9 vở bài tập Toán lớp 7 Tập 1: Khi di chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải ……………………………………………

   Lời giải:

   Khi di chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu của số hạng đó: dấu cộng thành dấu trừ và dấu trừ thành dấu cộng.

   Câu 3 trang 9 vở bài tập Toán lớp 7 Tập 1: Phép nhân các số hữu tỉ có các tính chất: ……………………………….

   Lời giải:

   Phép nhân các số hữu tỉ có các tính chất: giao hoán; kết hợp; nhân với 1; phân phối của phép nhân đối với phép cộng và phép trừ.

   II. Luyện tập

   • Câu 1 trang 9 vở bài tập Toán lớp 7 Tập 1: Tính:

     a) $\frac{5}{7}-(-3,9)=$ …………………

     b) (–3,25) + $4\frac{3}{4}$ = …………….

     Lời giải:

     a) $\frac{5}{7}-(-3,9)=\frac{5}{7}+\frac{39}{10}=\frac{5.10}{7.10}+\frac{39.7}{10.7}=\frac{50}{70}+\frac{273}{70}=\frac{323}{70}$.

     b) $(-3,25)+4\frac{3}{4}=\frac{-325}{100}+\frac{19}{4}=\frac{\left(-325\right):25}{100:25}+\frac{19}{4}=\frac{-13}{4}+\frac{19}{4}=\frac{6}{4}=\frac{3}{2}$.

   • Câu 2 trang 9 vở bài tập Toán lớp 7 Tập 1: Tính một cách hợp lí:

     a) $(-0,4)+\frac{3}{8}+(-0,6)$ = …………………………………………………..

     b) $\frac{4}{5}-1,8+0,375+\frac{5}{8}$ = ………………………………………………….

     Lời giải:

     a) $(-0,4)+\frac{3}{8}+(-0,6)$ = $(-0,4)+(-0,6)+\frac{3}{8}$$$

     =[(− 0,4)+(− 0,6)]+38= −1 + $\frac{3}{8}$ = $\frac{-5}{8}$.

     b) $\frac{4}{5}-1,8+0,375+\frac{5}{8}$

     = 0,8 – 1,8 + 0,375 + 0,625 = (0,8 – 1,8) + (0,375 + 0,625) = (– 1) + 1 = 0.

   • Câu 3 trang 9 vở bài tập Toán lớp 7 Tập 1: Tính

     a) $x-\left(-\frac{7}{9}\right)=-\frac{5}{6}$;

     b) $\frac{15}{-4}-x=0,3.$

     Lời giải:

     a) $x-\left(-\frac{7}{9}\right)=-\frac{5}{6}$

     .$x=\left(-\frac{5}{6}\right)+\left(-\frac{7}{9}\right)$

     .$x=-\left(\frac{5}{6}+\frac{7}{9}\right)$

     .$x=-\left(\frac{5.3}{6.3}+\frac{7.2}{9.2}\right)$

     .$x=-\left(\frac{15}{18}+\frac{14}{18}\right)$

     .$x=-\frac{29}{18}$

     Vậy $x=-\frac{29}{18}$.

     b) $\frac{15}{-4}-x=0,3.$

     $\frac{15}{-4}-x=\frac{3}{10}$

     .$x=-\frac{15}{4}-\frac{3}{10}$

     .$x=\frac{\left(-15\right).5}{4.5}-\frac{3.2}{10.2}$

     .$x=\frac{-75}{20}-\frac{6}{20}$

     .$x=-\left(\frac{75}{20}+\frac{6}{20}\right)$

     .$x=-\frac{81}{20}$

     Vậy $x=-\frac{81}{20}$.

   • Câu 4 trang 10 vở bài tập Toán lớp 7 Tập 1: Đèo Hải Vân là một cung đường hiểm trở trên tuyến giao thông xuyên suốt Việt Nam. Để thuận lợi cho việc đi lại, người ta đã xây dựng hầm đường bộ xuyên đèo Hải Vân. Hầm Hải Vân có chiều dài là 6,28 km và bằng $\frac{157}{500}$ độ dài của đèo Hải Vân.

     (Nguồn: http://ww.songda.vn)

     Độ dài của đèo Hải Vân là bao nhiêu ki–lô–mét?

     Lời giải:

     Độ dài của đèo Hải Vân là:

     $6,28:\frac{157}{500}=\frac{628}{100}:\frac{157}{500}=\frac{157}{25}.\frac{500}{157}=\frac{500}{25}=20$(km).

   • Câu 5 trang 10 vở bài tập Toán lớp 7 Tập 1: Một ô tô đi từ tỉnh A đến tỉnh B. Trong 1 giờ đầu, ô tô đã đi được $\frac{2}{5}$ quãng đường. Hỏi với vận tốc đó, ô tô phải mất bao lâu để đi hết cả quãng đường AB?

     Lời giải:

     Thời gian ô tô đi hết quãng đường AB là:

     $1:\frac{2}{5}=\frac{5}{2}=2,5$ (giờ)

     Vậy với vận tốc đó, ô tô phải mất 2,5 giờ để đi hết cả quãng đường AB.

   • Câu 6 trang 10 vở bài tập Toán lớp 7 Tập 1: Tính một cách hợp lí:

     a) $\frac{7}{3}.\left(-2,5\right).\frac{6}{7}$ = ……………………………..

     b) $0,8.\frac{-2}{9}-\frac{4}{5}.\frac{7}{9}-0,2$ = ……………………….

     Lời giải:

     a) $\frac{7}{3}.(-2,5).\frac{6}{7}\text{=}\frac{7}{3}.\frac{6}{7}.(-2,5)=\frac{6}{3}.\frac{-5}{2}=\frac{6.\left(-5\right)}{3.2}=\frac{-30}{6}=-5$.

     b) $0,8.\frac{-2}{9}-\frac{4}{5}.\frac{7}{9}-0,2=\frac{4}{5}.\frac{-2}{9}-\frac{4}{5}.\frac{7}{9}-0,2$

     $=\frac{4}{5}.\left(\frac{-2}{9}-\frac{7}{9}\right)-0,2=\frac{4}{5}.\left(\frac{\left(-2\right)-7}{9}\right)-0,2=\frac{4}{5}.(-1)-\frac{1}{5}$

   • $=\frac{\left(-4\right)-1}{5}=\frac{-5}{5}=-1$

   • Câu 7 trang 10 vở bài tập Toán lớp 7 Tập 1:

     a) Số nghịch đảo của số $2\frac{1}{5}$ ………………………………………….

     b) Số nghịch đảo của số –13 là ………………………………………

     Lời giải:

     a) Số nghịch đảo của số $2\frac{1}{5}$ là $\frac{5}{11}$. (Do $2\frac{1}{5}=\frac{11}{5}$).

     b) Số nghịch đảo của số –13 là $\frac{-1}{13}$.

   • III. Bài tập

     • Câu 1 trang 10 vở bài tập Toán lớp 7 Tập 1: Tính:

       a) $\frac{-1}{6}+0,75=$ ……………………………………………………….

       b) $3\frac{1}{10}-\frac{3}{8}=$ …………………………………………………………

       c) $0,1+\frac{-9}{17}-\left(-0,9\right)=$ ……………………………………………….

       Lời giải:

       a) $\frac{-1}{6}+0,75=\frac{-1}{6}+\frac{3}{4}=\frac{\left(-1\right).2}{6.2}+\frac{3.3}{3.4}=\frac{-2}{12}+\frac{9}{12}=\frac{7}{12}$;

       b) $3\frac{1}{10}-\frac{3}{8}=\frac{31}{10}-\frac{3}{8}=\frac{31.4}{10.4}-\frac{3.5}{8.5}=\frac{124}{40}-\frac{15}{40}=\frac{109}{40}$;

       c) $0,1+\frac{-9}{17}-(-0,9)=0,1+\frac{-9}{17}+0,9=\left(0,1+0,9\right)+\frac{-9}{17}=1+\frac{-9}{17}$

       $=\frac{17}{17}+\frac{-9}{17}=\frac{8}{17}$.

     • Câu 2 trang 11 vở bài tập Toán lớp 7 Tập 1: Tính:

       a) $5,75.\frac{-8}{9}$= ………………………………………………

       b) $2\frac{3}{8}.(-0,4)$ = ……………………………………………

       c) $\frac{-12}{5}:(-6,5)$ = …………………………………………….

       Lời giải:

       a) $5,75.\frac{-8}{9}=\frac{575}{100}.\frac{-8}{9}=\frac{23}{4}.\frac{-8}{9}=\frac{\mathrm{23.4.}\left(-2\right)}{4.9}=\frac{-46}{9}$.

       b) $2\frac{3}{8}.(-0,4)=\frac{19}{8}.\frac{-4}{10}=\frac{19.\left(-4\right)}{\left(-4\right).\left(-2\right).10}=\frac{-19}{20}$.

       c) $\frac{-12}{5}:(-6,5)=\frac{-12}{5}:\frac{-65}{10}=\frac{12}{5}:\frac{65}{10}=\frac{12}{5}:\frac{13}{2}=\frac{12}{5}.\frac{2}{13}=\frac{24}{65}$.

     • Câu 3 trang 11 vở bài tập Toán lớp 7 Tập 1: Tính một cách hợp lí:

       a) $\frac{-3}{10}-0,125+\frac{-7}{10}+1,125$ = ……………………………………………

       b) $\frac{-8}{3}.\frac{2}{11}-\frac{8}{3}:\frac{11}{9}$= ………………………………………………………

       Lời giải:

       a) $\frac{-3}{10}-0,125+\frac{-7}{10}+1,125=\frac{-3}{10}+\frac{-7}{10}+1,125-0,125$

       $=-\left(\frac{3}{10}+\frac{7}{10}\right)+(1,125-0,125)$

       $=-\frac{10}{10}+1$ = − 1 + 1 = 0.

       b) $\frac{-8}{3}.\frac{2}{11}-\frac{8}{3}:\frac{11}{9}=-\frac{8}{3}.\frac{2}{11}-\frac{8}{3}.\frac{9}{11}=-\frac{8}{3}.\left(\frac{2}{11}+\frac{9}{11}\right)=-\frac{8}{3}.1=-\frac{8}{3}$.

     • Câu 4 trang 11 vở bài tập Toán lớp 7 Tập 1: Tìm x, biết:

       a) $x+\left(-\frac{1}{5}\right)=\frac{-4}{15}$

       ……………….

       b) $3,7-x=\frac{7}{10}$

       …………………

       c) $x.\frac{3}{2}=2,4$

       ………………

       d) $3,2:x=-\frac{6}{11}$

       ………………..

       Lời giải:

       a)

       $x+\left(-\frac{1}{5}\right)=\frac{-4}{15}$

       $x=\frac{-4}{15}-\left(-\frac{1}{5}\right)$

       $x=\frac{-4}{15}+\frac{1}{5}$

       $x=\frac{-4}{15}+\frac{3}{15}$

       $x=\frac{-1}{15}$

       Vậy $x=\frac{-1}{15}$.

       b) $3,7-x=\frac{7}{10}$

       $\frac{37}{10}$ – x = $\frac{7}{10}$

       x = $\frac{37}{10}$ – $\frac{7}{10}$

       x = $\frac{30}{10}$

       x = 3

       Vậy x = 3.

       c) $x.\frac{3}{2}=2,4$

       x.$\frac{3}{2}$= $\frac{24}{10}$

       x = $\frac{24}{10}:\frac{3}{2}$

       $x=\frac{24}{10}.\frac{2}{3}$

       $x=\frac{8}{5}$

       Vậy $x=\frac{8}{5}$.

       d) $3,2:x=-\frac{6}{11}$

       $\frac{32}{10}:x=-\frac{6}{11}$

       $x=\frac{32}{10}:\left(-\frac{6}{11}\right)$

       $x=\frac{32}{10}.\left(-\frac{11}{6}\right)$

       $x=-\frac{88}{15}$

       Vậy $x=-\frac{88}{15}$.

     • Câu 5 trang 12 vở bài tập Toán lớp 7 Tập 1: Bác Nhi gửi vào ngân hàng 60 triệu đồng với kì hạn 1 năm, lãi suất 6,5%/năm. Hết kì hạn 1 năm, bác rút ra $\frac{1}{3}$ số tiền (kể cả gốc và lãi). Tính số tiền còn lại của bác Nhi trong ngân hàng.

       Lời giải:

       Số tiền bác Nhi có được sau khi hết kì hạn 1 năm là:

       60 + 60 . 6,5% = 60 + 3,9 = 63,9 (triệu đồng)

       Số tiền bác Nhi rút ra là:

       63,9.$\frac{1}{3}$ = 21,3 (triệu đồng)

       Số tiền còn lại của bác Nhi trong ngân hàng là:

       63,9 – 21,3 = 42,6 (triệu đồng) = 42 600 000 (đồng).

     • Câu 6 trang 12 vở bài tập Toán lớp 7 Tập 1: Tính diện tích mặt bằng của ngôi nhà được mô tả như Hình 2 (các số đo trên hình tính theo đơn vị mét).

       

       Lời giải:

       Diện tích phòng ngủ là:

       5,1 . 4,7 = 23,97 (m²)

       Diện tích phòng bếp là:

       7,1 . 3,4 = 24,14 (m²)

       Chiều dài phòng khách là:

       2,0 + 4,7 = 6,7 (m)

       Diện tích phòng khách là:

       6,7 . 5,8 = 38,86 (m²)

       Chiều dài hai phòng vệ sinh là:

       2,6 + 2,5 = 5,1 (m)

       Diện tích hai phòng vệ sinh là:

       5,1 . 2,0 = 10,2 (m²)

       Diện tích mặt bằng của ngôi nhà là:

       23,97 + 24,14 + 38,86 + 10,2 = 97,17 (m²)

       Vậy diện tích mặt bằng của ngôi nhà trong hình vẽ là 97,17 m².

     • Câu 7 trang 12 vở bài tập Toán lớp 7 Tập 1: Theo yêu cầu của kiến trúc sư, ổ cắm điện và vòi nước của nhà chú Năm cách nhau tối thiểu là 60 cm. Trên bản vẽ có tỉ lệ 1 : 20 của thiết kế nhà chú Năm, khoảng cách từ ổ cắm điện đến vòi nước đo được là 2,5 cm. Khoảng cách trên bản vẽ như vậy có phù hợp với yêu cầu của kiến trúc sư không? Giải thích vì sao.

       Lời giải:

       Trên bản vẽ có tỉ lệ 1 : 20 của thiết kế nhà chú Năm, khoảng cách từ ổ cắm điện đến vòi nước đo được là 2,5 cm thì trên thực tế khoảng cách đó sẽ là:

       $2,5:\frac{1}{20}=\frac{5}{2}:\frac{1}{20}=\frac{5}{2}.20=50$ (cm) .

       Theo yêu cầu của kiến trúc sư, khoảng cách tối thiểu giữa ổ cắm và vòi nước của nhà chú Năm là 60 cm (tức là khoảng cách từ ổ cắm và vòi nước phải lớn hơn hoặc bằng 60cm).

       Vì 50 < 60 nên khoảng cách trên bản vẽ không phù hợp với yêu cầu của kiến trúc sư.

     • Câu 8 trang 13 vở bài tập Toán lớp 7 Tập 1: Inch (kí hiệu là in) là tên của một đơn vị đo độ dài: 1 in = 2,54 cm. Đường kính bánh xe đạp của bạn Vinh là 26 in. Khi đi được 1 km thì mỗi bánh xe đạp của bạn Vinh quay được khoảng bao nhiêu vòng? (Làm tròn kết quả đến hàng đơn vị; lấy π ≈ 3,14).

       Lời giải:

       Đường kính bánh xe đạp của bạn Vinh ở đơn vị cm là:

       26 . 2,54 = 66,04 (cm)

       Chu vi bánh xe đạp của bạn Vinh là:

       66,04 . 3,14 = 207,3656 (cm)

       Đổi 1 km = 100 000 cm

       Số vòng bánh xe bạn Vinh quay được khi đi được 1 km là:

       100 000 : 207,3656 ≈ 482 (vòng).

     • Câu 9 trang 13 vở bài tập Toán lớp 7 Tập 1: Biểu đồ cột ở Hình 3 thống kê kim ngạch nhập khẩu hàng hóa (tức là số tiền chi ra để nhập khẩu hàng hóa) của Việt Nam trong các năm 2016, 2017, 2018, 2019, 2020.

       

       a) Kim ngạch nhập khẩu hàng hóa năm 2019 của Việt Nam tăng bao nhiêu phần trăm so với năm 2018? (Làm tròn kết quả đến hàng phần mười).

       b) Kim ngạch nhập khẩu hàng hóa năm 2020 tăng bao nhiêu phần trăm so với năm 2019? (Làm tròn kết quả đến hàng phần mười).

       Lời giải:

       a) Kim ngạch nhập khẩu hàng hóa năm 2019 của Việt Nam tăng số tiền so với năm 2018 là:

       253,07 – 236,7 = 16,37 (tỉ đô la Mỹ).

       Kim ngạch nhập khẩu hàng hóa năm 2019 của Việt Nam tăng số phần trăm so với năm 2018 là:

       16,37 : 236,7 . 100% ≈ 6,9%.

       b) Kim ngạch nhập khẩu hàng hóa năm 2020 của Việt Nam tăng số tiền so với năm 2019 là:

       262,4 – 253,07 = 9,33 (tỉ đô la Mỹ).

       Kim ngạch nhập khẩu hàng hóa năm 2020 của Việt Nam tăng số phần trăm so với năm 2019 là:

       9,33 : 253,07 . 100% ≈ 3,7%.