Câu hỏi:
Gọi M, N theo thứ tự là các trung điểm của hai đáy AD và BC của hình thang ABCD. Từ điểm O tùy ý thuộc đoạn MN, kẻ đường thẳng song song với đáy hình thang, đường thẳng này cắt các cạnh bên tại E và F. Chứng minh rằng O là trung điểm của EF.
Trả lời:
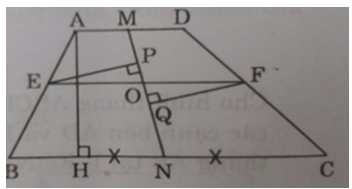 Ta có MA = MD, NC = NB (gt) và AD // BC.
Ta có MA = MD, NC = NB (gt) và AD // BC.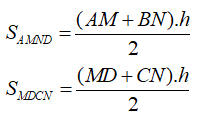 ⇒ SAMND = SMCDN (các hình thang có các đáy bằng nhau và chung đường cao)Do EF // AD nên đường cao từ E và F xuống AD bằng nhau, lại có AM = DM⇒ SAEM = SDFMTương tự SBEN = SNFC⇒ SAMNB – (SAEM + SBEN) = SDMNC – (SBEN + SNFC)hay SEMN = SFMNHai tam giác trên có chung cạnh MN nên đường cao tương ứng bằng nhau hay EP = FQXét ΔEPO và ΔFQO có:∠EOP = ∠QOF (đối đỉnh)EP = PQ (cmt)∠EPO = ∠FQO = 90oDo đó ΔEPO = ΔFQO (ch–gn) ⇒ OE = OF hay O là trung điểm của EF.
⇒ SAMND = SMCDN (các hình thang có các đáy bằng nhau và chung đường cao)Do EF // AD nên đường cao từ E và F xuống AD bằng nhau, lại có AM = DM⇒ SAEM = SDFMTương tự SBEN = SNFC⇒ SAMNB – (SAEM + SBEN) = SDMNC – (SBEN + SNFC)hay SEMN = SFMNHai tam giác trên có chung cạnh MN nên đường cao tương ứng bằng nhau hay EP = FQXét ΔEPO và ΔFQO có:∠EOP = ∠QOF (đối đỉnh)EP = PQ (cmt)∠EPO = ∠FQO = 90oDo đó ΔEPO = ΔFQO (ch–gn) ⇒ OE = OF hay O là trung điểm của EF.
====== **** mời các bạn xem câu tiếp bên dưới **** =====