Câu hỏi:
(3 điểm): Cho tam giác ABC, các điểm M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Trên tia đối của tia NP lấy điểm D sao cho ND = NP.a) Chứng minh: Tứ giác ADCP là hình bình hành.b) Gọi F là giao điểm của MN và DC. Giả sử MN = 3cm. Tính BC và chứng minh FD = FC.c) Gọi H là giao điểm của AP và MN; I là giao điểm của NP và HC. Chứng minh: B, I, F thẳng hàng.
Trả lời:
Hướng dẫn giải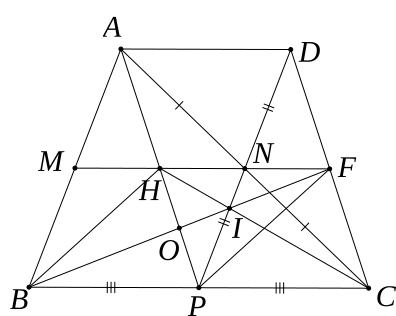
a) Xét tứ giác ADCP có:N là trung điểm của ACN là trung điểm của DP (ND = NP)⇒ tứ giác ADCP là hình bình hành.b) Xét tam giác ABC có:M là trung điểm ABN là trung điểm AC⇒ MN là đường trung bình tam giác ABC⇒ MN//BC, \(MN = \frac{1}{2}BC\)⇒ BC = 2MN = 2.3 = 6cmTa có MN//BC (MN là đường trung bình tam giác ABC)⇒ NF//PCTrong tam giác DCP có:N là trung điểm của DPNF//PC⇒ F là trung điểm của DCHay DF = FCSuy ra NF là đường trung bình của ΔDCP.\( \Rightarrow NF = \frac{1}{2}PC\)c) Chứng minh tương tự: HN là đường trung bình của ΔACP và H là trung điểm của AP\( \Rightarrow HN = \frac{1}{2}PC\)Ta có: \(HF = HN + NF = \frac{1}{2}PC + \frac{1}{2}PC = PC\)Mà có: PC = PB nên HN= PBXét tứ giác BHFP có HN = PB và HN // PB (vì MN//BC)⇒ BHFP là hình hình hànhGọi BF cắt HP tại O. Khi đó O là trung điểm của BF và HP.Trong tam giác APC có CH và PN là đường trung tuyếnvà CH cắt PN tại II là trọng tâm tam giác APC\( \Rightarrow PI = \frac{2}{3}PN\)Trong tam giác PHF có: PN là đường trung tuyến và \(PI = \frac{2}{3}PN\)I là trọng tâm tam giác PHFmà có FO là đường trung tuyến (vì O là trung điểm của HP)I thuộc FOF, I, O thẳng hàngmà F, O, B thẳng hàngnên B, I, F thẳng hàng.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Kết quả phép tính –3a(2a2– 5b) bằng:
Câu hỏi:
Kết quả phép tính –3a(2a2– 5b) bằng:
A. 6a3– 15ab;
B. 6a3– 3a;
C. –6a3– 15ab;
D. –6a3+ 15ab.
Đáp án chính xác
Trả lời:
Đáp án đúng là: DTa có: –3a . (2a2– 5b) = –6a3+ 15ab.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Giá trị của biểu thức x2– 4x + 4 tại x = 2 là:
Câu hỏi:
Giá trị của biểu thức x2– 4x + 4 tại x = 2 là:
A. 2;
B. 0;
Đáp án chính xác
C. 16;
D. 4.
Trả lời:
Đáp án đúng là: BTại x = 2 thì: x2– 4x + 4 = 22– 4.2 + 4 = 0.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các cách viết sau, cách viết nào đúng?
Câu hỏi:
Trong các cách viết sau, cách viết nào đúng?
A. (x – y)(y + x) = y2– x2;
B. x2– 2x + 1 = (x + 1)2;
C. (x – 2)2= x2– 2x + 4;
D. (2x – 1)(4x2+ 2x + 1) = 8x3– 1.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D(x – y)(y + x) = xy + x2– y2– xy = x2– y2→ Đáp án A Saix2– 2x + 1 = (x – 1)2 → Đáp án B Sai(x – 2)2= x2– 4x + 4 → Đáp án C Sai(2x – 1)(4x2+ 2x + 1) = 8x3+ 4x2+ 2x – 4x2– 2x – 1 = 8x3– 1 → Đáp án D Đúng
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tìm x, biết x2– 25 = 0, ta được:
Câu hỏi:
Tìm x, biết x2– 25 = 0, ta được:
A. x = 5;
B. x = 5, x = – 5;
Đáp án chính xác
C. x = – 5;
D. x = 25.
Trả lời:
Đáp án đúng là: Bx2– 25 = 0⇔ (x + 5)(x – 5) = 0\( \Leftrightarrow \left[ \begin{array}{l}x + 5 = 0\\x – 5 = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = – 5\\x = 5\end{array} \right.\)Vậy x = 5, x = – 5.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Phân tích đa thức: 5×2– 10x thành nhân tử ta được kết quả nào đây?
Câu hỏi:
Phân tích đa thức: 5x2– 10x thành nhân tử ta được kết quả nào đây?
A. 5x(x – 10);
B. 5x(x2– 2x);
C. 5x(x – 2);
Đáp án chính xác
D. 5x(2 – x).
Trả lời:
Đáp án đúng là: CTa có: 5x2– 10x = 5x(x – 2).
====== **** mời các bạn xem câu tiếp bên dưới **** =====