Cho ngôi nhà có kích thước như hình vẽ. Tính diện tích xung quanh của ngôi nhà? Biết mái nhà là hình lăng trụ tam giác có đáy là hình tam giác đều.

Câu hỏi:

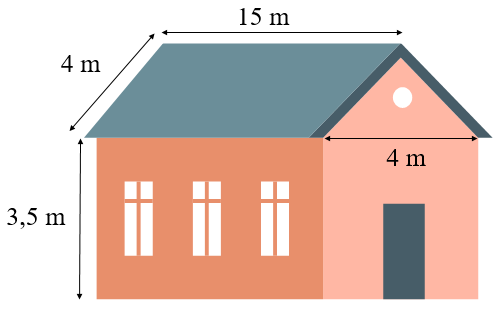
Cho ngôi nhà có kích thước như hình vẽ. Tính diện tích xung quanh của ngôi nhà? Biết mái nhà là hình lăng trụ tam giác có đáy là hình tam giác đều.

A. 253 m³;

Đáp án chính xác

B. 123 m²;

C. 313 m²;

D. 543 m³.

Trả lời:

Đáp án đúng là: A
Chia ngôi nhà ra làm hai phần là phần mái nhà và phần khung nhà để tính.
Diện tích xung quanh phần mái nhà là:
S_{xq mái} = (4 + 4 + 4).15 = 180 (m²)
Diện tích xung quanh phần khung nhà là:
S_{xq khung} = 2.(4 + 15).3,5 = 133 (m²)
Diện tích trần nhà là: 15 . 4 = 60 (m²)
Do khi tính diện tích mái nhà và diện tích khung nhà thì diện tích trần nhà được tính hai lần. Do đó diện tích xung quanh của cả ngôi nhà là:
180 + 133 – 60 = 253 (m²)
^{Vậy diện tích xung quanh của ngôi nhà bằng} 253 (m²).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình vẽ. Tính góc FEC, biết EF // DC và \[\widehat {ECB} = 60^\circ \]:
   
   

   Câu hỏi:
   

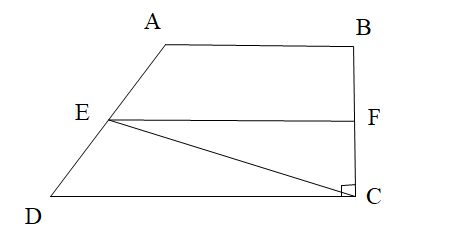
   Cho hình vẽ. Tính góc FEC, biết EF // DC và \[\widehat {ECB} = 60^\circ \]:
   

   A. 50°;

   B. 40°;

   C. 60°;

   D. 30°.

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   Vì EF // DC nên ta có: \[\widehat {ECD} = \widehat {F{\rm{E}}C}\] (hai góc so le trong)
   Ta có \[\widehat {BCD} = 90^\circ \] hay \[\widehat {FCE} + \widehat {ECD} = 90^\circ \] suy ra \[\widehat {ECD} = 90^\circ – 60^\circ = 30^\circ \].
   Do đó \[\widehat {FEC} = \widehat {ECD} = 30^\circ \].
   Vậy chọn đáp án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình bình hành ABCD như hình vẽ. Chọn phương án đúng.
   
   

   Câu hỏi:
   

   Cho hình bình hành ABCD như hình vẽ.
   
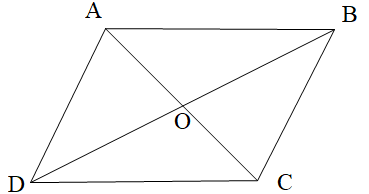
   Chọn phương án đúng.

   A. \[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù;

   B. \[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc so le trong;

   C. \[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc đồng vị;

   D. \[\widehat {AOB}\] và \[\widehat {DOC}\] là hai góc đối đỉnh.

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   \[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù là phát biểu sai vì hai góc này không chung đỉnh.
   \[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc so le trong là phát biểu sai, vì \[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc kề bù;
   \[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc trong cùng phía.
   \[\widehat {AOB}\] và \[\widehat {DOC}\] là hai góc đối đỉnh là phát biểu đúng, chọn phương án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hình bình hành ABCD như hình vẽ. Biết IJ // DC và \[\widehat {JOC} = 34^\circ \]. Số đo góc OCD là:
   
   

   Câu hỏi:
   

   Cho hình bình hành ABCD như hình vẽ. Biết IJ // DC và \[\widehat {JOC} = 34^\circ \].
   
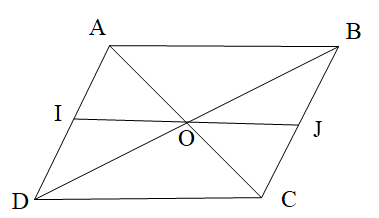
   Số đo góc OCD là:

   A. 60°;

   B. 34°;

   Đáp án chính xác

   C. 40°;

   D. 84°.

   Trả lời:

   Đáp án đúng là: B.
   Vì DC // IJ nên ta có: \[\widehat {JOC} = \widehat {OCD}\] (hai góc so le trong).
   Do đó \[\widehat {OCD} = \widehat {JOC} = 34^\circ \].
   Vậy chọn đáp án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
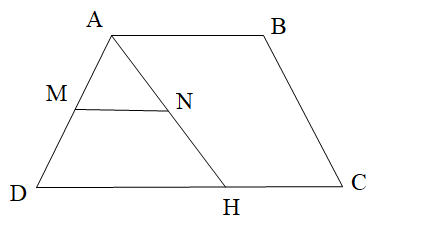
4. Cho hình thang ABCD như hình vẽ. Biết MN // DC, \[\widehat {DAB} = 120^\circ \] và \[\widehat {ANM} = 40^\circ \]. Số đo góc AHD là:
   
   

   Câu hỏi:
   

   Cho hình thang ABCD như hình vẽ. Biết MN // DC, \[\widehat {DAB} = 120^\circ \] và \[\widehat {ANM} = 40^\circ \]. Số đo góc AHD là:
   

   A. 60°;

   B. 40°;

   Đáp án chính xác

   C. 30°;

   D. 125°.

   Trả lời:

   Đáp án đúng là: B
   Vì MN // DC do đó \(\widehat {ANM} = \widehat {AHD}\) (hai góc đồng vị).
   Mà \[\widehat {ANM} = 40^\circ \] nên \[\widehat {AHD} = 40^\circ \].
   Vậy chọn đáp án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình vẽ dưới đây, biết a // b. Tính x, y.
   
   

   Câu hỏi:
   

   Cho hình vẽ dưới đây, biết a // b. Tính x, y.

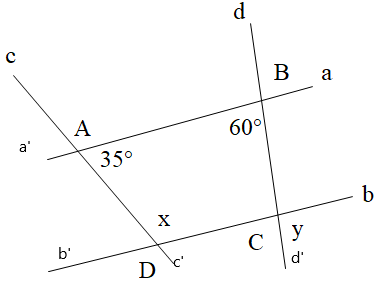
   A. x = 60° và y = 35°;

   B. x = 120° và y = 145°;

   C. x = 35° và y = 60°;

   D. x = 145° và y = 120°.

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: DVì a // b nên \[\widehat {BAD} = \widehat {ADb’} = 35^\circ \] (hai góc so le trong)Mà \[\widehat {ADb’}\] và \[\widehat {ADC}\] là hai góc kề bù nên suy ra \[\widehat {ADC} + \widehat {ADb’} = 180^\circ \Rightarrow x + 35^\circ = 180^\circ \] ^{Suy ra, x = 180o} ‒ 35° = 145°Vì a // b nên \[\widehat {ABC} = \widehat {BCb} = 60^\circ \] (hai góc trong so le trong)Mà \[\widehat {BCb}\] và \[\widehat {bCd’}\] là hai góc kề bù nên suy ra \[\widehat {BCb} + \widehat {bCd’} = 180^\circ \Rightarrow 60^\circ + y = 180^\circ \]Suy ra \[y = 180^\circ – 60^\circ = 120^\circ \]Vậy x = 145° và y = 120°.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====