Câu hỏi:
Cho hình vẽ dưới đây, biết a // b. Tính x, y.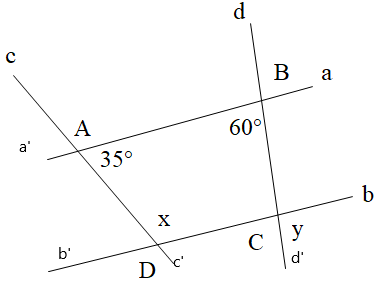
A. x = 60° và y = 35°;
B. x = 120° và y = 145°;
C. x = 35° và y = 60°;
D. x = 145° và y = 120°.
Đáp án chính xác
Trả lời:
Đáp án đúng là: DVì a // b nên \[\widehat {BAD} = \widehat {ADb’} = 35^\circ \] (hai góc so le trong)Mà \[\widehat {ADb’}\] và \[\widehat {ADC}\] là hai góc kề bù nên suy ra \[\widehat {ADC} + \widehat {ADb’} = 180^\circ \Rightarrow x + 35^\circ = 180^\circ \] Suy ra, x = 180o ‒ 35° = 145°Vì a // b nên \[\widehat {ABC} = \widehat {BCb} = 60^\circ \] (hai góc trong so le trong)Mà \[\widehat {BCb}\] và \[\widehat {bCd’}\] là hai góc kề bù nên suy ra \[\widehat {BCb} + \widehat {bCd’} = 180^\circ \Rightarrow 60^\circ + y = 180^\circ \]Suy ra \[y = 180^\circ – 60^\circ = 120^\circ \]Vậy x = 145° và y = 120°.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
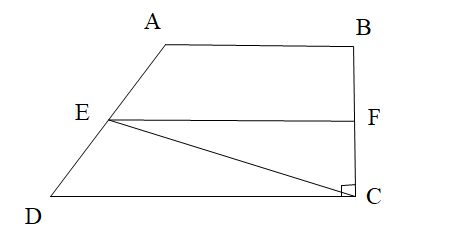
- Cho hình vẽ. Tính góc FEC, biết EF // DC và \[\widehat {ECB} = 60^\circ \]:
Câu hỏi:
Cho hình vẽ. Tính góc FEC, biết EF // DC và \[\widehat {ECB} = 60^\circ \]:
A. 50°;
B. 40°;
C. 60°;
D. 30°.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Vì EF // DC nên ta có: \[\widehat {ECD} = \widehat {F{\rm{E}}C}\] (hai góc so le trong)
Ta có \[\widehat {BCD} = 90^\circ \] hay \[\widehat {FCE} + \widehat {ECD} = 90^\circ \] suy ra \[\widehat {ECD} = 90^\circ – 60^\circ = 30^\circ \].
Do đó \[\widehat {FEC} = \widehat {ECD} = 30^\circ \].
Vậy chọn đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình bình hành ABCD như hình vẽ.
Chọn phương án đúng.
Câu hỏi:
Cho hình bình hành ABCD như hình vẽ.
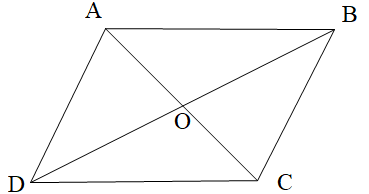
Chọn phương án đúng.A. \[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù;
B. \[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc so le trong;
C. \[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc đồng vị;
D. \[\widehat {AOB}\] và \[\widehat {DOC}\] là hai góc đối đỉnh.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
\[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù là phát biểu sai vì hai góc này không chung đỉnh.
\[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc so le trong là phát biểu sai, vì \[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc kề bù;
\[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc trong cùng phía.
\[\widehat {AOB}\] và \[\widehat {DOC}\] là hai góc đối đỉnh là phát biểu đúng, chọn phương án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình bình hành ABCD như hình vẽ. Biết IJ // DC và \[\widehat {JOC} = 34^\circ \].
Số đo góc OCD là:
Câu hỏi:
Cho hình bình hành ABCD như hình vẽ. Biết IJ // DC và \[\widehat {JOC} = 34^\circ \].
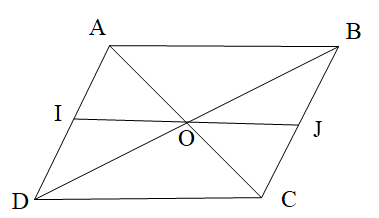
Số đo góc OCD là:A. 60°;
B. 34°;
Đáp án chính xác
C. 40°;
D. 84°.
Trả lời:
Đáp án đúng là: B.
Vì DC // IJ nên ta có: \[\widehat {JOC} = \widehat {OCD}\] (hai góc so le trong).
Do đó \[\widehat {OCD} = \widehat {JOC} = 34^\circ \].
Vậy chọn đáp án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình thang ABCD như hình vẽ. Biết MN // DC, \[\widehat {DAB} = 120^\circ \] và \[\widehat {ANM} = 40^\circ \]. Số đo góc AHD là:
Câu hỏi:
Cho hình thang ABCD như hình vẽ. Biết MN // DC, \[\widehat {DAB} = 120^\circ \] và \[\widehat {ANM} = 40^\circ \]. Số đo góc AHD là:
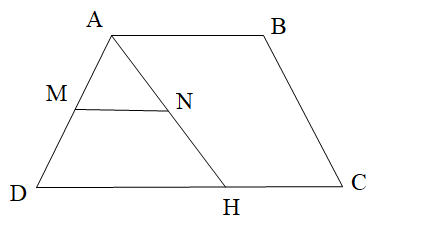
A. 60°;
B. 40°;
Đáp án chính xác
C. 30°;
D. 125°.
Trả lời:
Đáp án đúng là: B
Vì MN // DC do đó \(\widehat {ANM} = \widehat {AHD}\) (hai góc đồng vị).
Mà \[\widehat {ANM} = 40^\circ \] nên \[\widehat {AHD} = 40^\circ \].
Vậy chọn đáp án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \[\widehat {mOn}\] và \[\widehat {nOp}\] là hai góc kề bù. Biết \[\widehat {mOn} = 124^\circ \] và Ot là tia phân giác của góc nOp. Số đo góc mOt là:
Câu hỏi:
Cho \[\widehat {mOn}\] và \[\widehat {nOp}\] là hai góc kề bù. Biết \[\widehat {mOn} = 124^\circ \] và Ot là tia phân giác của góc nOp. Số đo góc mOt là:
A. 152°;
Đáp án chính xác
B. 143°;
C. 45°;
D. 35°.
Trả lời:
Đáp án đúng là: A
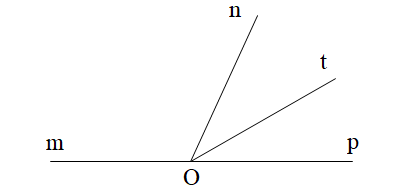
Vì \[\widehat {mOn}\] và \[\widehat {nOp}\] là hai góc kề bù nên \[\widehat {mOn} + \widehat {nOp} = 180^\circ \]
Suy ra \[\widehat {nOp} = 180^\circ – \widehat {mOn}\]
Hay \[\widehat {nOp} = 180^\circ – 124^\circ = 56^\circ \]
Mà \[\widehat {nOt} = \widehat {tOp} = \frac{{\widehat {nOp}}}{2}\] (vì Ot là tia phân giác góc nOp)
Suy ra \[\widehat {nOt} = \widehat {tOp} = \frac{{\widehat {nOp}}}{2} = \frac{{56^\circ }}{2} = 28^\circ \]
Vì hai góc mOn và nOp là hai góc kề bù nên tia On nằm giữa hai tia Om và Op; tia Ot là phân giác của góc nOp nên tia Ot nằm giữa hai tia On và Op.
Do đó tia On nằm giữa hai tia Om và Ot.
Suy ra \[\widehat {mOt} = \widehat {mOn} + \widehat {nOt}\] suy ra \[\widehat {mOt} = 124^\circ + 28^\circ = 152^\circ \].
Do đó \[\widehat {mOt} = 152^\circ \].
Vậy chọn đáp án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====