Câu hỏi:
Hai góc cùng bù với một góc thứ ba thì bằng nhau.
Trả lời:
Hướng dẫn giải:
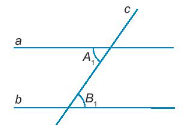
Giả thiết: \(\widehat {xOy} + \widehat {uHv} = 180^\circ \);\(\widehat {x’Oy’} + \widehat {uHv} = 180^\circ \).
Kết luận: \(\widehat {xOy} = \widehat {x’Oy’}\)
Chứng minh:
Ta có: \(\widehat {xOy} + \widehat {uHv} = 180^\circ \) suy ra, \(\widehat {xOy} = 180^\circ – \widehat {uHv}\) (3)
\(\widehat {x’Oy’} + \widehat {uHv} = 180^\circ \) suy ra, \(\widehat {x’Oy’} = 180^\circ – \widehat {uHv}\) (2)
Từ (1) và (2) suy ra: \(\widehat {xOy} = \widehat {x’Oy’}\) = \(180^\circ – \widehat {uHv}\)
Vậy \(\widehat {xOy} = \widehat {x’Oy’}\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho định lí: “Một đường thẳng cắt hai đường thẳng song song thì tạo thành cặp góc so le trong bằng nhau”.
Hãy chỉ ra giả thiết và kết luận của định lí.
Câu hỏi:
Cho định lí: “Một đường thẳng cắt hai đường thẳng song song thì tạo thành cặp góc so le trong bằng nhau”.
Hãy chỉ ra giả thiết và kết luận của định lí.Trả lời:
Lời giải:
Giả thiết: Một đường thẳng cắt hai đường thẳng song song.
Kết luận: Hai góc so le trong tạo thành bằng nhau.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Vẽ hình minh họa và ghi giả thiết, kết luận bằng kí hiệu.
Câu hỏi:
Vẽ hình minh họa và ghi giả thiết, kết luận bằng kí hiệu.
Trả lời:
Hướng dẫn giải:
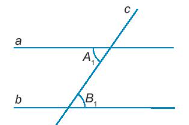
Giả thiết: a // b; c cắt a tại A, c cắt b tại B, tạo thành một cặp góc so le trong \(\widehat {{A_1}};\widehat {{B_1}}\).
Kết luận: \(\widehat {{A_1}} = \widehat {{B_1}}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho định lí: “Một đường thẳng cắt hai đường thẳng tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song”.
Hãy chỉ ra giả thiết và kết luận của định lí.
Câu hỏi:
Cho định lí: “Một đường thẳng cắt hai đường thẳng tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song”.
Hãy chỉ ra giả thiết và kết luận của định lí.Trả lời:
Lời giải:
Giả thiết: Một đường thẳng cắt hai đường thẳng tạo thành cặp góc so le trong bằng nhau.
Kết luận: hai đường thẳng đó song song.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Vẽ hình minh họa và ghi giả thiết, kết luận bằng kí hiệu.
Câu hỏi:
Vẽ hình minh họa và ghi giả thiết, kết luận bằng kí hiệu.
Trả lời:
Hướng dẫn giải:
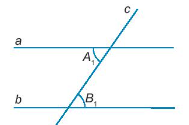
Giả thiết: c cắt a tại A, c cắt b tại B, tạo thành cặp góc so le trong \(\widehat {{A_1}};\widehat {{B_1}}\) và \(\widehat {{A_1}} = \widehat {{B_1}}\)
Kết luận: a // b.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho định lí: “Tia đối của tia phân giác của một góc là tia phân giác của góc đối đỉnh với góc đó”. Hãy vẽ hình ghi giả thiết, kết luận và chứng minh định lí đó.
Câu hỏi:
Cho định lí: “Tia đối của tia phân giác của một góc là tia phân giác của góc đối đỉnh với góc đó”. Hãy vẽ hình ghi giả thiết, kết luận và chứng minh định lí đó.
Trả lời:
Lời giải:
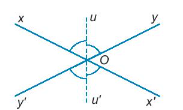
Giả thiết:
– Hai góc xOy; x’Oy’ là hai góc đối đỉnh.
– Ou là tia phân giác của góc xOy, Ou’ là tia đối của tia Ou.
Kết luận: Ou’ là tia phân giác của góc x’Oy’.
Chứng minh định lí:
Ta có:
\(\widehat {x’Ou’}\) và \(\widehat {xOu}\) là hai góc đối đỉnh nên \(\widehat {x’Ou’}\) = \(\widehat {xOu}\).
\(\widehat {y’Ou’}\) và \(\widehat {yOu}\) là hai góc đối đỉnh nên \(\widehat {y’Ou’}\) = \(\widehat {yOu}\).
Lại có: Ou là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOu}\) = \(\widehat {yOu}\).
Suy ra: \(\widehat {x’Ou’}\) = \(\widehat {y’Ou’}\).
Do đó, Ou’ là tia phân giác của \(\widehat {x’Oy’}\).
Vậy Ou’ là tia phân giác của \(\widehat {x’Oy’}\) (điều phải chứng minh).====== **** mời các bạn xem câu tiếp bên dưới **** =====