Câu hỏi:
Cho tam giác ABC có AB = AC, M là trung điểm của BC. Biết \(\widehat {ABC} = 40^\circ ,\) số đo của \(\widehat {BAM}\) là:
A. 20°;
B. 25°;
C. 40°;
D. 50°.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
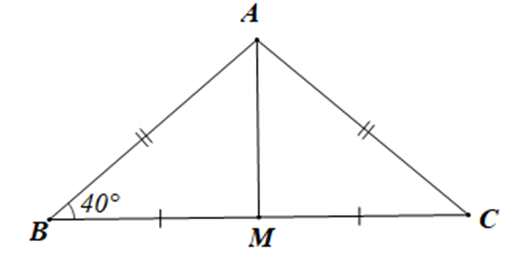
Xét tam giác ABM và tam giác ACM có:
AB = AC (giả thiết),
MB = MC (do M là trung điểm của BC),
AM là cạnh chung
Do đó DABM = DACM (c.c.c)
Suy ra \(\widehat {BAM} = \widehat {CAM},\widehat {AMB} = \widehat {AMC}\) (các cặp góc tương ứng)
Mà \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {AMB} = \widehat {AMC} = \frac{{180^\circ }}{2} = 90^\circ \)
Do đó tam giác ABM vuông tại M
Khi đó \(\widehat {ABM} + \widehat {BAM} = 90^\circ \) (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \(\widehat {BAM} = 90^\circ – \widehat {ABM} = 90^\circ – 40^\circ = 50^\circ .\)
Vậy ta chọn phương án D.
====== **** mời các bạn xem câu tiếp bên dưới **** =====