Câu hỏi:
Cho hình vẽ sau:
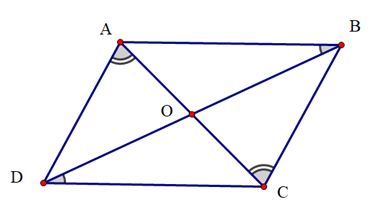
Biết \(\widehat {DAC} = \widehat {ACB}\); \(\widehat {BDC} = \widehat {ABD}\). Có bao nhiêu khẳng định đúng trong các khẳng định sau?
(I). AB // CD;
(II). AD // BC;
(III). AB // BC;
(IV). AC //BD.
A. 1;
B. 2;
Đáp án chính xác
C. 3;
D. 4.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: B
+ Ta có \(\widehat {DAC} = \widehat {ACB}\). Mà hai góc này ở vị trí so le trong.
Suy ra AD // BC
Do đó khẳng định (II) đúng.
+ Ta có \(\widehat {BDC} = \widehat {ABD}\). Mà hai góc này ở vị trí so le trong.
Suy ra AB // CD.
Do đó khẳng định (I) đúng.
+ Ta có AB giao với BC tại điểm B. Do đó AB và BC không song song với nhau.
Do đó khẳng định (III) sai.
+ Ta có AC giao với BD tại điểm O. Do đó AC và BD không song song với nhau.
Do đó khẳng định (IV) sai.
Vậy có 2 khẳng định đúng.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Chứng minh đường thẳng ab song song với cd trong các trường hợp sau:
Câu hỏi:
Chứng minh đường thẳng ab song song với cd trong các trường hợp sau:
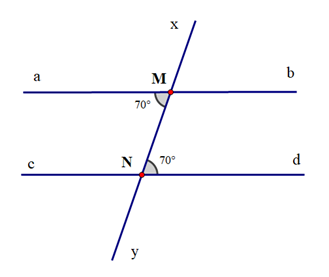
Trả lời:
Hướng dẫn giải:
Ta có \(\widehat {aMN} = \widehat {MNd} = {70^o}\).
Mà \(\widehat {aMN}\) và \(\widehat {MNd}\) là hai góc ở vị trí so le trong.
Do đó ab song song với cd.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Chứng minh đường thẳng ab song song với cd trong các trường hợp sau:
Câu hỏi:
Chứng minh đường thẳng ab song song với cd trong các trường hợp sau:
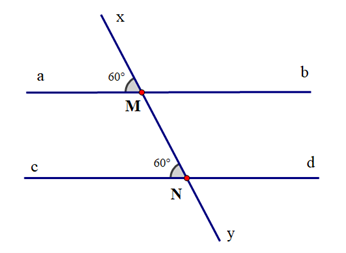
Trả lời:
Hướng dẫn giải:
Ta có \(\widehat {xMa} = \widehat {MNc} = {60^o}\).
Mà \(\widehat {xMa}\) và \(\widehat {MNc}\) là hai góc ở vị trí đồng vị.
Do đó ab song song với cd.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Chứng minh đường thẳng ab song song với cd trong các trường hợp sau:
Câu hỏi:
Chứng minh đường thẳng ab song song với cd trong các trường hợp sau:
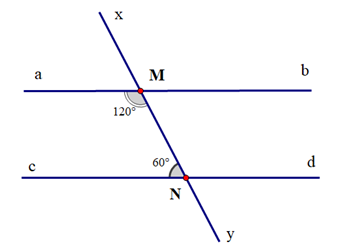
Trả lời:
Hướng dẫn giải:
Ta có \(\widehat {aMN} + \widehat {MNc} = {120^o} + {60^o} = {180^o}\).
Suy ra \(\widehat {aMN}\) và \(\widehat {MNc}\) là hai góc bù nhau.
Mà \(\widehat {aMN}\) và \(\widehat {MNc}\) là hai góc ở vị trí trong cùng phía.
Suy ra ab song song với cd.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Chứng minh đường thẳng ab song song với cd trong các trường hợp sau:
Câu hỏi:
Chứng minh đường thẳng ab song song với cd trong các trường hợp sau:
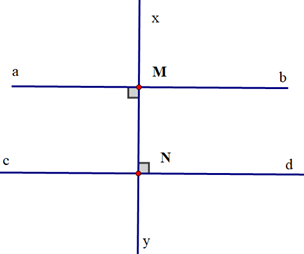
Trả lời:
Hướng dẫn giải:
Vì ab và cd là hai đường thẳng phân biệt cùng vuông góc với đường thẳng xy nên chúng song song với nhau.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình vẽ:
Biết \(\widehat {xAa} = \widehat {yBd} = {45^o}\). Hai đường thẳng ab và cd có song song với nhau không? Vì sao?
Câu hỏi:
Cho hình vẽ:
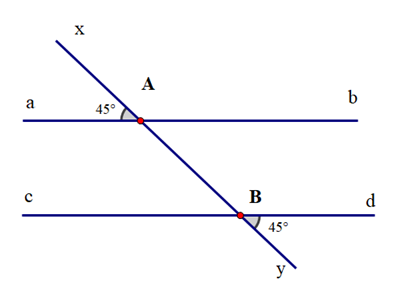
Biết \(\widehat {xAa} = \widehat {yBd} = {45^o}\). Hai đường thẳng ab và cd có song song với nhau không? Vì sao?Trả lời:
Hướng dẫn giải:
Do \(\widehat {xAa}\) và \(\widehat {bAB}\) là hai góc đối đỉnh nên \(\widehat {xAa}\)= \(\widehat {bAB}\) = 45°.
Suy ra \(\widehat {bAB}\) = \(\widehat {dBy}\) (cùng bằng 45°).
Mà \(\widehat {bAB}\) và \(\widehat {dBy}\) là hai góc ở vị trí đồng vị.
Suy ra ab song song với cd.====== **** mời các bạn xem câu tiếp bên dưới **** =====