Câu hỏi:
Cho ∆ABC vuông tại A có AB < AC, \(\widehat B = 60^\circ \). Kẻ AH ⊥ BC (H ∈ BC). Gọi D là điểm trên cạnh AC sao cho AD = AB. Kẻ DE ⊥ BC (E ∈ BC) và DK ⊥ AH (K ∈ AH). Cho các khẳng định sau:
(I) BH = AK;
(II) HA = KD = HE.
Chọn phương án đúng:
A. Chỉ (I) đúng;
B. Chỉ (II) đúng;
C. Cả (I), (II) đều đúng;
Đáp án chính xác
D. Cả (I), (II) đều sai.
Trả lời:
Đáp án đúng là: C
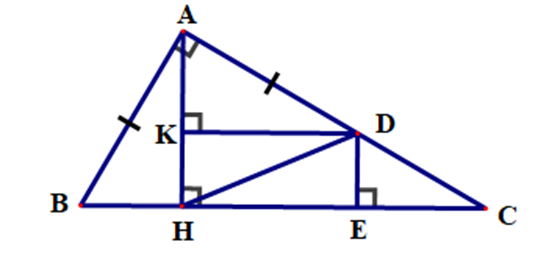
Xét ∆HAB và ∆KDA, có:
\(\widehat {AHB} = \widehat {DKA} = 90^\circ \).
AB = AD (giả thiết).
\(\widehat {BAH} = \widehat {ADK}\) (cùng phụ với \(\widehat {KAD}\)).
Do đó ∆HAB = ∆KDA (cạnh huyền – góc nhọn).
Suy ra HA = KD và BH = AK (các cặp cạnh tương ứng).
Do đó (I) đúng.
Ta có: KD ⊥ AH (giả thiết) và HE ⊥ AH (giả thiết).
Suy ra KD // HE.
Có \(\widehat {KDH},\,\,\widehat {EHD}\) ở vị trí so le trong.
Do đó \(\widehat {KDH} = \widehat {EHD}\).
Xét ∆KDH và ∆EHD, có:
\(\widehat {DKH} = \widehat {HED} = 90^\circ \).
HD là cạnh chung.
\(\widehat {KDH} = \widehat {EHD}\) (chứng minh trên).
Do đó ∆KDH = ∆EHD (cạnh huyền – góc nhọn).
Suy ra KD = EH (hai cạnh tương ứng)
Mà HA = KD (chứng minh trên).
Do đó HA = KD = HE. Suy ra (II) đúng.
Vậy ta chọn đáp án C.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ∆ABC vuông tại A và ∆MNP vuông tại M có AB = MN, CB = PN. Biết AC = 5 cm. Tính độ dài MP.
Câu hỏi:
Cho ∆ABC vuông tại A và ∆MNP vuông tại M có AB = MN, CB = PN. Biết AC = 5 cm. Tính độ dài MP.
A. 4 cm;
B. 5 cm;
Đáp án chính xác
C. 6 cm;
D. 7 cm.
Trả lời:
Đáp án đúng là: B
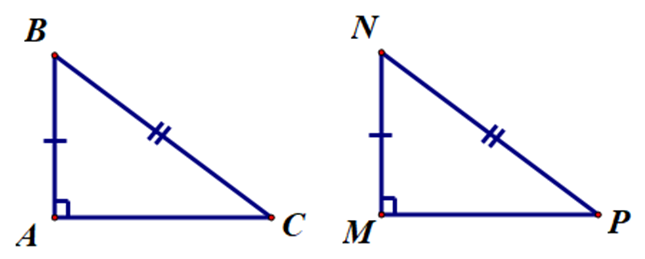
Xét ∆ABC và ∆MNP, có:
\(\widehat {BAC} = \widehat {NMP} = 90^\circ \).
AB = MN (giả thiết).
CB = PN (giả thiết).
Do đó ∆ABC = ∆MNP (cạnh huyền – cạnh góc vuông).
Ta suy ra AC = MP (hai cạnh tương ứng).
Khi đó ta có MP = AC = 5 cm.
Vậy ta chọn đáp án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ∆ABC có AB = AC, đường cao AH. Kết luận nào sau đây sai?
Câu hỏi:
Cho ∆ABC có AB = AC, đường cao AH. Kết luận nào sau đây sai?
A. ∆AHB = ∆AHC theo trường hợp cạnh huyền – góc nhọn;
Đáp án chính xác
B. AH là phân giác \(\widehat {BAC}\);
C. BH = CH;
D. \(\widehat {ABH} = \widehat {ACH}\).
Trả lời:
Đáp án đúng là: A
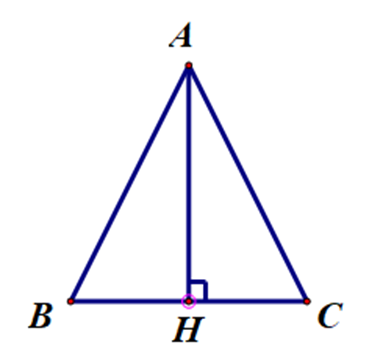
Ta xét từng đáp án:
Đáp án A:
Xét ∆AHB và ∆AHC, có:
\(\widehat {AHB} = \widehat {AHC} = 90^\circ \).
AH là cạnh chung.
AB = AC (giả thiết).
Do đó ∆AHB = ∆AHC (cạnh huyền – cạnh góc vuông).
Ta suy ra đáp án A sai.
Đến đây ta có thể chọn đáp án A.
Đáp án B:
Ta có ∆AHB = ∆AHC (chứng minh trên).
Ta suy ra \(\widehat {BAH} = \widehat {CAH}\) (cặp góc tương ứng).
Do đó AH là phân giác \(\widehat {BAC}\).
Vậy đáp án B đúng.
Đáp án C:
Ta có ∆AHB = ∆AHC (chứng minh trên).
Ta suy ra BH = CH (cặp cạnh tương ứng).
Do đó đáp án C đúng.
Đáp án D:
Ta có ∆AHB = ∆AHC (chứng minh trên).
Ta suy ra \(\widehat {ABH} = \widehat {ACH}\) (cặp góc tương ứng).
Do đó đáp án D đúng.
Vậy ta chọn đáp án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ∆ABC có AI, BH, CK là các đường cao (I ∈ BC, K ∈ AB, H ∈ AC). Biết ∆ABH = ∆ACK. Kết luận nào sau đây đúng?
Câu hỏi:
Cho ∆ABC có AI, BH, CK là các đường cao (I ∈ BC, K ∈ AB, H ∈ AC). Biết ∆ABH = ∆ACK. Kết luận nào sau đây đúng?
A. \(\widehat {HBA} \ne \widehat {KCA}\);
B. HB ≠ KC;
C. \(\widehat {ABH} = \widehat {KAC}\);
D. CH = BK.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
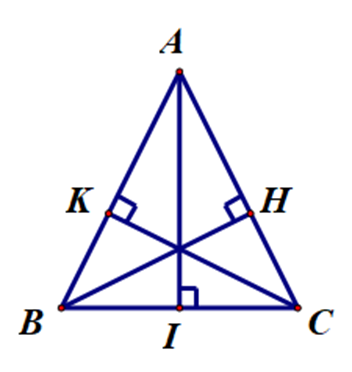
Ta có ∆ABH = ∆ACK (giả thiết).
Ta suy ra \(\widehat {HBA} = \widehat {KCA}\); HB = KC (cặp góc, cặp cạnh tương ứng).
Do đó đáp án A, B sai.
Ta có: ∆ABH = ∆ACK (giả thiết).
Mà \(\widehat {ABH},\,\,\widehat {KAC}\) không phải cặp góc tương ứng.
Do đó \(\widehat {ABH} \ne \widehat {KAC}\).
Suy ra đáp án C sai.
Ta có: ∆ABH = ∆ACK (giả thiết).
Ta suy ra AH = AK và AB = AC (các cặp góc tương ứng).
Do đó AB – AK = AC – AH.
Suy ra BK = CH (vì K ∈ AB, H ∈ AC).
Do đó đáp án D đúng.
Vậy ta chọn đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ∆ABC vuông tại A. Trên cạnh BC, lấy điểm D sao cho BD = BA = 5 cm. Đường thẳng vuông góc với BC tại D cắt AC tại H. Gọi E là giao điểm của DH và AB. Biết CD = 3 cm. Độ dài cạnh BE bằng
Câu hỏi:
Cho ∆ABC vuông tại A. Trên cạnh BC, lấy điểm D sao cho BD = BA = 5 cm. Đường thẳng vuông góc với BC tại D cắt AC tại H. Gọi E là giao điểm của DH và AB. Biết CD = 3 cm. Độ dài cạnh BE bằng
A. 3 cm;
B. 5 cm;
C. 8 cm;
Đáp án chính xác
D. 10 cm.
Trả lời:
Đáp án đúng là: C
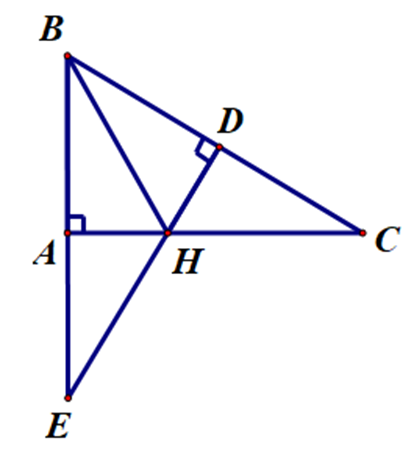
Xét ∆BAH và ∆BDH, có:
\(\widehat {BAH} = \widehat {BDH} = 90^\circ \).
BH là cạnh chung.
BA = BD (giả thiết).
Do đó ∆BAH = ∆BDH (cạnh huyền – cạnh góc vuông).
Ta suy ra AH = DH (cặp cạnh tương ứng).
Xét ∆AHE và ∆DHC, có:
\(\widehat {HAE} = \widehat {HDC} = 90^\circ \).
AH = DH (chứng minh trên).
\(\widehat {AHE} = \widehat {DHC}\) (2 góc đối đỉnh).
Do đó ∆AHE = ∆DHC (cạnh góc vuông – góc nhọn kề).
Ta suy ra AE = DC.
Ta có BA = BD (giả thiết) và AE = DC (chứng minh trên).
Suy ra BA + AE = BD + DC.
Do đó BE = BD + DC = 5 + 3 = 8 (cm).
Vậy ta chọn đáp án C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tìm x trong hình bên.
Câu hỏi:
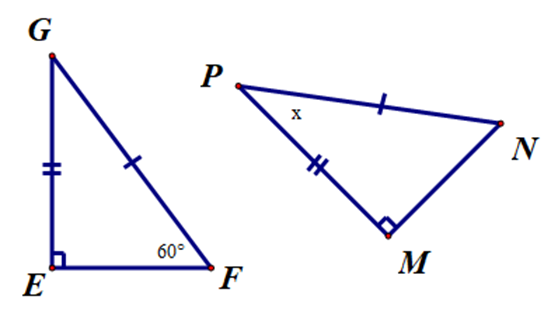
Tìm x trong hình bên.
A. 30°;
Đáp án chính xác
B. 45°;
C. 60°;
D. 90°.
Trả lời:
Đáp án đúng là: A
Xét ∆EFG và ∆MNP, có:
\(\widehat {{\rm{GEF}}} = \widehat {PMN} = 90^\circ \).
GE = PM (giả thiết).
GF = PN (giả thiết).
Do đó ∆EFG = ∆MNP (cạnh huyền – cạnh góc vuông).
Ta suy ra \(\widehat {{\rm{EGF}}} = \widehat {MPN}\) (cặp góc tương ứng).
Hay \(\widehat {{\rm{EGF}}} = x\).
∆EFG vuông tại E: \(\widehat {{\rm{EGF}}} + \widehat {EFG} = 90^\circ \) (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \(\widehat {EGF} = 90^\circ – \widehat {EFG} = 90^\circ – 60^\circ = 30^\circ \).
Do đó x = 30°.
Vậy ta chọn đáp án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====