Câu hỏi:
Chu vi hình bình hành có cạnh bằng 7 cm và 4 cm là
A.11cm;
B.28cm;
C.14cm;
D.22cm.
Đáp án chính xác
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
Chu vi hình bình hành là: 2.(7+4) = 22 (cm)
Vậy chu vi là 22 cm.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Giải Toán 8 Bài 3: Hình thang cân
Giải bài tập Toán lớp 8 Bài 3: Hình thang cân
Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 72 sgk Toán 8 Tập 1: Hình thang () trên hình có gì đặc biệt?
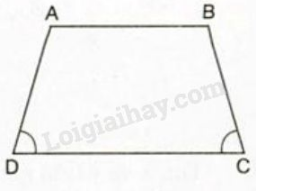
Lời giải:
Hình thang trên hình có hai góc kề cạnh đáy lớn bằng nhau.
Trả lời câu hỏi 2 trang 72 sgk Toán 8 Tập 1: Cho hình 24
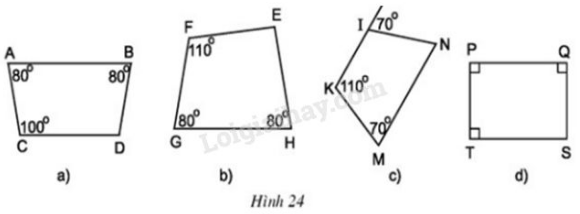
a) Tìm các hình thang cân.
Phương pháp giải: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Lời giải:
+) Xét tứ giác có mà hai góc này ở vị trí trong cùng phía nên . Do đó là hình thang.
Lại có nên hình thang là hình thang cân.
+) Xét tứ giác không có cặp cạnh nào song song nên không là hình thang
+) Xét tứ giác có mà hai góc này ở vị trí trong cùng phía nên . Do đó là hình thang.
Lại có (hai góc kề bù) nên
Suy ra nên là hình thang cân.
+) Xét tứ giác có nên . Do đó là hình thang.
Lại có: nên là hình thang cân.
Vậy có các hình thang cân là:
b) Tính các góc còn lại của mỗi hình thang cân đó.
Phương pháp giải: Áp dụng: Định lí tổng các góc của một tứ giác.
Lời giải:
+) Hình thang cân
Áp dụng định lí tổng các góc của một tứ giác vào tứ giác ta có:
+) Hình thang cân
(theo câu a)
(hai góc so le trong)
+) Hình thang cân
Áp dụng định lí tổng các góc của một tứ giác vào tứ giác ta có:
c) Có nhận xét gì về hai góc đối của hình thang cân?
Phương pháp giải: Hai góc kề bù có tổng số đo bằng .
Lời giải:
Hai góc đối của hình thang cân bù nhau.
Trả lời câu hỏi 3 trang 74 sgk Toán 8 Tập 1: Cho đoạn thẳng và đường thẳng song song với (h.). Hãy vẽ các điểm thuộc sao cho là hình thang có hai đường chéo bằng nhau. Sau đó hãy đo các góc và của hình thang đó để dự đoán về dạng của các hình thang có đường chéo bằng nhau.
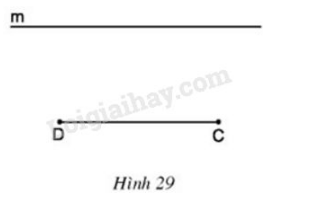
Lời giải:
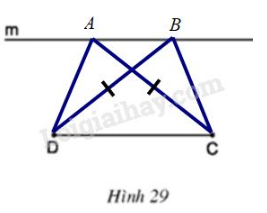
Kết quả đo góc: .
là hình thang cân
Dự đoán: Hình thang có hai đường chéo bằng nhau là hình thang cân.
Câu hỏi và bài tập (trang 74, 75 sgk Toán 8 Tập 1)
Bài 11 trang 74 sgk Toán 8 Tập 1: Tính độ dài các cạnh của hình thang cân trên giấy kẻ ô vuông (h., độ dài cạnh ô vuông là ).
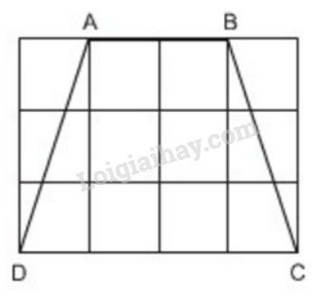
Phương pháp giải: – Áp dụng định lý Pi-ta-go.
– Áp dụng tính chất hình thang cân: Trong hình thang cân hai cạnh bên bằng nhau.
Lời giải:
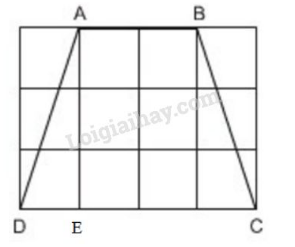
Áp dụng định lý Pitago vào tam giác vuông tại ta được:
Suy ra
là hình thang cân nên (tính chất hình thang cân).
Vậy
Bài 12 trang 74 sgk Toán 8 Tập 1: Cho hình thang cân Kẻ đường cao của hình thang. Chứng minh rằng
Phương pháp giải: +) Tính chất hình thang cân: hình thang cân có hai cạnh bên bằng nhau, hai góc kề đáy bằng nhau.
+) Dấu hiệu nhận biết hai tam giác vuông bằng nhau: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
+) Tính chất hai tam giác bằng nhau: hai cạnh tương ứng bằng nhau.
Lời giải:
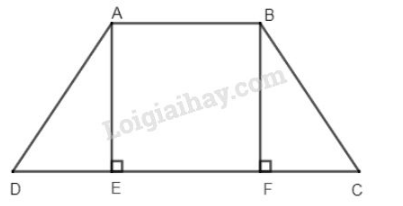
Vì là hình thang cân (giả thiết)
(tính chất hình thang cân)
Xét hai tam giác vuông và có:
+) (chứng minh trên)
+) (chứng minh trên)
Suy ra (cạnh huyền – góc nhọn)
Suy ra: ( cạnh tương ứng).
Bài 13 trang 74 sgk Toán 8 Tập 1: Cho hình thang cân , là giao điểm của hai đường chéo. Chứng minh rằng
Phương pháp giải: – Hình thang cân có hai cạnh bên bằng nhau, hai đường chéo bằng nhau.
– Hai tam giác bằng nhau có các góc tương ứng bằng nhau
– Tam giác cân có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.
Lời giải:
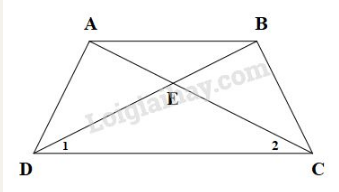
Do là hình thang cân (giả thiết) nên (tính chất hình thang cân)
Xét và
+) (chứng minh trên)
+) (chứng minh trên)
+) chung
Suy ra (c.c.c)
Suy ra ( góc tương ứng)
Do đó cân tại (dấu hiệu nhận biết tam giác cân)
(tính chất tam giác cân)
Lại có:
Trừ vế với vế, ta được
Hay .Vậy
Bài 14 trang 75 sgk Toán 8 Tập 1: Trong các tứ giác và trên giấy kẻ ô vuông (h.), tứ giác nào là hình thang cân? Vì sao?
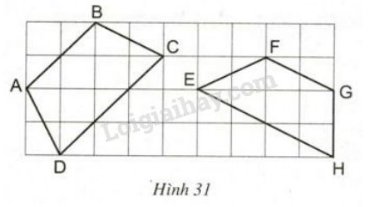
Phương pháp giải:+ Để chứng minh một hình thang là hình thang cân, ta sử dụng một trong các cách sau:
– Chứng minh hai góc kề một đáy bằng nhau
– Chứng minh hai đường chéo bằng nhau
+ Định lý Pytago: vuông tại ta có:
Lời giải:
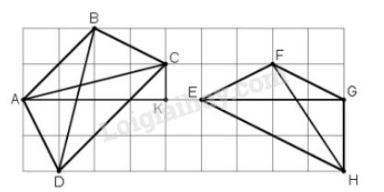
(Coi mỗi cạnh của 1 ô vuông nhỏ là 1cm)
+ Xét tứ giác
Nhận thấy
Tứ giác là hình thang.
Lấy thêm điểm như hình vẽ, ta có
Xét vuông tại , theo định lý Pytago ta có:
Tương tự, từ hình vẽ ta có là cạnh huyền của tam giác vuông có độ dài 2 cạnh góc vuông là 4cm và 1cm.
Theo định lý Pytago ta có:
Vậy hình thang có hai đường chéo nên là hình thang cân.
+ Xét tứ giác
Tứ giác là hình thang.
Lại có: (hình vẽ)
Vì là cạnh huyền của tam giác vuông có độ dài 2 cạnh góc vuông là 2cm và 3cm (hình vẽ) nên theo định lý Pytago ta có:
Vậy hình thang có hai đường chéo không bằng nhau nên không phải hình thang cân.
Bài 15 trang 75 sgk Toán 8 Tập 1: Cho cân tại Trên các cạnh bên lấy theo thứ tự các điểm và sao cho
a) Chứng minh rằng là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng .
Phương pháp giải: – Hình thang là tứ giác có hai cạnh đối song song.
– Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau.
– Định lí tổng ba góc của một tam giác bằng .
– Tam giác cân có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.
Lời giải:
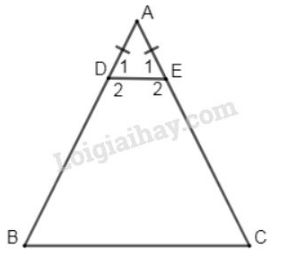
a) Ta có (giả thiết) nên cân (dấu hiệu nhận biết tam giác cân)
= (tính chất tam giác cân)
Xét có: (định lý tổng ba góc trong tam giác)
Vì cân tại (gt) (tính chất tam giác cân)
Mà: (định lý tổng ba góc trong tam giác)
Từ (1) và (2) = , mà hai góc này là hai góc đồng vị nên suy ra (dấu hiệu nhận biết hai đường thẳng song song)
Do đó là hình thang (dấu hiệu nhận biết hình thang).
Lại có ( chứng minh trên )
Nên là hình thang cân (dấu hiệu nhận biết hình thang cân).
b) Với
Ta được
(2 góc trong cùng phía bù nhau)
Mà là hình thang cân (chứng minh trên)
(tính chất hình thang cân)
Bài 16 trang 75 sgk Toán 8 Tập 1: Cho tam giác cân tại , các đường phân giác (). Chứng minh rằng là hình thang cân có đáy nhỏ bằng cạnh bên.
Phương pháp giải: – Hai tam giác bằng nhau có các cạnh tương ứng bằng nhau.
– Tam giác cân có hai cạnh bên bằng nhau và hai góc ở đáy bằng nhau.
– Hai đường thẳng song song khi có cặp góc đồng vị bằng nhau.
– Hình thang là tứ giác có hai cạnh đối song song.
– Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau.
Lời giải:
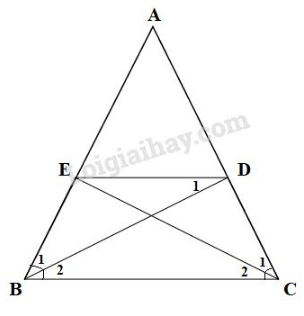
cân tại (giả thiết)
(tính chất tam giác cân)
Vì lần lượt là phân giác của và (giả thiết)
(tính chất tia phân giác)
Mà (chứng minh trên)
Xét và có:
+) (chứng minh trên)
+) chung
+) (chứng minh trên)
( cạnh tương ứng).
Ta có (chứng minh trên) nên cân tại (dấu hiệu nhận biết tam giác cân)
(tính chất tam giác cân)
Xét có: (định lý tổng ba góc trong tam giác)
Xét có: (định lý tổng ba góc trong tam giác)
Mà (chứng minh trên)
Từ (1) và (2) = , mà hai góc này là hai góc đồng vị nên suy ra (dấu hiệu nhận biết hai đường thẳng song song)
Do đó là hình thang (dấu hiệu nhận biết hình thang).
Lại có = (chứng minh trên)
Nên là hình thang cân (dấu hiệu nhận biết hình thang cân)
Ta có:
(so le trong)
Lại có = (chứng minh trên) nên =
cân tại (dấu hiệu nhận biết tam giác cân)
(tính chất tam giác cân).
Vậy là hình thang cân có đáy nhỏ bằng cạnh bên.
Bài 17 trang 75 sgk Toán 8 Tập 1: Hình thang có . Chứng minh rằng là hình thang cân.
Phương pháp giải: – Tam giác cân là tam giác có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.
– Dấu hiệu nhận biết hình thang cân: Hình thang có hai đường chéo bằng nhau là hình thang cân
Lời giải:
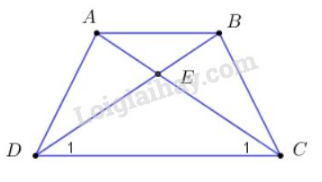
Gọi là giao điểm của và
Xét có: (giả thiết)
cân tại (dấu hiệu nhận biết tam giác cân).
(tính chất tam giác cân) (1)
Ta có:
Mà: cân tại (dấu hiệu nhận biết tam giác cân)
(tính chất tam giác cân) (2)
Lại có:
Từ (1), (2) và (3) suy ra
Suy ra hình thang là hình thang cân (dấu hiệu nhận biết hình thang).
Bài 18 trang 75 sgk Toán 8 Tập 1: Chứng minh định lí “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau: Cho hình thang có
Qua kẻ đường thẳng song song với , cắt đường thẳng tại Chứng mình rằng:
a) là tam giác cân.
b)
c) Hình thang là hình thang cân.
Phương pháp giải: Áp dụng:
– Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau.
– Tam giác cân có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.
– Nhận xét: Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
Lời giải:
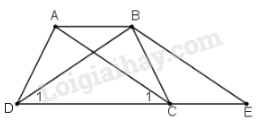
a) thuộc đường thẳng nên
Hình thang có hai cạnh bên song song (giả thiết) (1) (nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau )
Lại có: (giả thiết) (2)
Từ (1) và (2) suy ra cân tại (dấu hiệu nhận biết tam giác cân).
b) Ta có (2 góc đồng vị) (3)
cân tại (chứng minh trên) (4)
Từ (3) và (4)
Xét và có:
+) (giả thiết)
+) (chứng minh trên)
+) chung
Suy ra (c.g.c)
c) Ta có: (chứng minh trên)
( góc tương ứng)
Hình thang có hai góc kề một đáy bằng nhau nên là hình thang cân.
Bài 19 trang 75 sgk Toán 8 Tập 1: Đố. Cho ba điểm trên giấy kẻ ô vuông (h.). Hãy tìm điểm thứ tư là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình thang cân
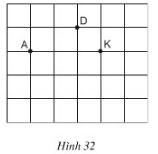
Lời giải:
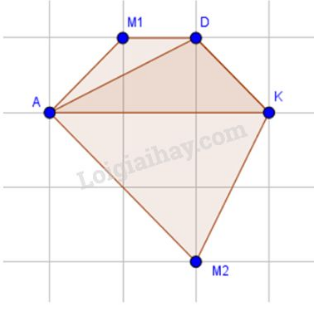
Có thể tìm được hai điểm là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình thang cân. Đó là hình thang (với là hai đáy) và hình thang (với là hai đáy).
Lý thuyết hình thang cân
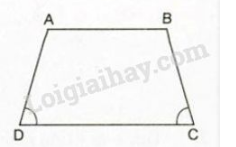
1. Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Ví dụ: là hình thang cân (đáy )
và
2. Tính chất:
Định lí 1: Trong một hình thang cân, hai cạnh bên bằng nhau.
Ví dụ: là hình thang cân (đáy )
Định lí 2: Trong một hình thang cân, hai đường chéo bằng nhau.
Ví dụ: là hình thang cân (đáy )
Định lí 3: Trong hình thang cân, hai góc kề 1 đáy bằng nhau
Ví dụ: Hình thang (đáy ) và
3. Dấu hiệu nhận biết hình thang cân:
– Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
– Hình thang có hai đường chéo bằng nhau là hình thang cân.
- Giáo án Hình thang cân (2023) – Toán 8
Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:
Giáo án Toán 8 Bài 3: Hình thang cân
A. Mục tiêu
1. Kiến thức:
– HS phát biểu được các định nghĩa, tính chất, các dấu hiệu nhận biết về hình thang cân.
2. Kỹ năng:
– HS phân loại được Hình thang cân, biết vẽ hình thang cân, biết sử dụng định nghĩa, các tính chất vào chứng minh, biết chứng minh 1 tứ giác là hình thang cân.
3. Thái độ:
– Tích cực, tự giác, hợp tác.
4. Phát triển năng lực:
– Năng lực giải quyết vấn đề: HS phân tích được tình huống học tập, phát hiện và nêu được tình huống có vấn đề, đề xuất được giải pháp giải quyết, nhận ra được sự phù hợp hay không phù hợp của giải pháp thực hiện.
– Năng lực tính toán: HS biết tính toán cho phù hợp.
– Năng lực hợp tác: HS biết hợp tác, hỗ trợ nhau trong nhóm để hoàn thành phần việc được giao ; biết nêu những mặt được và mặt thiếu sót của cá nhân và cả nhóm.
– Năng lực vẽ hình, chứng minh.
B. Chuẩn bị
1. Giáo viên:
– Compa, thước, tranh vẽ, bảng phụ..
2. Học sinh:
– Compa, thước, bảng nhóm.
C. Phương pháp
– Vấn đáp, nêu và giải quyết vấn đề, thuyết trình, …
D. Tiến trình dạy học
1. Tổ chức lớp: Kiểm diện.
2. Kiểm tra bài cũ:
3. Bài mới
Hoạt động của giáo viên
Hoạt động của học sinh
Ghi bảng
Hoạt động 1: Khởi động (5’)
– Treo bảng phụ – Gọi một HS lên bảng
– Kiểm btvn vài HS
– Cho HS nhận xét
– Nhận xét đánh giá và vào bài
– HS làm theo yêu cầu của GV:
– Một HS lên bảng trả lời
x =1800 – 110= 700
y =1800 – 110= 700
– HS nhận xét bài làm của bạn
– HS ghi nhớ, tự sửa sai (nếu có)
1- Định nghĩa hình thang (nêu rõ các yếu tố của nó) (4đ)
2- Cho ABCD là hình thang (đáy là AB và CD). Tính x và y (6đ)
Hoạt động 2: Hình thành kiến thức
– Có nhận xét gì về hình thang trên (trong đề ktra)?
– GV giới thiệ hình thang cân cho HS phát biểu định nghĩa.
– GV tóm tắt ý kiến và ghi bảng
– Đưa ra ?2 trên bảng phụ (hoặc phim trong)
– GV chốt lại bằng cách chỉ trên hình vẽ và giải thích từng trường hợp
– Qua ba hình thang cân trên, có nhận xét chung là gì?
– HS quan sát hình và trả lời (hai góc ở đáy bằng nhau)
– HS suy nghĩ, phát biểu …
– HS phát biểu lại định nghĩa
– HS suy nghĩ và trả lời tại chỗ
– HS khác nhận xét
– Tương tự cho câu b, c
– Quan sát, nghe giảng
– HS nêu nhận xét: hình thang cân có hai góc đối bù nhau.
1. Định nghĩa:
Hình thang cân là hình thang có 2 góc kề 1 đáy bằng nhau
Hình thang cân ABCD:
– Cho HS đo các cạnh bên của ba hình thang cân ở hình 24. Từ đó rút ra nhận xét.
– Ta chứng minh điều đó ?
– GV vẽ hình, cho HS ghi GT, KL
– Trường hợp cạnh bên AD và BC không song song, kéo dài cho chúng cắt nhau tại O các DODC và OAB là tam giác gì?
– Thu vài phiếu học tập, cho HS nhận xét ở bảng
– Trường hợp AD//BC ?
– GV: hthang có hai cạnh bên song song thì hai cạnh bên bằng nhau. Ngược lại, hình thang có hai cạnh bên bằng nhau có phải là hình thang cân không?
– Treo hình 27 và nêu chú ý (sgk)
– Mỗi HS tự đo và nhận xét.
– HS nêu định lí
– HS suy nghĩ, tìm cách c/minh
– HS vẽ hình, ghi GT-KL
– HS nghe gợi ý
– Một HS lên bảng chứng minh trường hợp a, cả lớp làm vào phiếu học tập
– HS nhận xét bài làm ở trên bảng
– HS suy nghĩ trả lời
– HS suy nghĩ trả lời
– HS ghi chú ý vào vở
2.Tính chất:
a) Định lí 1:
Trong hình thang cân, hai cạnh bên bằng nhau
Chứng minh: (sgk trang 73)
Chú ý: (sgk trang 73)
– Treo bảng phụ (hình 23sgk)
– Theo định lí 1, hình thang cân ABCD có hai đoạn thẳng nào bằng nhau ?
– Dự đoán như thế nào về hai đường chéo AC và BD?
– Ta phải cminh định lísau
– Vẽ hai đường chéo, ghi GT-KL?
– Em nào có thể chứng minh ?
– GV chốt lại và ghi bảng
– HS quan sát hình vẽ trên bảng
– HS trả lời (ABCD là hình thang cân, theo định lí 1 ta có AD = BC)
– HS nêu dự đoán … (AC = BD)
– HS đo trực tiếp 2 đoạn AC, BD
– HS vẽ hình và ghi GT-KL
– HS trình bày miệng tại chỗ
– HS ghi vào vở
b) Định lí 2:
Trong hình thang cân, hai đường chéo bằng nhau
Cm: (sgk trang73)
– GV cho HS làm ?3
– Làm thế nào để vẽ được 2 điểm A, B thuộc m sao cho ABCD là hình thang có hai đường chéo AC = BD? (gợi ý: dùng compa)
– Cho HS nhận xét và chốt lại:
+ Cách vẽ A, B thoã mãn đk
+ Phát biểu định lí 3 và ghi bảng
– Dấu hiệu nhận biết hthang cân?
– GV chốt lại, ghi bảng
– HS đọc yêu cầu của ?3
– Mỗi em làm việc theo yêu cầu của GV:
+ Vẽ hai điểm A, B
+ Đo hai góc C và D
+ Nhận xét về hình dạng của hình thang ABCD.
(Một HS lên bảng, còn lại làm việc tại chỗ)
– HS nhắc lại và ghi bài
– HS nêu …
3. Dấu hiệu nhận biết hình thang cân:
a) Định Lí 3: Sgk trang 74
b) Dấu hiệu nhận biết hình thang cân:
1. Hình thang có góc kề một đáy bằng nhau là hthang cân
2. Hình thang có hai đường chéo bằng nhau là hthang cân
Hoạt động 3: Luyện tập
– Học bài: thuộc định nghĩa, các tính chất, dấu hiệu nhận biết
– Bài tập 12 trang 74 Sgk
! Các trường hợp bằng nhau của tam giác.
– Bài tập 13 trang 74 Sgk
! Tính chất hai đường chéo hình thang cân và phương pháp chứng minh tam giác cân
– Bài tập 15 trang 75 Sgk
– HS nghe dặn
– 3 trường hợp bằng nhau của tam giác
– HS ghi chú vào vở
– Bài tập 12 trang 74 Sgk
– Bài tập 13 trang 74 Sgk
– Bài tập 15 trang 75 Sgk
Hoạt động 4: Vận dụng
– Yêu cầu HS nhắc lại định nghĩa hình thang cân, hai tính chất của hình thang cân.
– Muốn chứng minh một tứ giác là hình thang cân có mấy cách ? Kể ra ?
– HS trả lời như SGK.
– Muốn chứng minh một tứ giác là hình thang cân có hai cách: Chứng minh tứ giác đó là hình thang có góc kề đáy bằng nhau hoặc chứng minh tứ giác đó là hình thang có hai đường chéo bằng nhau.
5. MỞ RỘNG
Vẽ sơ đồ tư duy khái quát nội dung bài học.
Sưu tầm và làm một số bài tập nâng cao.
Làm bài tập phần mở rộng.
5. Hướng dẫn học sinh tự học (1p)
– Học bài và làm bài tập đầy đủ.
– Ôn tập và nắm chắc các Định nghĩa, tính chất, dấu hiệu nhận biết Hình thang cân.
– Hiểu rõ và nắm chắc định lý và cách chứng minh 3 định lý đó.
– BTVN: BT12+13+14+15+18 (SGK.T74+75).
BT24+30+31 (SBT.T63).
- Giao án Luyện tập Hình thang cân (2023) – Toán 8
Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:
Giáo án Luyện tập Toán 8 Bài 3: Hình thang cân
A. Mục tiêu
1. Kiến thức:
– HS phát biểu được và nắm vững, củng cố các định nghĩa, các tính chất của hình thang, các dấu hiệu nhận biết của hình thang cân.
2. Kỹ năng:
– Nhận biết hình thang cân, biết vẽ hình thang cân, biết sử dụng các định nghĩa, các tính chất của hình thang, các dấu hiệu nhận biết, các tính chất vào chứng minh các đoạn thằng bằng nhau, các góc bằng nhau dựa vào dấu hiệu đã học. Biết cách chứng minh 1 tứ giác là hình thang cân theo điều kiện cho trước. Rèn luyện cách phân tích xác định phương hướng chứng minh.
3. Thái độ:
– Rèn tư duy suy luận ra được 4 góc ngoài của tứ giác là 360o.
4. Phát triển năng lực:
– Năng lực giải quyết vấn đề: HS phân tích được tình huống học tập, phát hiện và nêu được tình huống có vấn đề, đề xuất được giải pháp giải quyết, nhận ra được sự phù hợp hay không phù hợp của giải pháp thực hiện.
– Năng lực tính toán: HS biết tính toán cho phù hợp.
– Năng lực hợp tác: HS biết hợp tác, hỗ trợ nhau trong nhóm để hoàn thành phần việc được giao ; biết nêu những mặt được và mặt thiếu sót của cá nhân và cả nhóm.
– Năng lực vẽ hình + chứng minh hình học.
B. Chuẩn bị
1. Giáo viên:
– Compa, thước, bảng phụ..
2. Học sinh:
– Compa, thước, bảng nhóm.
C. Phương pháp
– Vấn đáp, nêu và giải quyết vấn đề, thuyết trình, …
D. Tiến trình dạy học
1. Tổ chức lớp: Kiểm diện.
2. Kiểm tra bài cũ:
– HS1: Phát biểu định nghĩa hình thang cân và các tính chất của nó.
– HS2: Muốn c/m 1 hình thang nào đó là hình thang cân thì ta phải chứng minh những điều kiện nào?
– HS3: Muốn c/m 1 tứ giác nào đó là hình thang cân thì ta phải chứng minh như thế nào?
3. Bài mới
Hoạt động của giáo viên
Hoạt động của học sinh
Ghi bảng
Hoạt động 1: Khởi động (12’)
– Cho HS chữa bài 15 (trang 75)
– GV kiểm bài làm ở nhà của một vài HS
– Cho HS nhận xét ở bảng
– Đánh giá; khẳng định những chỗ làm đúng; sửa lại những chỗ sai của HS và yêu cầu HS nhắc lại cách c/m 1 tứ giác là hthang cân
– Qua bài tập, rút ra một cách vẽ hình thang cân?
– Một HS vẽ hình; ghi GT-KL một HS trình bày lời giải
– Cả lớp theo dõi
– HS nêu ý kiến nhận xét, góp ý bài làm trên bảng
– HS sửa bài vào vở
– HS nhắc lại cách chứng minh hình thang cân
– HS nêu cách vẽ hình thang cân từ một tam giác cân
Bài 15 trang 75 Sgk
Hoạt động 2: Luyện tập (28’)
– Cho HS đọc đề bài, GV vẽ hình lên bảng, gọi HS tóm tắt gt-kl
– Chứng minh ABCD là hình thang cân như thế nào?
– Với điều kiện , ta có thể chứng minh được gì? =>
– Cần chứng minh thêm gì nữa?
=> ?
– Từ đó => ?
– Gọi 1 HS giải; HS khác làm vào nháp
– Cho HS nhận xét ở bảng
– GV hoàn chỉnh bài cho HS
– HS đọc đề bài, vẽ hình và tóm tắt Gt-Kl.
– Hình thang ABCD có AC=BD
DODC cân
=> OD=OC
– Cần chứng minh DOAB cân
=> OA=OB
AC=BD
Gọi O là giao điểm của AC và BD, ta có:
– Nhận xét bài làm ở bảng
– Sửa bài vào vở
Bài 17 trang 75 Sgk
Giải
Gọi O là giao điểm của AC và BD, ta có:
Bài 18 trang 75 Sgk
Hoạt động 3: Vận dụng (3’)
– Gọi HS nhắc lại các kiến thức đã học trong §2, §3.
– Chốt lại cách chứng minh hình thang cân
– HS nêu định nghĩa hình thang, hình thang cân. Tính chất và dấu hiệu nhận biết hình thang cân
Hoạt động 4: Mở rộng (2’)
– Ôn kiến thức về hình thang, hình thang cân
– Bài tập 16 trang 75 Sgk
! Sử dụng dấu hiệu nhận biết
– Bài tập 19 trang 75 Sgk
– HS nghe dặn
– HS ghi chú vào vở
– Bài tập 16 trang 75 Sgk
– Bài tập 19 trang 75 Sgk
4. Hướng dẫn học sinh tự học (1p)
– Làm các bài tập 17, 19(SGK)
– Đọc bài đường trung bình của tam giác, của hình thang.
- Lý thuyết Hình thang cân (Cánh diều 2023) hay, chi tiết | Toán lớp 6
Lý thuyết Toán lớp 6 Bài 4: Hình thang cân
A. Lý thuyết Hình thang cân
I. Nhận biết Hình thang cân
Cho Hình thang cân ABCD
Khi đó Hình thang cân ABCD có:
+ Hai cạnh đáy AB và CD song song với nhau;
+ Hai cạnh bên bằng nhau: AD = BC; hai đường chéo bằng nhau: AC = BD;
+ Hai góc kề với đáy AB bằng nhau, tức là hai góc DAB và CBA bằng nhau; hai góc kề với đáy CD bằng nhau, tức là hai góc ADC và góc BCD bằng nhau.
II. Chu vi và diện tích Hình thang cân
(Hình thang cân có hai cạnh bên bằng nhau)
– Chu vi của Hình thang cân bằng tổng độ dài các cạnh của Hình thang cân đó
C = a + b + c + c = a + b + 2c
– Diện tích của Hình thang cân bằng tổng độ dài hai cạnh đáy nhân với chiều cao rồi chia đôi
.
B. Bài tập tự luyện
Bài 1. Cho Hình thang cân PQRS có độ dài đáy PQ = 10 cm, đáy RS ngắn hơn đáy PQ là 6 cm, độ dài cạnh bên PS bằng một nửa độ dài đáy PQ. Tính chu vi của Hình thang cân PQRS.
Lời giải:
Đáy RS ngắn hơn đáy PQ là 6 cm nên độ dài đáy RS là:
10 – 6 = 4 (cm)
Độ dài cạnh bên PS bằng một nửa độ dài đáy PQ nên độ dài cạnh bên PS là:
10 : 2 = 5 (cm)
Vì PQRS là Hình thang cân nên hai cạnh bên PS và QR bằng nhau
Nên QR = PS = 5 cm.
Chu vi của Hình thang cân PQRS là:
PQ + RS + QR + PS = 10 + 4 + 5 + 5 = 24 (cm)
Vậy chu vi của hình thang PQRS là 24 cm.
Bài 2. Cho Hình thang cân ABCD có độ dài đáy AB bằng 4 cm, độ dài đáy CD gấp đôi độ dài đáy AB, độ dài chiều cao AH bằng 3 cm. Tính diện tích Hình thang cân ABCD.
Lời giải:
Độ dài đáy CD gấp đôi độ dài đáy AB nên độ dài đáy CD là:
4 . 2 = 8 (cm)
Ta có: AB = 4 cm; CD = 8 cm; AH = 3 cm. Do đó diện tích Hình thang cân ABCD là:
(cm2)
Vậy diện tích Hình thang cân ABCD là 18 cm2.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 3: Hình bình hành
Lý thuyết Bài 4: Hình thang cân
Lý thuyết Bài 5: Hình có trục đối xứng
Lý thuyết Bài 6: Hình có tâm đối xứng
Lý thuyết Bài 7: Đối xứng trong thực tiễn
- Sách bài tập Toán 6 Bài 4 (Cánh diều): Hình thang cân
Giải SBT Toán lớp 6 Bài 4: Hình thang cân
Bài 26 trang 112 sách bài tập Toán lớp 6 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Hình thang cân có hai cạnh bên bằng nhau và hai đường chéo bằng nhau.
b) Hình thang cân có hai cạnh bên bằng nhau và hai đường chéo không bằng nhau.
c) Có vô số hình thang cân mà độ dài đáy lớn gấp hai lần độ dài đáy bé.
Lời giải:
Phát biểu a) là pháp biểu đúng.
Phát biểu b) là sai vì hai đường chéo của hình thang cân bằng nhau.
Phát biểu c) là đúng.
Bài 27 trang 113 sách bài tập Toán lớp 6 Tập 1: Trong Hình 29, các hình từ a) đến e), hình nào là hình thang cân?
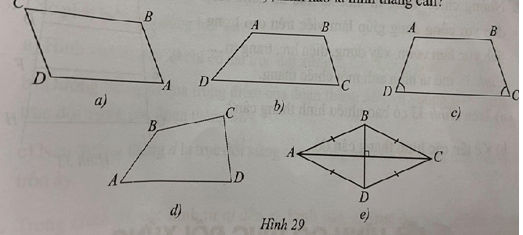
Lời giải:
Trong các hình đã cho, hình 29c) là hình thang cân vì có hai đáy song song và có hai góc kề một đáy bằng nhau.
Bài 28 trang 113 sách bài tập Toán lớp 6 Tập 1: Cho hình thang cân ABCD với độ dài cạnh đáy AB = 6cm. Trung bình cộng của hai đáy bằng 9cm. Độ dài cạnh bên kém độ dài cạnh đáy CD là 7cm (Hình 30). Tính chu vi của hình thang cân ABCD.
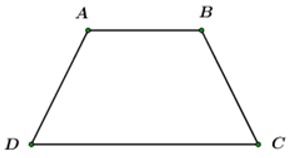
Hình 30
Lời giải:
Độ dài cạnh CD là: 9.2 – 6 = 18 – 6 = 12 cm.
Độ dài hai cạnh bên AD bằng CB và bằng: 12 – 7 = 5 cm.
Chu vi hình thang cân ABCD là: 6 + 5 + 12 + 5 = 28 cm.
Vậy chu vi hình thang cân ABCD là 28cm.
Bài 29 trang 113 sách bài tập Toán lớp 6 Tập 1: Cho hình thang cân MNPQ với trung bình cộng của hai đáy bằng 10cm. Đáy lớn dài hơn đáy nhỏ 8cm. Độ dài chiều cao hơn độ dài đáy nhỏ 2cm. Tính diện tích hình thang cân MNPQ.
Lời giải:
Tổng độ dài hai đáy là: 10.2 = 20 (cm).
Độ dài đáy nhỏ của là: (10.2 – 8):2 = 6 (cm).
Độ dài đáy lớn là: 6 + 8 = 14 (cm).
Chiều cao là: 6 + 2 = 8 (cm).
Diện tích hình thang cân MNPQ là: (6 + 14).8:2 = 80 (cm2).
Vậy diện tích hình thang cân MNPQ là: 80 cm2.
Bài 30 trang 113 sách bài tập Toán lớp 6 Tập 1: Cho hình thang cân ABCD, biết mỗi ô vuông có cạnh 1cm (Hình 31).
a) Tính diện tích hình thang cân ABCD.
b) Diện tích tam giác BDC gấp mấy lần diện tích tam giác ADE?
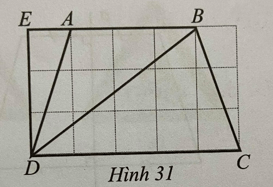
Lời giải:
a)
Độ dài đáy lớn CD là: 5 cm.
Độ dài đáy nhỏ AB là: 3 cm.
Chiều cao của hình thang ABCD bằng cạnh ED bằng 3 cm.
Diện tích hình thang ABCD là: (5 + 3).3:2 = 12 cm2.
b)
Tam giác BCD có đáy CD bằng 5cm và chiều cao bằng cạnh ED bằng 3cm.
Tam giác ADE có đáy AE bằng 1 cm và chiều cao là ED bằng 3cm.
Vậy diện tích tam giác BCD gấp 5 lần diện tích tam giác ADE.
Bài 31 trang 113 sách bài tập Toán lớp 6 Tập 1: Bác Đức dự định mua loại gỗ giá 100 đồng/cm2 để làm một chiếc bàn như Hình 32. Mặt bàn là một hình thang cân có các đáy lần lượt là 90cm, 120cm và chiều cao 80cm. Hãy tính giúp bác Đức số tiền mua gỗ để đóng mặt bàn đó.
Lời giải:
Diện tích mặt bàn là: (90 + 120).80:2 = 8 400 (cm2).
Số tiền mua gỗ để đóng mặt bàn đó: 8 400. 100 = 840 000 (đồng).
Vậy bác Đức cần 8 400 000 đồng mua gỗ để đóng mặt bàn đó.
Bài 32 trang 114 sách bài tập Toán lớp 6 Tập 1: Những chiếc thang từ thời xa xưa đã được biết đến với công dụng giúp làm việc trên cao trong lĩnh vực làm vườn, xây dựng, điện lực, trang trí, … Hình 33 mô tả hình ảnh một chiếc thang.
a) Trên Hình 33 có bao nhiêu hình thang cân?
b) Kể tên các hình thang cân đó.
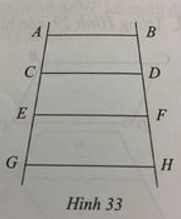
Lời giải:
a) Có tất cả 6 hình thang cân.
b) Các hình thang cân là: ABCD, ABFE, ABHG, CDFE, CDHG, EFHG.