Kí hiệu: Cnk (với k; n là những số nguyên dương và k ≤ n) có ý nghĩa là

Câu hỏi:

Kí hiệu: $C_n^k$ (với k; n là những số nguyên dương và k $\le$ n) có ý nghĩa là

A. Chỉnh hợp chập k của n phần tử.

B. Số tổ hợp chập k của n phần tử.

Đáp án chính xác

C. Tổ hợp chập k của n phần tử.

D. Số chỉnh hợp chập k của n phần tử.

Trả lời:

Chọn B

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Một chiếc vòng đeo tay gồm 20 hạt giống nhau. Hỏi có bao nhiêu cách cắt chiếc vòng đó thành 2 phần mà số hạt ở mỗi phần đều là số lẻ? 
   
   

   Câu hỏi:
   

   Một chiếc vòng đeo tay gồm 20 hạt giống nhau. Hỏi có bao nhiêu cách cắt chiếc vòng đó thành 2 phần mà số hạt ở mỗi phần đều là số lẻ? 

   A. 90.

   B. 5.

   Đáp án chính xác

   C. 180.

   D. 10 .

   Trả lời:

   Chọn B
   Ta có: 20 = 1 + 19 = 3 + 17 = 5 + 15 = 7 + 13 mà vòng đeo tay gồm 20 hạt giống nhau nên có 5 cách cắt chiếc vòng đó thành 2 phần mà số hạt ở mỗi phần đều là số lẻ.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho đa giác đều 2019 đỉnh. Khi đó số tứ giác mà mỗi đỉnh được lấy từ các đỉnh của đa giác đều đã cho và không có cạnh nào là cạnh của đa giác đều đã cho là:
   
   

   Câu hỏi:
   

   Cho đa giác đều 2019 đỉnh. Khi đó số tứ giác mà mỗi đỉnh được lấy từ các đỉnh của đa giác đều đã cho và không có cạnh nào là cạnh của đa giác đều đã cho là:

   A. $2019C_{2016}^4$

   B. $2019C_{2019}^4$– 2019

   C. 504,75$2019C_{2016}^4$

   Đáp án chính xác

   D. $2019C_{2019}^4$

   Trả lời:

   Chọn C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Một công việc để hoàng thành bắt buộc phải trải qua hai bước, bước thứ nhất có m cách thực hiện và bước thứ hai có n cách thực hiện. Số cách để hoàn thành công việc đã cho bằng
   
   

   Câu hỏi:
   

   Một công việc để hoàng thành bắt buộc phải trải qua hai bước, bước thứ nhất có m cách thực hiện và bước thứ hai có n cách thực hiện. Số cách để hoàn thành công việc đã cho bằng

   A. m + n

   B. $m^n$

   C. mn

   Đáp án chính xác

   D. $n^m$

   Trả lời:

   Chọn C
   Theo quy tắc nhân ta có số cách là mn

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Từ các chữ số 1,2,3,….,9 lập được bao nhiêu số có 3 chữ số đôi một khác nhau.
   
   

   Câu hỏi:
   

   Từ các chữ số 1,2,3,….,9 lập được bao nhiêu số có 3 chữ số đôi một khác nhau.

   $A. 3^9$

   $B. A_9^3$

   Đáp án chính xác

   $C. 9^3$

   $D. C_9^3$

   Trả lời:

   Chọn B
   Lấy ra 3 chữ số từ 9 chữ số và sắp xếp 3 chữ số đó theo thứ tự, mỗi cách sắp xếp tạo nên 1 số có 3 chữ số khác nhau. Như vậy, có $A_9^3$ số cần tìm.
   * Nhận xét: Mục đích bài toán là phân biệt hai khái niệm: Chỉnh hợp và tổ hợp. Học sinh có thể giải bài này bằng phương pháp nhân: 9.8.7, và so sánh với 4 đáp án. Hai chỉnh hợp khác nhau thì có thể khác nhau về phần tử hoặc khác nhau về thứ tự các phần tử. Hai tổ hợp khác nhau thì khác nhau về phần tử.
   *Lý thuyết Chỉnh hợp
   – Cho tập hợp A có n phần tử và cho số nguyên k, (1$\le$ k $\le$ n). Khi lấy k phần tử của A và sắp xếp chúng theo một thứ tự, ta được một chỉnh hợp chập k của n phần tử của A (gọi tắt là một chỉnh hợp n chập k của A).
   – Số các chỉnh hợp chập k của một tập hợp có n phần tử là: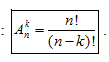 
   – Một số qui ước: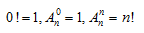 
   *Lý thuyết Tổ hợp
   – Cho tập hợp A có n phần tử và cho số nguyên k, (1$\le$ k $\le$ n). Mỗi tập hợp con của A có phần tử được gọi là một tổ hợp chập k của n phần tử của A.
   – Số các chỉnh hợp chập k của một tập hợp có n phần tử là :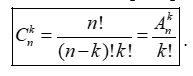 
   –  Một số quy ước: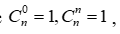 với qui ước này ta có  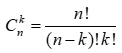đúng với số nguyên dương k, thỏa 0$\le$ k $\le$ n
   PT 14.1. Chọn B
   TH1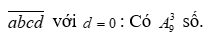 
   TH2: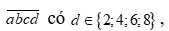 vì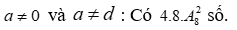 
   Như vậy, có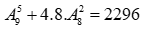  số cần tìm
   PT 14.2.
   Chọn C
   Mỗi tập con có 3 phần tử thuộc tập {1,2,…,9} xác định duy nhất một số có 3 chữ số tăng dần từ trái qua phải (đảm bảo chữ số đầu tiên khác 0).
   Mỗi tập con có 3 phần tử thuộc tập {0,1,2….,9} xác định duy nhất một số có 3 chữ số giảm dần từ trái qua phải.
   Như vậy, có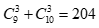  số cần tìm.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Một lớp học có 12 bạn nam và 10  bạn nữ. Số cách chọn hai bạn trực nhật sao cho có cả nam và nữ là  
   
   

   Câu hỏi:
   

   Một lớp học có 12 bạn nam và 10  bạn nữ. Số cách chọn hai bạn trực nhật sao cho có cả nam và nữ là  

   A. 120

   Đáp án chính xác

   B. 231

   C. 210

   D. 22

   Trả lời:

   Chọn A
   Số cách chọn một bạn nam là 12 cách.
   Số cách chọn một bạn nữ là 10 cách
   Vậy số cách chọn hai bạn trực nhật có cả nam và nữ là 12.10 = 120 (cách)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====