Tìm hệ số lớn nhất trong khai triển của: a) (a + b)2022; b) (a + b)2023.

Câu hỏi:

Tìm hệ số lớn nhất trong khai triển của:
a) (a + b)²⁰²²;
b) (a + b)²⁰²³.

Trả lời:

Vì dãy hệ số của khai triển (a + b)ⁿ tăng dần đến “giữa” rồi giảm dần nên:
a) Hệ số lớn nhất của (a + b)²⁰²² là $C_{2022}^{1011}.$
b) Hệ số lớn nhất của (a + b)²⁰²³ là $C_{2023}^{1011} và C_{2023}^{1012}.$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. a) Chọn số thích hợp cho ? trong khai triển biểu thức sau: (a+b)3=C3?a3−?+C3?a3−?b1+C3?a3−?b2+C3?a3−?b3. Từ đó nêu dạng tổng quát của mỗi số hạng trong khai triển biểu thức (a + b)3. b) Xét biểu thức (a + b)n. Nêu dự đoán về dạng tổng quát của mỗi số hạng trong khai triển biểu thức (a + b)n.
   
   

   Câu hỏi:
   

   a) Chọn số thích hợp cho ? trong khai triển biểu thức sau:
   ${(a+b)}^3=C_3^{?}{a}^{3-?}+C_3^{?}{a}^{3-?}{b}^1+C_3^{?}{a}^{3-?}{b}^2+C_3^{?}{a}^{3-?}{b}^3.$

   Từ đó nêu dạng tổng quát của mỗi số hạng trong khai triển biểu thức (a + b)³.
   b) Xét biểu thức (a + b)ⁿ.
   Nêu dự đoán về dạng tổng quát của mỗi số hạng trong khai triển biểu thức (a + b)ⁿ.

   Trả lời:

   a) ${(a+b)}^3=C_3^0{a}^{3-0}+C_3^1{a}^{3-1}{b}^1+C_3^2{a}^{3-2}{b}^2+C_3^3{a}^{3-3}{b}^3.$
   Mỗi số hạng trong khai triển biểu thức (a + b)³ đều có dạng $C_3^k{a}^{3-k}{b}^k.$
   b) Cũng như thế, mỗi số hạng trong khai triển
   biểu thức (a + b)ⁿ đều có dạng $C_n^k{a}^{n-k}{b}^k.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Khai triển biểu thức (x + 2)7.
   
   

   Câu hỏi:
   

   Khai triển biểu thức (x + 2)⁷.

   Trả lời:

   ${\left(x+2\right)}^7=x^7+C_7^1{x}^{6}2+C_7^2{x}^5{2}^2+C_7^3{x}^4{2}^3+C_7^4{x}^3{2}^4+C_7^5{x}^2{2}^5+C_7^{6}x{2}^6+2^7.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho n∈ℕ* . Chứng minh Cn0+Cn1+Cn2+…+Cnn−1+Cnn=2n.
   
   

   Câu hỏi:
   

   Cho $n\in {\mathbb{N}}^{*}$ . Chứng minh $C_n^0+{\text{C}}_n^1+{\text{C}}_n^2+\dots +{\text{C}}_n^{n-1}+{\text{C}}_n^n=2^n.$

   Trả lời:

   Ta có:
   ${\left(x+1\right)}^n=C_n^0{x}^n+C_n^1{x}^{n-1}.1+C_n^2{x}^{n-2}.1^2+\mathrm{\dots }+C_n^{n-1}x.1^{n-1}+C_n^n.1^n=C_n^0{x}^n+C_n^1{x}^{n-1}+C_n^2{x}^{n-2}+\mathrm{\dots }+C_n^{n-1}x+C_n^n.$

   Cho x = 1, ta được:
   ${\left(1+1\right)}^n=C_n^0{1}^n+C_n^1{1}^{n-1}+C_n^2{1}^{n-2}+\mathrm{\dots }+C_n^{n-1}1+C_n^n=C_n^0+{\text{C}}_n^1+{\text{C}}_n^2+\dots +{\text{C}}_n^{n-1}+{\text{C}}_n^n.$
   Vậy $C_n^0+{\text{C}}_n^1+{\text{C}}_n^2+\dots +{\text{C}}_n^{n-1}+{\text{C}}_n^n={\left(1+1\right)}^n=2^n.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Ta đã biết: (a+b)2=C20a2+C21ab+C22b2; (a+b)3=C30a3+C31a2b+C32ab2+C33b3; (a+b)4=C40a4+C41a3b+C42a2b2+C43ab3+C44b4; (a+b)5=C50a5+C51a4b+C52a3b2+C53a2b3+C54ab4+C55b5. Ta sắp xểp những hệ số tổ hợp ở trên như sau: Nêu phép toán để từ hai số hạng của dòng trên suy ra được số hạng tương ứng (thể hiện ở mũi tên ↓) ở dòng dưới trong bảng các hệ số nói trên.
   
   

   Câu hỏi:
   

   Ta đã biết:
   ${(a+b)}^2=C_2^0{a}^2+C_2^{1}ab+C_2^2{b}^2;$
   ${(a+b)}^3=C_3^0{a}^3+C_3^1{a}^{2}b+C_3^{2}a{b}^2+C_3^3{b}^3;$
   ${(a+b)}^4=C_4^0{a}^4+C_4^1{a}^{3}b+C_4^2{a}^2{b}^2+C_4^{3}a{b}^3+C_4^4{b}^4;$
   ${(a+b)}^5=C_5^0{a}^5+C_5^1{a}^{4}b+C_5^2{a}^3{b}^2+C_5^3{a}^2{b}^3+C_5^{4}a{b}^4+C_5^5{b}^5.$

   Ta sắp xểp những hệ số tổ hợp ở trên như sau:
   

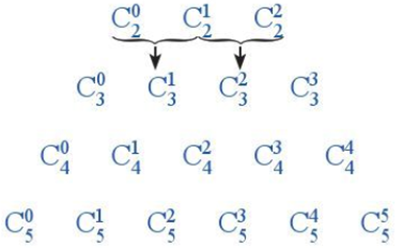
   Nêu phép toán để từ hai số hạng của dòng trên suy ra được số hạng tương ứng (thể hiện ở mũi tên ↓) ở dòng dưới trong bảng các hệ số nói trên.

   Trả lời:

   Tổng của hai số hạng của dòng trên bằng số hạng tương ứng ở dòng dưới.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Sử dụng tam giác Pascal để khai triển: a) (x + y)7; b) (x – 2)7.
   
   

   Câu hỏi:
   

   Sử dụng tam giác Pascal để khai triển:
   a) (x + y)⁷;
   b) (x – 2)⁷.

   Trả lời:

   Tam giác Pascal ứng với n ≤ 7 là:
   

   Vậy:
   a) ${\left(x+y\right)}^7=x^7+7x^{6}y+21x^5{y}^2+35x^4{y}^3+35x^3{y}^4+21x^2{y}^5+7x{y}^6+y^7.$
   b) ${\left(x-2\right)}^7$
   $=x^7+7x^6.\left(-2\right)+21x^5{\left(-2\right)}^2+35x^4{\left(-2\right)}^3+35x^3{\left(-2\right)}^4+21x^2{\left(-2\right)}^5+7x{\left(-2\right)}^6+{\left(-2\right)}^7$
   $=x^7-14x^6+84x^5-280x^4+560x^3-672x^2+448x-128.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====