Tam giác ABC vuông tại B. Trên cạnh AC lấy hai điểm M, N sao cho các góc ABM^, MBN^, NBC^ bằng nhau. Đặt AB = q, BC = m, BM = x, BN = y. Trong các hệ thức sau, hệ thức nào đúng?

Câu hỏi:

Tam giác ABC vuông tại B. Trên cạnh AC lấy hai điểm M, N sao cho các góc $\widehat{ABM},$ $\widehat{MBN},$ $\widehat{NBC}$ bằng nhau. Đặt AB = q, BC = m, BM = x, BN = y. Trong các hệ thức sau, hệ thức nào đúng?

A. AM = MN = NC;

B. AM² = q² + x² – xq;

C. AN² = q² + y² – yq;

Đáp án chính xác

D. AC² = q² + m² – 2qm.

Trả lời:

Hướng dẫn giải
Đáp án đúng là: C

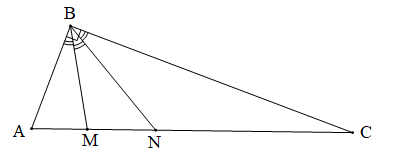
Ta có $\widehat{ABM}=\widehat{MBN}=\widehat{NBC}=\frac{\widehat{ABC}}{3}=\frac{90°}{3}=30°$ 
$\Rightarrow \widehat{ABN}=\widehat{MBC}=60°$ 
Áp dụng định lí côsin cho tam giác ABM ta có:
AM² = AB² + BM² – 2.AB.BM.$cos\widehat{ABM}$ 
Þ AM² = q² + x² – 2.q.x.cos30°
$\Rightarrow A{M}^2=q^2+x^2-2.q.x.\frac{\sqrt{3}}{2}=q^2+x^2-qx\sqrt{3}.$      (1)
Do đó phương án B là mệnh đề sai.
Áp dụng định lí côsin cho tam giác ABN ta có:
AN² = AB² + BN² – 2.AB.BN.$cos\widehat{ABN}$ 
Þ AN² = q² + y² – 2.q.y.cos60°
$\Rightarrow A{N}^2=q^2+y^2-2.q.y.\frac{1}{2}=q^2+y^2-qy.$    (2)
Do đó phương án C là mệnh đề đúng.
Từ (1) và (2) suy ra AM² ≠ AN² nên phương án A là mệnh đề sai.
Tam giác ABC vuông tại B nên AC² = AB² + BC² = q² + m².
Do đó phương án D là mệnh đề sai.
Vậy ta chọn phương án C.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho tam giác ABC, biết BC = 24, AC = 13, AB = 15. Số đo góc A là:
   
   

   Câu hỏi:
   

   Cho tam giác ABC, biết BC = 24, AC = 13, AB = 15. Số đo góc A là:

   A. 28°37′;

   B. 33°34′;

   C. 58°24′;

   D. 117°49′.

   Đáp án chính xác

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: D
   Áp dụng hệ quả định lí côsin cho tam giác ABC ta có:
   $\cos A=\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}=\frac{{15}^2+{13}^2-{24}^2}{\mathrm{2.15.13}}=-\frac{7}{15}$
   Do đó $\widehat{A}\approx 117°49‘.$ 
   Vậy  $\widehat{A}\approx 117°49‘.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tam giác ABC có A^=68°12′,B^=34°44′, AB = 117. Độ dài cạnh AC là khoảng:
   
   

   Câu hỏi:
   

   Tam giác ABC có $\widehat{A}=68°12‘,\widehat{B}=34°44‘,$ AB = 117. Độ dài cạnh AC là khoảng:

   A. 68;

   Đáp án chính xác

   B. 118

   C. 168

   D. 200

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: A
   Xét tam giác ABC có $\widehat{A}=68°12‘,\widehat{B}=34°44‘,$ ta có:
   $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong tam giác)
   $\Rightarrow \widehat{C}=180°-\widehat{A}-\widehat{B}$ 
   $\Rightarrow \widehat{C}=180°-68°12‘-34°44‘=77°4‘.$
   Áp dụng định lí sin trong tam giác ABC ta có: $\frac{AC}{\sin B}=\frac{AB}{\sin C}$
   $\Rightarrow AC=\frac{AB.\sin B}{\sin C}=\frac{117.\sin 34°44‘}{\sin 77°4‘}\approx 68.$ 
   Vậy AC ≈ 68.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tam giác ABC có AB=2;AC=3 và C^=45°. Độ dài cạnh BC là:
   
   

   Câu hỏi:
   

   Tam giác ABC có $AB=\sqrt{2};AC=\sqrt{3}$ và $\widehat{C}=45°$. Độ dài cạnh BC là:

   A. $BC=\frac{\sqrt{6}-\sqrt{2}}{2};$

   B. $BC=\frac{\sqrt{6}+\sqrt{2}}{2};$

   Đáp án chính xác

   C. $\sqrt{5}$

   D. $\sqrt{6}$

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Áp dụng định lí côsin cho tam giác ABC ta có:
   AB² = AC² + BC² – 2.AC.BC.cosC
   $\Rightarrow {\left(\sqrt{2}\right)}^2={\left(\sqrt{3}\right)}^2+B{C}^2-2.\sqrt{3}.BC.cos45°$ 
   $\Rightarrow B{C}^2-\sqrt{6}.BC+1=0$ 
   $\Rightarrow BC=\frac{\sqrt{6}+\sqrt{2}}{2}$ (vì BC > 0)
   Vậy $BC=\frac{\sqrt{6}+\sqrt{2}}{2}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC có AB=3+1,AC=6, BC = 2. Số đo của B^−A^ là:
   
   

   Câu hỏi:
   

   Cho tam giác ABC có $AB=\sqrt{3}+1,AC=\sqrt{6},$ BC = 2. Số đo của $\widehat{B}-\widehat{A}$ là:

   A. 20°;

   B. 25°;

   Đáp án chính xác

   C. 30°;

   D. 35°;

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Áp dụng hệ quả định lí côsin cho tam giác ABC ta có:
   +) $\cos A=\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}=\frac{{\left(\sqrt{3}+1\right)}^2+{\left(\sqrt{6}\right)}^2-2^2}{2.\left(\sqrt{3}+1\right)\sqrt{6}}=\frac{\sqrt{2}}{2}$$\Rightarrow \widehat{A}=45°$ 
   +) $\cos B=\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}=\frac{{\left(\sqrt{3}+1\right)}^2+2^2-{\left(\sqrt{6}\right)}^2}{2.\left(\sqrt{3}+1\right).2}=\frac{1}{2}$$\Rightarrow \widehat{B}=60°$ 
   Do đó $\widehat{B}-\widehat{A}=60°-45°=25°.\Rightarrow \widehat{B}=60°$ 
   Vậy  $\widehat{B}-\widehat{A}=25°.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tam giác ABC có góc A nhọn, AB = 5, AC = 8, diện tích bằng 12. Độ dài cạnh BC là khoảng:
   
   

   Câu hỏi:
   

   Tam giác ABC có góc A nhọn, AB = 5, AC = 8, diện tích bằng 12. Độ dài cạnh BC là khoảng:

   A. $2\sqrt{3}$

   B. $3\sqrt{2}$

   C. 4

   D. 5

   Đáp án chính xác

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: D
   Diện tích tam giác ABC là: $S=\frac{1}{2}.AB.AC.\sin A\Rightarrow \sin A=\frac{2S}{AB.AC}$
   $\Rightarrow \sin A=\frac{2.12}{5.8}=\frac{3}{5}\Rightarrow \widehat{A}\approx 36°52‘$  (vì góc A là góc nhọn)
   Xét tam giác ABC có AB = 5, AC = 8 và $\widehat{A}\approx 36°52‘$, áp dụng định lí côsin ta có:
   BC² = AB² + AC² – 2.AB.AC.cosA
   BC² ≈ 5² + 8² – 2.5.8.cos36°52′ ≈ 25
   Þ BC ≈ 5.
   Vậy BC ≈ 5.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====