Câu hỏi:
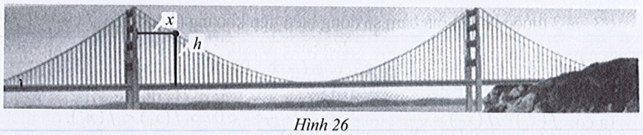
Quan sát chiếc Cổng Vàng (Golden Gate bridge) ở Hình 26. Độ cao h (feet) tính từ mặt cầu đến các điểm trên dây treo ở phần giữa hai trụ cầu được xác định bởi công thức h(x) = \(\frac{1}{{9\,\,000}}{x^2} – \frac{7}{{15}}x + 500\), trong đó x(feet) là khoảng cách từ trụ cầu bên trái đến điểm tương ứng trên dây treo.
Xác định độ cao của trụ cầu so với mặt cầu theo đơn vị feet.
Trả lời:
Lời giải
Đặt hệ trục như hình vẽ dưới đây:
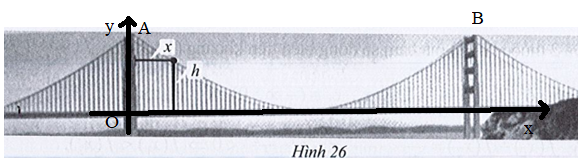
Độ cao của trụ cầu bên trái chính là tung độ của điểm giao giữa trụ cầu (trục tung) và dây treo (parabol) là điểm A.
Thay x = 0 vào h(x) = \(\frac{1}{{9\,\,000}}{x^2} – \frac{7}{{15}}x + 500\), ta được h(0) = \(\frac{1}{{9\,\,000}}{.0^2} – \frac{7}{{15}}.0 + 500\) = 500.
Vậy chiều cao của trụ cầu bên trái là 500 (feet).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các hàm số sau, hàm số nào không là hàm số bậc hai?
A. y = – 5×2 + 6x;
B. y = 3 – 2×2;
C. y = – x(5x – 7);
D. y = 0x2 + 6x – 5.
Câu hỏi:
Trong các hàm số sau, hàm số nào không là hàm số bậc hai?
A. y = – 5x2 + 6x;
B. y = 3 – 2x2;
C. y = – x(5x – 7);
D. y = 0x2 + 6x – 5.Trả lời:
Lời giải
Đáp án đúng là D
Xét hàm số y = – 5x2 + 6x có dạng ax2 + bx + c với a = – 5, b = 6 và c = 0. Do đó A sai.
Xét hàm số y = 3 – 2x2 = – 2x2 + 3 có dạng ax2 + bx + c với a = – 2, b = 0 và c = 3. Do đó B sai.
Xét hàm số y = – x(5x – 7) = – 5x2 + 7x có dạng ax2 + bx + c với a = – 5, b = 7 và c = 0. Do đó C sai.
Xét hàm số y = 0x2 + 6x – 5 có dạng ax2 + bx + c tuy nhiên a = 0 nên đây không là hàm số bậc hai. Do đó D đúng.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập nghiệm của bất phương trình – 5×2 + 6x + 11 ≤ 0 là:
A. \(\left[ { – 1;\frac{{11}}{5}} \right]\);
B. \(\left( { – 1;\frac{{11}}{5}} \right)\);
C. \(\left( { – \infty ; – 1} \right) \cup \left( {\frac{{11}}{5}; + \infty } \right)\);
D. \(\left( { – \infty ; – 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\).
Câu hỏi:
Tập nghiệm của bất phương trình – 5x2 + 6x + 11 ≤ 0 là:
A. \(\left[ { – 1;\frac{{11}}{5}} \right]\);
B. \(\left( { – 1;\frac{{11}}{5}} \right)\);
C. \(\left( { – \infty ; – 1} \right) \cup \left( {\frac{{11}}{5}; + \infty } \right)\);
D. \(\left( { – \infty ; – 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\).Trả lời:
Lời giải
Đáp án đúng là D
Xét tam thức bậc hai f(x) = – 5x2 + 6x + 11 với a = – 5, ∆ = 62 – 4.(– 5).11 = 256 > 0.
Suy ra tam thức f(x) có hai nghiệm phân biệt x1 = – 1 và x2 = \(\frac{{11}}{5}\).
Áp dụng định lí về dấu của tam thức bậc hai, ta có: f(x) < 0 khi x ∈ \(\left( { – \infty ; – 1} \right) \cup \left( {\frac{{11}}{5}; + \infty } \right)\).
Do đó bất phương trình – 5x2 + 6x + 11 ≤ 0 khi x ∈ \(\left( { – \infty ; – 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\).
Vậy tập nghiệm của bất phương trình là S = \(\left( { – \infty ; – 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số f(x) = \(\left\{ \begin{array}{l}1\,\,\,khi\,\,x < 0\\2\,\,khi\,x > 0\end{array} \right.\).
Điểm nào sau đây thuộc đồ thị hàm số trên:
A(0; 0), B(– 1; 1), C(2 021; 1), D(2 022; 2)?
Câu hỏi:
Cho hàm số f(x) = \(\left\{ \begin{array}{l}1\,\,\,khi\,\,x < 0\\2\,\,khi\,x > 0\end{array} \right.\).
Điểm nào sau đây thuộc đồ thị hàm số trên:
A(0; 0), B(– 1; 1), C(2 021; 1), D(2 022; 2)?Trả lời:
Lời giải
Tập xác định của hàm số đã cho là D = ℝ\{0}.
+) Điểm A(0; 0) có x = 0 không thỏa mãn điều kiện xác định nên không thuộc đồ thị hàm số.
+) Điểm B(– 1; 1) có x = – 1 và y = 1
Vì x = – 1 < 0 nên y = f(x) = 1 (thỏa mãn). Do đó điểm B thuộc đồ thị hàm số đã cho.
+) Điểm C(2 021; 1) có x = 2 021 và y = 1
Vì x = 2 021 > 0 nên y = f(x) = 2 ≠ 1. Do đó điểm C không thuộc đồ thị hàm số đã cho.
+) Điểm D(2 022; 2) có x = 2 022 và y = 2
Vì x = 2 022 > 0 nên y = f(x) = 2 (thỏa mãn). Do đó điểm D thuộc đồ thị hàm số đã cho.
Vậy có điểm B và điểm D thuộc đồ thị hàm số đã cho.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Chỉ ra hai điểm thuộc đồ thị hàm số trên có tung độ bằng 2.
Câu hỏi:
Chỉ ra hai điểm thuộc đồ thị hàm số trên có tung độ bằng 2.
Trả lời:
Lời giải
Để điểm có tung độ bằng 2 thì hoành độ của điểm đó phải thỏa mãn x > 0. Do đó ta chọn được được 2 điểm là (100; 2) và (67; 2).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Chỉ ra điểm thuộc đồ thị hàm số trên có hoành độ bằng – 2 022.
Câu hỏi:
Chỉ ra điểm thuộc đồ thị hàm số trên có hoành độ bằng – 2 022.
Trả lời:
Lời giải
Điểm có hoành độ x = – 2 022 < 0 nên tung độ y = 1. Do đó ta có điểm cần tìm là (– 2 022; 1).====== **** mời các bạn xem câu tiếp bên dưới **** =====