Cho hàm số f(x) = \(\left\{ \begin{array}{l}1\,\,\,khi\,\,x < 0\\2\,\,khi\,x > 0\end{array} \right.\). Điểm nào sau đây thuộc đồ thị hàm số trên: A(0; 0), B(– 1; 1), C(2 021; 1), D(2 022; 2)?

Câu hỏi:

Cho hàm số f(x) = \(\left\{ \begin{array}{l}1\,\,\,khi\,\,x < 0\\2\,\,khi\,x > 0\end{array} \right.\).
Điểm nào sau đây thuộc đồ thị hàm số trên:
A(0; 0), B(– 1; 1), C(2 021; 1), D(2 022; 2)?

Trả lời:

Lời giải
Tập xác định của hàm số đã cho là D = ℝ\{0}.
+) Điểm A(0; 0) có x = 0 không thỏa mãn điều kiện xác định nên không thuộc đồ thị hàm số.
+) Điểm B(– 1; 1) có x = – 1 và y = 1
Vì x = – 1 < 0 nên y = f(x) = 1 (thỏa mãn). Do đó điểm B thuộc đồ thị hàm số đã cho.
+) Điểm C(2 021; 1) có x = 2 021 và y = 1
Vì x = 2 021 > 0 nên y = f(x) = 2 ≠ 1. Do đó điểm C không thuộc đồ thị hàm số đã cho.
+) Điểm D(2 022; 2) có x = 2 022 và y = 2
Vì x = 2 022 > 0 nên y = f(x) = 2 (thỏa mãn). Do đó điểm D thuộc đồ thị hàm số đã cho.
Vậy có điểm B và điểm D thuộc đồ thị hàm số đã cho.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong các hàm số sau, hàm số nào không là hàm số bậc hai? A. y = – 5×2 + 6x; B. y = 3 – 2×2; C. y = – x(5x – 7); D. y = 0x2 + 6x – 5.
   
   

   Câu hỏi:
   

   Trong các hàm số sau, hàm số nào không là hàm số bậc hai?
   A. y = – 5x² + 6x;
   B. y = 3 – 2x²;
   C. y = – x(5x – 7);
   D. y = 0x² + 6x – 5.

   Trả lời:

   Lời giải
   Đáp án đúng là D
   Xét hàm số y = – 5x² + 6x có dạng ax² + bx + c với a = – 5, b = 6 và c = 0. Do đó A sai.
   Xét hàm số y = 3 – 2x² = – 2x² + 3 có dạng ax² + bx + c với a = – 2, b = 0 và c = 3. Do đó B sai.
   Xét hàm số y = – x(5x – 7) = – 5x² + 7x có dạng ax² + bx + c với a = – 5, b = 7 và c = 0. Do đó C sai.
   Xét hàm số y = 0x² + 6x – 5 có dạng ax² + bx + c tuy nhiên a = 0 nên đây không là hàm số bậc hai. Do đó D đúng.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tập nghiệm của bất phương trình – 5×2 + 6x + 11 ≤ 0 là: A. \(\left[ { – 1;\frac{{11}}{5}} \right]\); B. \(\left( { – 1;\frac{{11}}{5}} \right)\); C. \(\left( { – \infty ; – 1} \right) \cup \left( {\frac{{11}}{5}; + \infty } \right)\); D. \(\left( { – \infty ; – 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\).
   
   

   Câu hỏi:
   

   Tập nghiệm của bất phương trình – 5x² + 6x + 11 ≤ 0 là:
   A. \(\left[ { – 1;\frac{{11}}{5}} \right]\);
   B. \(\left( { – 1;\frac{{11}}{5}} \right)\);
   C. \(\left( { – \infty ; – 1} \right) \cup \left( {\frac{{11}}{5}; + \infty } \right)\);
   D. \(\left( { – \infty ; – 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\).

   Trả lời:

   Lời giải
   Đáp án đúng là D
   Xét tam thức bậc hai f(x) = – 5x² + 6x + 11 với a = – 5, ∆ = 6² – 4.(– 5).11 = 256 > 0.
   Suy ra tam thức f(x) có hai nghiệm phân biệt x₁ = – 1 và x₂ = \(\frac{{11}}{5}\).
   Áp dụng định lí về dấu của tam thức bậc hai, ta có: f(x) < 0 khi x ∈ \(\left( { – \infty ; – 1} \right) \cup \left( {\frac{{11}}{5}; + \infty } \right)\).
   Do đó bất phương trình – 5x² + 6x + 11 ≤ 0 khi x ∈ \(\left( { – \infty ; – 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\).
   Vậy tập nghiệm của bất phương trình là S = \(\left( { – \infty ; – 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Chỉ ra hai điểm thuộc đồ thị hàm số trên có tung độ bằng 2.
   
   

   Câu hỏi:
   

   Chỉ ra hai điểm thuộc đồ thị hàm số trên có tung độ bằng 2.

   Trả lời:

   Lời giải
   Để điểm có tung độ bằng 2 thì hoành độ của điểm đó phải thỏa mãn x > 0. Do đó ta chọn được được 2 điểm là (100; 2) và (67; 2).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Chỉ ra điểm thuộc đồ thị hàm số trên có hoành độ bằng – 2 022.
   
   

   Câu hỏi:
   

   Chỉ ra điểm thuộc đồ thị hàm số trên có hoành độ bằng – 2 022.

   Trả lời:

   Lời giải
   Điểm có hoành độ x = – 2 022 < 0 nên tung độ y = 1. Do đó ta có điểm cần tìm là (– 2 022; 1).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số y = f(x) có đồ thị ở Hình 24. Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).
   
   

   Câu hỏi:
   

   Cho hàm số y = f(x) có đồ thị ở Hình 24.
   
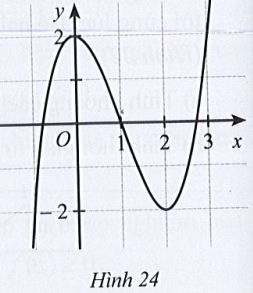
   Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).

   Trả lời:

   Lời giải
   Dựa vào đồ thị hàm số ta thấy:
   Với x < 0 hoặc x > 2 thì đồ thị hàm số đi lên. Do đó hàm số đồng biến trên khoảng (– ∞; 0) ∪ (2; +∞).
   Với 0 < x < 2 thì đồ thị hàm số đi xuống. Do đó hàm số nghịch biến trên khoảng (0; 2).
   Vậy hàm số đồng biến trên khoảng (– ∞; 0) ∪ (2; +∞) và hàm số nghịch biến trên khoảng (0; 2).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====