Một hình chữ nhật có chu vi bằng 20 cm. Để điện tích hình chữ nhật lớn hơn hoặc bằng 15 cm2 thì chiều rộng của hình chữ nhật nằm trong khoảng bao nhiêu?

Câu hỏi:

Một hình chữ nhật có chu vi bằng 20 cm. Để điện tích hình chữ nhật lớn hơn hoặc bằng 15 cm² thì chiều rộng của hình chữ nhật nằm trong khoảng bao nhiêu?

Trả lời:

Gọi x (cm) là chiều rộng hình chữ nhật.
Khi đó chiều dài hình chữ nhật là $\frac{20}{2}$  – x hay 10 – x (cm)
Chiều dài và chiều rộng của hình chữ nhật đều lớn hơn 0 và chiều rộng nhỏ hơn hoặc bằng chiều dài, ta có: 0 < x ≤ 10 – x hay 0 < x ≤ 5 (cm) (1)
Diện tích của hình chữ nhật là S = x. ( 10 – x )
Ta có x.( 10 – x ) ≥ 15 khi và chỉ khi x² + 10x – 15 ≥ 0.
Tam thức bậc hai f ( x ) = x² + 10x – 15 có ∆ = 10² – 4.1.(– 15) = 160 > 0 hai nghiệm phân biệt x₁ = –5 + 2 $\sqrt{10}$ và x₂ = –5 – 2 $\sqrt{10}$ , a = 1 > 0 nên f ( x ) ≥ 0 khi và chỉ khi x ≤ –5 – 2 $\sqrt{10}$ hoặc x ≥ –5 + 2 $\sqrt{10}$.
Kết hợp với điều kiện (1) ta được –5 + 2 $\sqrt{10}$ ≤ x ≤ 5 hay 1,33 ≤ x ≤ 5.
Vậy chiều rộng của hình chữ nhật nằm trong khoảng từ 1,33 cm đến 5 cm thì thỏa mãn yêu cầu bài toán.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. x = 2 là một nghiệm của bất phương trình nào sau đây? a) x2−3x+1>0;
   
   

   Câu hỏi:
   

   x = 2 là một nghiệm của bất phương trình nào sau đây?
   a) $x^2-3x+1>0;$

   Trả lời:

   a) Thay x = 2 vào bất phương trình ta được: 2² – 3.2 +1 = –1 < 0.
   Vì vậy x = 2 không là nghiệm của bất phương trình $x^2-3x+1>0$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. b) −4×2−3x+5≤0;
   
   

   Câu hỏi:
   

   b) $-4x^2-3x+5\le 0;$

   Trả lời:

   b) Thay x = 2 vào bất phương trình ta được: –4.2² – 3.2 +5 = –17 < 0.
   Vì vậy x = 2 là nghiệm của bất phương trình $-4x^2-3x+5\le 0$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. c) 2×2−5x+2≤0
   
   

   Câu hỏi:
   

   c) $2x^2-5x+2\le 0$

   Trả lời:

   c) Thay x = 2 vào bất phương trình ta được: 2.2² – 5.2 + 2 = 0 ≤ 0
   Vì vậy x = 2 là nghiệm của bất phương trình $2x^2-5x+2\le 0$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Dựa vào đồ thị của hàm số bậc hai đã cho, hãy nêu tập nghiệm của các bất phương trình bậc hai tương ứng. a) fx≥0
   
   

   Câu hỏi:
   

   Dựa vào đồ thị của hàm số bậc hai đã cho, hãy nêu tập nghiệm của các bất phương trình bậc hai tương ứng.
   a) $f\left(x\right)\ge 0$
   

   Trả lời:

   a) $\left[-\frac{5}{2};1\right]$
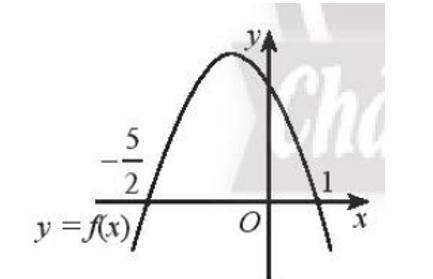
   Đồ thị hàm số bậc hai nằm phía trên trục hoành với $x\in \left(-\frac{5}{2};1\right)$ ;
   Đồ thị hàm số bậc hai cắt trục hoành tại hai điểm x = $-\frac{5}{2}$  và x = 1.
   Do đó f(x) ≥ 0 khi $\left[-\frac{5}{2};1\right]$ .
   Vậy tập nghiệm của bất phương trình f(x) ≥ 0 là S = $\left[-\frac{5}{2};1\right]$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. b) fx&lt;0
   
   

   Câu hỏi:
   

   b) $f\left(x\right)<0$
   

   Trả lời:

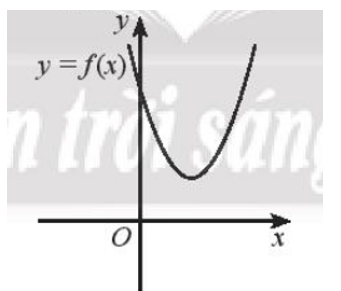
   b) Đồ thị hàm số bậc hai nằm phía trên trục hoành với mọi x ∈ ℝ hay f(x) > 0 với mọi x ∈ ℝ.
   Do đó f(x) < 0 vô nghiệm.
   Vậy tập nghiệm của bất phương trình f(x) < 0 là S = ∅.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====