Câu hỏi:
Lớp 10A có 45 học sinh, trong đó có 15 học sinh được xếp loại học lực giỏi, 20 học sinh được xếp loại hạnh kiểm tốt, 10 em vừa xếp loại học lực giỏi, vừa có hạnh kiểm tốt. Hỏi có bao nhiêu học sinh xếp loại học lực giỏi hoặc có hạnh kiểm tốt?
A. 25;
Đáp án chính xác
B. 10;
C. 45;
D. 35.
Trả lời:
Đáp án đúng là: A
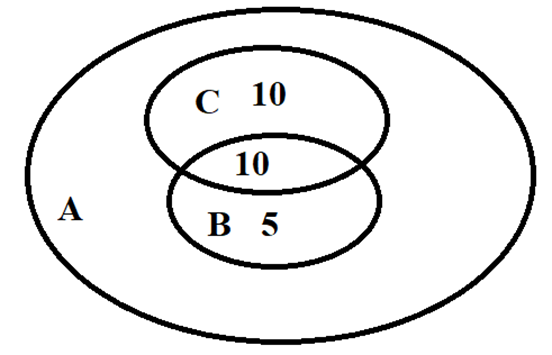
Gọi A là tập hợp học sinh lớp 10A; B là tập học sinh được xếp loại học lực giỏi; C là tập học sinh được xếp loại hạnh kiểm tốt. Khi đó tập hợp cần tìm là tập \({\rm{B}} \cup {\rm{C}}\). Tập này có 25 học sinh. Được thể hiện trong biểu đồ Ven như sau:
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số tập con của tập A = {1; 2; 3} là
Câu hỏi:
Số tập con của tập A = {1; 2; 3} là
A. 8;
Đáp án chính xác
B. 6;
C. 5;
D. 7.
Trả lời:
Đáp án đúng là: A
Các tập con gồm {1}; {2}; {3}; {1; 2}; {1;3}; {2; 3}; {1; 2; 3}; \(\emptyset \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hãy liệt kê các phần tử của tập hợp \(X = \,{\rm{\{ }}x \in \mathbb{R},\,{x^2} + x + 1 = 0\} \)
Câu hỏi:
Hãy liệt kê các phần tử của tập hợp \(X = \,{\rm{\{ }}x \in \mathbb{R},\,{x^2} + x + 1 = 0\} \)
A. X = \(\emptyset \);
Đáp án chính xác
B. X = {0};
C. X = 0;
D. X = {\(\emptyset \)}.
Trả lời:
Đáp án đúng là: A
Phương trình x2 + x + 1 = 0 vô nghiệm nên tập X không có phần tử nào.
Vậy tập X = \(\emptyset \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số tập con có 2 phần tử của tập M = {1; 2; 3; 4; 5; 6}
Câu hỏi:
Số tập con có 2 phần tử của tập M = {1; 2; 3; 4; 5; 6}
A. 15;
Đáp án chính xác
B. 16;
C. 18;
D. 22.
Trả lời:
Đáp án đúng là: A
Tập con có 2 phần tử của tập M gồm: {1; 2}; {1; 3}; {1; 4}; {1; 5}; {1;6}; {2; 3}; {2; 4}; {2; 5}; {2; 6}; {3; 4}; {3; 5}; {3; 6}; {4; 5}; {4; 6}; {5; 6}.
Vậy tập M có 15 tập con có 2 phần tử.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai tập hợp A = {0; 2; 3; 5} và B = {2; 7}. Khi đó \({\rm{A}} \cap {\rm{B}}\)
Câu hỏi:
Cho hai tập hợp A = {0; 2; 3; 5} và B = {2; 7}. Khi đó \({\rm{A}} \cap {\rm{B}}\)
A. {2; 5};
B. {2};
Đáp án chính xác
C. \(\emptyset \);
D. {0; 2; 3; 5; 7}.
Trả lời:
Đáp án đúng là: B
Vì phần tử 2 vừa thuộc A vừa thuộc B nên \({\rm{A}} \cap {\rm{B}} = \left\{ 2 \right\}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho A = {0; 1; 2; 3; 4}; B = {2; 3; 4; 5; 6}. Tìm tập \(\left( {{\rm{A}}\backslash {\rm{B}}} \right) \cup \left( {{\rm{B}}\backslash {\rm{A}}} \right)\)
Câu hỏi:
Cho A = {0; 1; 2; 3; 4}; B = {2; 3; 4; 5; 6}. Tìm tập \(\left( {{\rm{A}}\backslash {\rm{B}}} \right) \cup \left( {{\rm{B}}\backslash {\rm{A}}} \right)\)
A. {5; 6};
B. {1; 2};
C. {2; 3; 4};
D. {0; 1; 5; 6}.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Ta có tập hợp A\B là tập các phần tử thuộc tập A nhưng không thuộc tập B nên \(\left( {{\rm{A}}\backslash {\rm{B}}} \right) = {\rm{\{ 0;}}\,{\rm{1\} }}\).
Tập hợp B\A là tập các phần tử thuộc tập B nhưng không thuộc tập A nên \(\left( {{\rm{B}}\backslash {\rm{A}}} \right) = {\rm{\{ }}5;\,6\} \).
\( \Rightarrow \left( {{\rm{A}}\backslash {\rm{B}}} \right) \cup \left( {{\rm{B}}\backslash {\rm{A}}} \right) = \left\{ {0;\,1;\,5;\,6} \right\}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====