Lập bảng biến thiên của hàm số y = x2 + 2x + 3. Hàm số này có giá trị lớn nhất hay nhỏ nhất? Tìm giá trị đó.

Câu hỏi:

Lập bảng biến thiên của hàm số y = x² + 2x + 3. Hàm số này có giá trị lớn nhất hay nhỏ nhất? Tìm giá trị đó.

Trả lời:

Xét hàm số bậc hai: y = x² + 2x + 3 có a = 1, b = 2 và c = 3.
Đỉnh S có tọa độ x_s = $\frac{-b}{2a}=\frac{-2}{2.1}=-1$, y_s = (-1)² + 2.(-1) + 3 = 2. Hay S(-1; 2).
Vì hàm số bậc hai có a = 1 > 0 nên ta có bảng biến thiên sau:

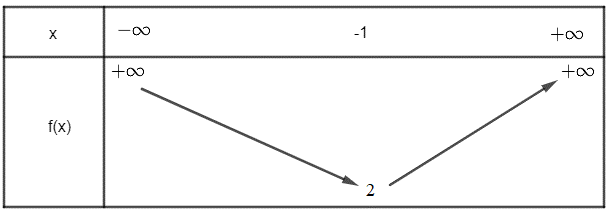
Hàm số có giá trị nhỏ nhất bằng 2 khi x = -1.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Các hàm số này có chung đặc điểm gì? y = ax2; y = a(x – m)(x – n); y = ax2 + bx; y = a(x – h)2 + k; y = ax2 + bx + c.
   
   

   Câu hỏi:
   

   Các hàm số này có chung đặc điểm gì?
   y = ax²;
   y = a(x – m)(x – n);
   y = ax² + bx;
   y = a(x – h)² + k;
   y = ax² + bx + c.

   Trả lời:

   Ta có:
   y = a(x – m)(x – n) = ax² – a(m + n)x + a.m.n.
   y = a(x – h)² + k = ax² – 2ahx + ah² + k.
   Các hàm số đã cho đều là các hàm số bậc hai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai? a) y = 2x(x – 3); b) y = x(x2 + 2) – 5; c) y = -5(x + 1)(x – 4).
   
   

   Câu hỏi:
   

   Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai?
   a) y = 2x(x – 3);
   b) y = x(x² + 2) – 5;
   c) y = -5(x + 1)(x – 4).

   Trả lời:

   a) Xét hàm số: y = 2x(x – 3) = 2x² – 6x.
   Bậc cao nhất của hàm số là bậc hai.
   b) Xét hàm số: y = x(x² + 2) – 5 = x³ + 2x – 5.
   Bậc cao nhất của hàm số là bậc ba.
   c) y = -5(x + 1)(x – 4) = – 5x²  + 15x + 20.
   Bậc cao nhất của hàm số là bậc hai.
   Vậy hàm số ở ý a) và c) là các số có lũy thừa bậc cao nhất của x là bậc hai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hàm số nào trong các hàm số đã cho ở hoạt động khám phá 1 là hàm số bậc hai?
   
   

   Câu hỏi:
   

   Hàm số nào trong các hàm số đã cho ở hoạt động khám phá 1 là hàm số bậc hai?

   Trả lời:

   Các hàm số ở hoạt động khám phá 1:
   a) y = 2x(x – 3) = 2x² – 6x là hàm số bậc hai với a = 2, b = – 6, c = 0.
   b) y = x(x² + 2) – 5 = x³ + 2x – 5 không là hàm số bậc hai
   c) y = -5(x + 1)(x – 4) = – 5x²  + 15x + 20 là hàm số bậc hai với a = -5, b = 15, c = 20.
   Vậy hàm số ở ý a) và c) là các hàm số bậc hai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
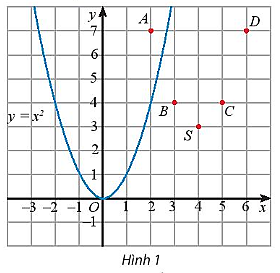
4. a) Xét hàm số: y = f(x) = x2 – 8x + 19 = (x – 4)2 + 3 có bảng giá trị: x 2 3 4 5 6 f(x) 7 4 3 4 7 Trên mặt phẳng tọa độ, ta có các điểm (x; f(x)) với x thuộc bảng giá trị đã cho (Hình 1). Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị của hàm số y = x2 trên Hình 1. b) Tương tự, xét hàm số: y = g(x) = – x2 + 8x – 13 = – (x – 4)2 + 3 có bảng giá trị: x 2 3 4 5 6 g(x) -1 2 3 2 -1 Trên mặt phẳng tọa độ, ta có các điểm (x; g(x)) với x thuộc bảng giá trị đã cho (Hình 2). Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số y = – x2 trên Hình 2.
   
   

   Câu hỏi:
   

   a) Xét hàm số: y = f(x) = x² – 8x + 19 = (x – 4)² + 3 có bảng giá trị:

   x

   2

   3

   4

   5

   6

   f(x)

   7

   4

   3

   4

   7

   Trên mặt phẳng tọa độ, ta có các điểm (x; f(x)) với x thuộc bảng giá trị đã cho (Hình 1).
   Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị của hàm số y = x² trên Hình 1.
   

   b) Tương tự, xét hàm số: y = g(x) = – x² + 8x – 13 = – (x – 4)² + 3 có bảng giá trị:

   x

   2

   3

   4

   5

   6

   g(x)

   -1

   2

   3

   2

   -1

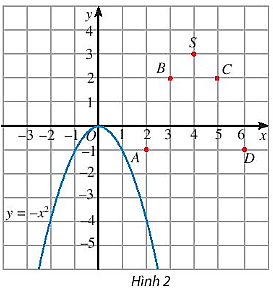
   Trên mặt phẳng tọa độ, ta có các điểm (x; g(x)) với x thuộc bảng giá trị đã cho (Hình 2).
   Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số y = – x² trên Hình 2.
   

   Trả lời:

   a) Đường cong đi qua các điểm A, B, S, C, D là đường cong màu đỏ trên hình vẽ:
   

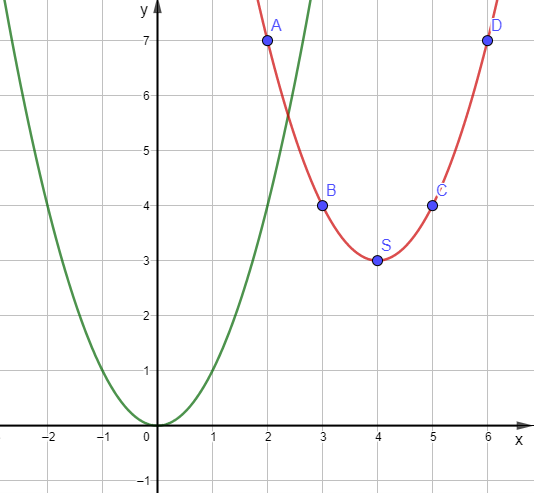
   Nhận xét:
   Về hình dáng của đường cong màu đỏ giống với hình dáng của đường cong màu xanh là một đường cong parabol.
   – Có đỉnh là điểm S với hoành độ là 4 và tung độ là 3.
   – Có trục đối xứng là đường thẳng x = 4 (đường thẳng này đi qua đỉnh S và song song với trục Oy).
   – Bề lõm của đồ thị hướng lên trên.
   b) ) Đường cong đi qua các điểm A, B, S, C, D là đường cong màu cam trên hình vẽ:
   

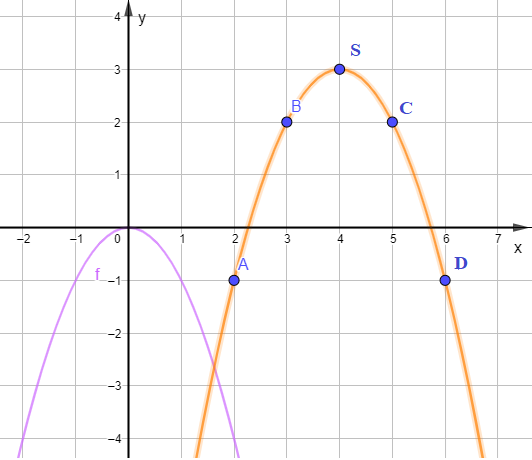
   Nhận xét:
   Về hình dáng của đường cong màu cam giống với hình dáng của đường cong màu tím là một đường cong parabol.
   – Có đỉnh là điểm S với hoành độ là 4 và tung độ là 3.
   – Có trục đối xứng là đường thẳng x = 4 (đường thẳng này đi qua đỉnh S và song song với trục Oy).
   – Bề lõm của đồ thị hướng xuống dưới.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Vẽ đồ thị hàm số y = x2 – 4x + 3 rồi so sánh đồ thị hàm số này với đồ thị hàm số ở ví dụ 2a. Nếu nhận xét về hai đồ thị này.
   
   

   Câu hỏi:
   

   Vẽ đồ thị hàm số y = x² – 4x + 3 rồi so sánh đồ thị hàm số này với đồ thị hàm số ở ví dụ 2a. Nếu nhận xét về hai đồ thị này.

   Trả lời:

   Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x² – 4x + 3 là một parabol (P):
   – Có đỉnh S với hoàng độ x_S = 2, tung độ y_S = -1;
   – Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
   – Bề lõm quay lên trên vì a = 1 > 0;
   – Cắt trục tung tại điểm có tung độ y = 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
   

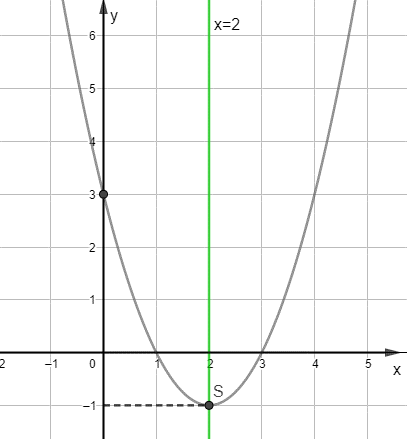
   So với đồ thị của hàm số ở ví dụ 2 a) ta thấy:
   – Hai đồ thị đều là đường cong parabol.
   – Hai đồ thị có cùng trục đối xứng x = 2.
   – Đồ thị ở ví dụ 2a) có bề lõm hướng xuống dưới, còn đồ thị hàm số này có bề lõm hướng lên trên.
   – Hai tọa độ đỉnh của hai đồ thị hàm số đối xứng qua trục Ox.
   – Giao điểm của đồ thị hàm số ở ví dụ 2a) với trục tung đối xứng với giao điểm của đồ thị hàm số này với trục tung.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====