Giả sử hàm số bậc hai mô phỏng vòm phía trong một trụ của cầu Nhật Tân là y = f(x) = \( – \frac{{187}}{{856}}{x^2} + \frac{{8041}}{{856}}x\) (đơn vị đo: mét). Hãy tính chiều dài đoạn dây dọi sử dụng nếu khoảng cách từ chân của trụ cầu đến quả nặng là 30 cm.

Câu hỏi:

Giả sử hàm số bậc hai mô phỏng vòm phía trong một trụ của cầu Nhật Tân là
y = f(x) = \( – \frac{{187}}{{856}}{x^2} + \frac{{8041}}{{856}}x\) (đơn vị đo: mét).
Hãy tính chiều dài đoạn dây dọi sử dụng nếu khoảng cách từ chân của trụ cầu đến quả nặng là 30 cm.

Trả lời:

Hướng dẫn giải
Từ Bài 4 phần Bài tập mẫu, ta có đồ thị hàm số y = f(x) = \( – \frac{{187}}{{856}}{x^2} + \frac{{8041}}{{856}}x\) như hình sau:

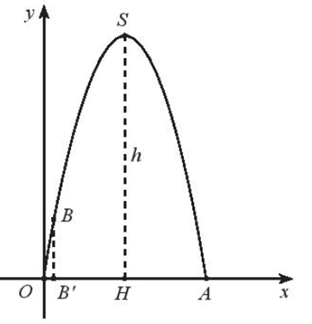
Ta xét điểm B trên hình.
Đổi 30 cm = 0,3 m.
Chiều dài l của đoạn dây dọi sử dụng là tung độ của điểm B trên parabol có x_B = 0,3.
Nên ta có: l = BB’ = f(0,3) = \( – \frac{{187}}{{856}}.{\left( {0,3} \right)^2} + \frac{{8041}}{{856}}.0,3 \approx 2,8\) (m).
Vậy chiều dài dây dọi khoảng 2,8 m.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Hàm số nào trong các hàm sau đây không phải là hàm số bậc hai? a) y = 3×2 + x – \(\sqrt 3 \); b) y = x2 + |x + 1|; c) \(y = \left\{ \begin{array}{l}{x^2} + 1\,\,\,\,\,\,\,\,\,khi\,\,x \ge 0\\ – 2{x^2} – x\,\,khi\,x < 0;\end{array} \right.\) d) y = 2(x2 + 1) + 3x – 1.
   
   

   Câu hỏi:
   

   Hàm số nào trong các hàm sau đây không phải là hàm số bậc hai?

   a) y = 3x² + x – \(\sqrt 3 \);
   b) y = x² + |x + 1|;
   c) \(y = \left\{ \begin{array}{l}{x^2} + 1\,\,\,\,\,\,\,\,\,khi\,\,x \ge 0\\ – 2{x^2} – x\,\,khi\,x < 0;\end{array} \right.\)
   d) y = 2(x² + 1) + 3x – 1.

   Trả lời:

   Hướng dẫn giải
   + Hàm số a) có dạng y = ax² + bx + c với a = 3 ≠ 0, b = 1 và c = \( – \sqrt 3 \) nên đây là hàm số bậc hai.
   + Hàm số b) không phải là hàm số bậc hai vì công thức của hàm số có chứa dấu giá trị tuyệt đối.
   + Hàm số c) không phải là hàm số bậc hai vì hàm số này được cho bởi hai công thức.
   + Ta có y = 2(x² + 1) + 3x – 1 hay y = 2x² + 3x + 1 nên hàm số d) là hàm số bậc hai vì nó có dạng y = ax² + bx + c với a = 2 ≠ 0, b = 3 và c = 1.
   Vậy trong các hàm số đã cho, hàm số b) và hàm số c) không phải là hàm số bậc hai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số bậc hai có đồ thị là parabol có đỉnh S, đi qua các điểm A, B, C(0; – 1) được cho trong Hình 10. Vẽ đồ thị hàm số đã cho;
   
   

   Câu hỏi:
   

   Cho hàm số bậc hai có đồ thị là parabol có đỉnh S, đi qua các điểm A, B, C(0; – 1) được cho trong Hình 10.
   
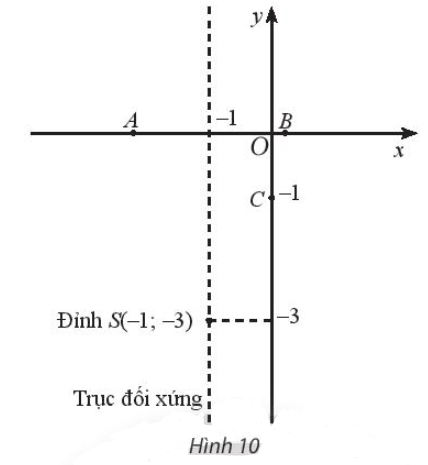
   Vẽ đồ thị hàm số đã cho;

   Trả lời:

   Hướng dẫn giải
   Ta vẽ parabol có bề lõm hướng lên trên và đi qua các điểm A, S, C, B, ta được đồ thị của hàm số đã cho như sau:
   

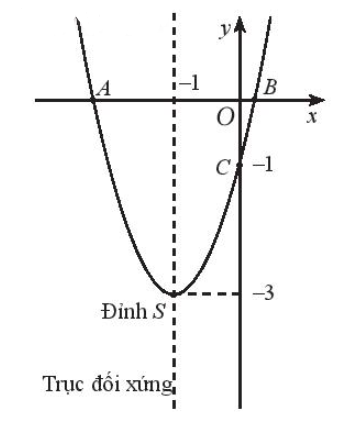
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tìm tập giá trị của hàm số và chỉ ra các khoảng biến thiên của hàm số.
   
   

   Câu hỏi:
   

   Tìm tập giá trị của hàm số và chỉ ra các khoảng biến thiên của hàm số.

   Trả lời:

   Hướng dẫn giải

   Đồ thị hàm số đã cho là parabol quay bề lõm lên trên nên hàm số có giá trị nhỏ nhất bằng tung độ đỉnh của parabol.
   Từ đồ thị, ta có đỉnh S có tọa độ (– 1; – 3). Suy ra hàm số có tập giá trị là [– 3; + ∞).
   Quan sát đồ thị ta thấy đồ thị đi xuống từ trái qua phải trên khoảng (– ∞; – 1) nên hàm số nghịch biến trên khoảng (– ∞; – 1) và đồ thị đi lên từ trái qua phải trên khoảng (– 1; + ∞) nên hàm số đồng biến trên khoảng (– 1; + ∞).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm công thức của hàm số có đồ thị vẽ được ở Bài tập 2.
   
   

   Câu hỏi:
   

   Tìm công thức của hàm số có đồ thị vẽ được ở Bài tập 2.

   Trả lời:

   Hướng dẫn giải
   Hàm số bậc hai có công thức tổng quát: y = ax² + bx + c (a ≠ 0).
   Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng – 1 nên c = – 1.
   Hoành độ đỉnh là x_S = – 1 nên \( – \frac{b}{{2a}} = – 1\). Suy ra b = 2a.
   Do đó công thức của hàm số là: y = ax² + 2ax – 1.
   Lại có đồ thị đi qua đỉnh S(– 1; – 3) nên ta có: – 3 = a . (– 1)² + 2a . (– 1) – 1.
   Suy ra a = 2 (t/m) và b = 2 . 2 = 4.
   Vậy hàm số cần tìm là y = 2x² + 4x – 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm công thức hàm số bậc hai biết: Đồ thị hàm số đi qua 3 điểm A(1; – 3), B(0; – 2), C(2; – 10).
   
   

   Câu hỏi:
   

   Tìm công thức hàm số bậc hai biết:
   Đồ thị hàm số đi qua 3 điểm A(1; – 3), B(0; – 2), C(2; – 10).

   Trả lời:

   Hướng dẫn giải
   Hàm số bậc hai có công thức tổng quát: y = ax² + bx + c (a ≠ 0).
   Đồ thị hàm số đi qua điểm A(1; – 3) nên: – 3 = a . 1² + b . 1 + c hay a + b + c = – 3. (1)
   Đồ thị hàm số đi qua điểm B(0; – 2) nên: – 2 = a . 0² + b . 0 + c hay c = – 2.
   Đồ thị hàm số đi qua điểm C(2; – 10) nên: – 10 = a . 2² + b . 2 + c hay 4a + 2b + c = – 10. (2).
   Thay c = – 2 vào (1) ta được: a + b – 2 = – 3 ⇔ a + b = – 1 ⇔ a = – 1 – b. (3)
   Thay c = – 2 vào (2) ta được: 4a + 2b – 2 = – 10 ⇔ 4a + 2b = – 8 ⇔ 2a + b = – 4. (4)
    Thay (3) vào (4) ta được: 2.(– 1 – b) + b = – 4 ⇔ – 2 – 2b + b = – 4 ⇔ b = 2.
   Thay b = 2 vào (3) ta được: a = – 1 – 2 = – 3 (t/m).
   Vậy công thức hàm số là y = – 3x² + 2x – 2.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====