Câu hỏi:
Đội văn nghệ của một trường trung học phổ thông gồm có 5 học sinh khối lớp 10, 5 học sinh khối lớp 11 và 5 học sinh khối lớp 12. Nhà trường cần chọn một đội gồm 10 học sinh để tham gia thi văn nghệ cấp huyện. Tính số cách lập đội văn nghệ sao cho có học sinh ở cả ba khối lớp và có nhiều nhất 2 học sinh khối lớp 10.
Trả lời:
Hướng dẫn giải
Để lập đội văn nghệ gồm 10 học sinh ở cả ba khối và có nhiều nhất 2 học sinh khối lớp 10, ta thấy có 2 trường hợp: đội văn nghệ có đúng 1 học sinh khối lớp 10 và có đúng 2 học sinh khối lớp 10.
– Trường hợp 1: Có đúng 1 học sinh khối lớp 10.
Số cách chọn 1 học sinh khối lớp 10 trong 5 học sinh khối lớp 10 là: \(C_5^1\) cách.
Chọn 9 bạn còn lại ở hai khối lớp 11 và 12, số cách chọn là: \(C_{10}^9\) cách.
Vậy, theo quy tắc nhân, có \(C_5^1.C_{10}^9\) = 5 . 10 = 50 cách lập đội văn nghệ trong trường hợp 1.
– Trường hợp 2: Có đúng 2 học sinh khối lớp 10.
Số cách chọn 2 học sinh khối lớp 10 trong 5 học sinh khối lớp 10 là: \(C_5^2\) cách.
Chọn 8 bạn còn lại ở hai khối lớp 11 và 12, số cách chọn là: \(C_{10}^8\) cách.
Vậy, theo quy tắc nhân, có \(C_5^2.C_{10}^8\) = 10 . 45 = 450 cách lập đội văn nghệ trong trường hợp 2.
Vì hai trường hợp rời nhau nên theo quy tắc cộng, ta có số cách lập đội văn nghệ thỏa mãn yêu cầu của đề bài là: 50 + 450 = 500 (cách).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho các mệnh đề:
P: “Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt”;
Q: “Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0”.
Hãy phát biểu các mệnh đề: P ⇒ Q, Q ⇒ P, P ⇔ Q, . Xét tính đúng sai của các mệnh đề này.
Câu hỏi:
Cho các mệnh đề:
P: “Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt”;
Q: “Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0”.
Hãy phát biểu các mệnh đề: P ⇒ Q, Q ⇒ P, P ⇔ Q, . Xét tính đúng sai của các mệnh đề này.Trả lời:
Hướng dẫn giải
+ Mệnh đề P ⇒ Q: “Nếu phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt thì phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0”. Đây là mệnh đề đúng.
+ Mệnh đề Q ⇒ P: “ Nếu phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0 thì phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt”. Đây là mệnh đề đúng.
+ Mệnh đề P ⇔ Q: “Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt khi và chỉ khi phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0”. Do P ⇒ Q, Q ⇒ P đều là các mệnh đề đúng nên mệnh đề P ⇔ Q là mệnh đề đúng.
+ Mệnh đề
Mệnh đề là mệnh đề phủ định của mệnh đề P và được phát biểu là: “Phương trình bậc hai ax2 + bx + c = 0 không có hai nghiệm phân biệt”.
Mệnh đề là mệnh đề phủ định của mệnh đề Q và được phát biểu là: “Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac ≤ 0”.
Khi đó, ta phát biểu mệnh đề : “Nếu phương trình bậc hai ax2 + bx + c = 0 không có hai nghiệm phân biệt thì phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac ≤ 0”. Mệnh đề này là mệnh đề đúng.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Dùng các khái niệm “điều kiện cần” và “điều kiện đủ” để diễn tả mệnh đề P ⇒ Q.
Câu hỏi:
Dùng các khái niệm “điều kiện cần” và “điều kiện đủ” để diễn tả mệnh đề P ⇒ Q.
Trả lời:
Hướng dẫn giải
+ Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt là điều kiện đủ để phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0.
+ Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0 là điều kiện cần để phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Gọi X là tập hợp các phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt, Y là tập hợp các phương trình bậc hai ax2 + bx + c = 0 có hệ số a và c trái dấu. Nêu mối quan hệ giữa hai tập hợp X và Y.
Câu hỏi:
Gọi X là tập hợp các phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt, Y là tập hợp các phương trình bậc hai ax2 + bx + c = 0 có hệ số a và c trái dấu. Nêu mối quan hệ giữa hai tập hợp X và Y.
Trả lời:
Hướng dẫn giải
Ta có các phương trình bậc hai ax2 + bx + c = 0 có hệ số a và c trái dấu thì luôn có hai nghiệm trái dấu, hiển nhiên đây là hai nghiệm phân biệt. Nhưng các phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt thì hai nghiệm này chưa chắc đã trái dấu.
Do đó mọi phần tử của tập hợp Y thì đều là phần tử của tập hợp X.
Vậy Y là tập con của tập hợp X và ta viết Y ⊂ X.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:
\(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x – 2y \ge – 6}\\{2x + y \le 10}\end{array}} \right.\).
Câu hỏi:
Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:
\(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x – 2y \ge – 6}\\{2x + y \le 10}\end{array}} \right.\).Trả lời:
Hướng dẫn giải
Ta xác định miền nghiệm của từng bất phương trình trong hệ đã cho như sau:
Bước 1: Trục Oy có phương trình x = 0 và điểm (1; 0) thỏa mãn 1 > 0. Do đó miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0) (miền không bị gạch).
Bước 2: Trục Ox có phương trình y = 0 và điểm (0; 1) thỏa mãn 1 > 0. Do đó, miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0; 1) (miền không bị gạch).
Bước 3: Vẽ đường thẳng d1: 3x – 2y = – 6. Lấy điểm O(0; 0) không thuộc d1 và thay x = 0, y = 0 vào biểu thức 3x – 2y ta được: 3 . 0 – 2 . 0 = 0 > – 6. Do đó, miền nghiệm của bất phương trình 3x – 2y ≥ – 6 là nửa mặt phẳng bờ d1 chứa điểm O(0; 0) (miền không bị gạch).
Bước 4: Vẽ đường thẳng d2: 2x + y = 10. Lấy điểm O(0; 0) không thuộc d2 và thay x = 0, y = 0 vào biểu thức 2x + y ta được: 2 . 0 + 0 = 0 < 10. Do đó, miền nghiệm của bất phương trình 2x + y ≤ 10 là nửa mặt phẳng bờ d2 chứa điểm O(0; 0) (miền không bị gạch).
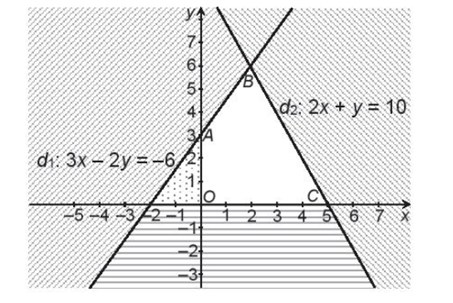
Vậy miền nghiệm D của hệ bất phương trình đã cho là miền tứ giác OABC (miền không bị gạch), trong đó A(0; 3), B(2; 6), C(5; 0), như hình vẽ sau:
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Từ kết quả ở câu a), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D, biết rằng giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D.
Câu hỏi:
Từ kết quả ở câu a), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D, biết rằng giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D.
Trả lời:
Hướng dẫn giải
Vì giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D, do đó ta tính giá trị của F tại (x; y) là tọa độ các đỉnh O, A, B, C.
Ta có: F(0; 0) = 2 . 0 + 3 . 0 = 0;
F(0; 3) = 2 . 0 + 3 . 3 = 9;
F(2; 6) = 2 . 2 + 3 . 6 = 22;
F(5; 0) = 2 . 5 + 3 . 0 = 10.
Vậy giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D lần lượt là 22 và 0.====== **** mời các bạn xem câu tiếp bên dưới **** =====