Có trục đối xứng là x = – 1 và tung độ của đỉnh bằng 5.

Câu hỏi:

Có trục đối xứng là x = – 1 và tung độ của đỉnh bằng 5.

Trả lời:

Lời giải
Parabol có trục đối xứng là x = – 1 ⇔ \(\frac{b}{{2a}} = – 1\) ⇔ b = – 2a (5)
Thay x = – 1 và y = 5 vào parabol y = ax² – bx + 1, ta được:
5 = a.(– 1)² – b.(– 1) + 1 ⇔ a + b = 4 (6).
Từ (5) và (6) ta có hệ phương trình:
\(\left\{ \begin{array}{l}b = 2a\\a + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = – 2a\\a – 2a = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = – 2a\\ – a = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 8\\a = – 4\end{array} \right.\) (thỏa mãn điều kiện).
Vậy parabol cần tìm là: y = – 4x² – 8x + 1.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong các hàm số sau, hàm số nào không là hàm số bậc hai? A. y = – x2 + 4x + 2; B. y = x(2×2 + 5x + 1); C. y = – 3x(6x – 8); D. y = x2 + 6x.
   
   

   Câu hỏi:
   

   Trong các hàm số sau, hàm số nào không là hàm số bậc hai?
   A. y = – x² + 4x + 2;
   B. y = x(2x² + 5x + 1);
   C. y = – 3x(6x – 8);
   D. y = x² + 6x.

   Trả lời:

   Lời giải
   Đáp án đúng là B
   +) Hàm số y = – x² + 4x + 2 có dạng y = ax² + bx + c với a = – 1, b = 4 và c = 2. Do đó A là hàm số bậc hai.
   +) Hàm số y = x(2x² + 5x + 1) = 2x³ + 5x² + x là hàm số bậc 3. Do đó B không là hàm số bậc hai.
   +) Hàm số y = – 3x(6x – 8) = – 18x²  + 24x có dạng y = ax² + bx + c với a = – 18, b = 24 và c = 0. Do đó C là hàm số bậc hai.
   +) Hàm số y = x² + 6x có dạng y = ax² + bx + c với a = 1, b = 6 và c = 0. Do đó C là hàm số bậc hai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số f(x) = 2×2 + 8x + 8. Phát biểu nào sau đây là đúng? A. Hàm số đồng biến trên khoảng (– 4; +∞), nghịch biến trên khoảng (–∞; – 4). B. Hàm số đồng biến trên khoảng (– 2; +∞), nghịch biến trên khoảng (–∞; – 2). C. Hàm số đồng biến trên khoảng (–∞; – 2), nghịch biến trên khoảng (– 2; +∞). D. Hàm số đồng biến trên khoảng (–∞; – 4), nghịch biến trên khoảng (– 4; +∞).
   
   

   Câu hỏi:
   

   Cho hàm số f(x) = 2x² + 8x + 8. Phát biểu nào sau đây là đúng?
   A. Hàm số đồng biến trên khoảng (– 4; +∞), nghịch biến trên khoảng (–∞; – 4).
   B. Hàm số đồng biến trên khoảng (– 2; +∞), nghịch biến trên khoảng (–∞; – 2).
   C. Hàm số đồng biến trên khoảng (–∞; – 2), nghịch biến trên khoảng (– 2; +∞).
   D. Hàm số đồng biến trên khoảng (–∞; – 4), nghịch biến trên khoảng (– 4; +∞).

   Trả lời:

   Lời giải
   Đáp án đúng là B
   Hàm số f(x) = 2x² + 8x + 8 là hàm số bậc hai với a = 2 > 0, ∆ = 8² – 4.2.8 = 0.
   Ta có: \( – \frac{b}{{2a}} = – \frac{8}{{2.2}} = – 2\); \( – \frac{\Delta }{{4a}} = – \frac{0}{{4.2}} = 0\)
   Ta có bảng biến thiên sau:
   
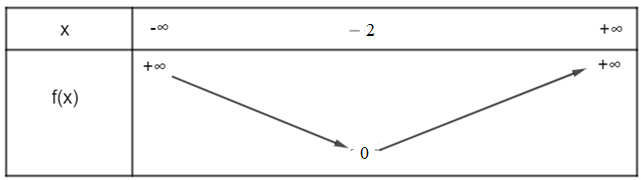
   Vậy hàm số đồng biến trên khoảng (– 2; +∞), nghịch biến trên khoảng (–∞; – 2).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Xác định a, b, c lần lượt là hệ số của x2, hệ số của x và hệ số tự do của các hàm số bậc hai sau: f(x) = x2 – x – 9;
   
   

   Câu hỏi:
   

   Xác định a, b, c lần lượt là hệ số của x², hệ số của x và hệ số tự do của các hàm số bậc hai sau:
   f(x) = x² – x – 9;

   Trả lời:

   Lời giải
   Hàm số f(x) = x² – x – 9 là hàm số bậc hai có a = 1; b = – 1; c = – 9.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. f(x) = x2 – 7;
   
   

   Câu hỏi:
   

   f(x) = x² – 7;

   Trả lời:

   Lời giải
   Hàm số f(x) = x² – 7 = x² + 0x – 7 là hàm số bậc hai có a = 1, b = 0 và c = – 7.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. f(x) = – 2×2 + 8x.
   
   

   Câu hỏi:
   

   f(x) = – 2x² + 8x.

   Trả lời:

   Lời giải
   Hàm số f(x) = – 2x² + 8x = – 2x² + 8x + 0 là hàm số bậc hai có a = – 2, b = 8 và c = 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====