Cho góc α (0° ≤ α ≤ 180°). Trong các khẳng định sau, khẳng định nào sai?

Câu hỏi:

Cho góc α (0° ≤ α ≤ 180°). Trong các khẳng định sau, khẳng định nào sai?

A. sin²α + cos²α = 1;

B. tanα.cotα = 1 (0° < α < 180° và α ≠ 90°);

C. $1+{\tan }^2\alpha =\frac{1}{co{s}^2\alpha }\left(\alpha \ne 90°\right);$ 

D. $1+{\cot }^2\alpha =\frac{1}{co{s}^2\alpha }\left(0°<\alpha <180° và\alpha \ne 90°\right).$ 

Đáp án chính xác

Trả lời:

Hướng dẫn giải
Đáp án đúng là: D
Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho . Gọi (x₀; y₀) là toạ độ điểm M, ta có:
– Tung độ y₀ của M là sin của góc α, kí hiệu là sinα = y₀;
– Hoành độ x₀ của M là côsin của góc α, kí hiệu là cosα = x₀;
– Tỉ số $\frac{y_0}{x_0}$ (x₀ ≠ 0) là tang của góc α, kí hiệu là $\tan \alpha =\frac{y_0}{x_0};$ 
– Tỉ số $\frac{x_0}{y_0}$ (y₀ ≠ 0) là côtang của góc α, kí hiệu là $\cot \alpha =\frac{x_0}{y_0}.$
Gọi H và K lần lượt là hình chiếu của M lên Ox và Oy.

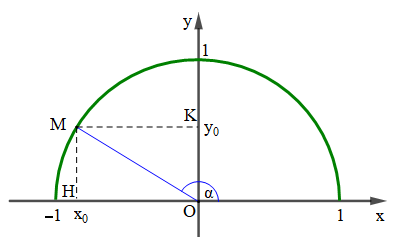
Khi đó ta có: OH = x₀ = cosα, MH = OK = y₀ = sinα, OM = 1.
Tam giác OMH vuông tại H, áp dụng định lí Pythagore ta có:
MH² + OH² = OM²
Hay sin²α + cos²α = 1.
Do đó phương án A là mệnh đề đúng.
Với 0° < α < 180° và α ≠ 90° ta có: $\tan \alpha =\frac{y_0}{x_0};$$\cot \alpha =\frac{x_0}{y_0}.$
$\Rightarrow \tan \alpha .\cot \alpha =\frac{y_0}{x_0}.\frac{x_0}{y_0}=1.$ Do đó phương án B là mệnh đề đúng.
Với α ≠ 90° ta có: $1+{\tan }^2\alpha =1+\frac{{\sin }^2\alpha }{{\text{cos}}^2\alpha }=\frac{{\text{cos}}^2\alpha +{\sin }^2\alpha }{{\text{cos}}^2\alpha }=\frac{1}{co{s}^2\alpha }$ (do sin²α + cos²α = 1).
Do đó phương án C là mệnh đề đúng.
Với 0° < α < 180° và α ≠ 90° ta có:
$1+{\cot }^2\alpha =1+\frac{{\cot }^2\alpha }{{\sin }^2\alpha }=\frac{{\sin }^2\alpha +{\cos }^2\alpha }{{\sin }^2\alpha }=\frac{1}{{\sin }^2\alpha }$(do sin²α + cos²α = 1).
Do đó phương án D là mệnh đề sai.
Vậy ta chọn phương án D.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho α là góc tù. Khẳng định nào sau đây là đúng?
   
   

   Câu hỏi:
   

   Cho α là góc tù. Khẳng định nào sau đây là đúng?

   A. sin α < 0;

   B. cos α > 0;

   C. tan α < 0;

   Đáp án chính xác

   D. cot α > 0.

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: C
   Nếu α là góc tù thì sinα > 0, cosα < 0, tanα < 0, cotα < 0.
   Vậy ta chọn phương án C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 90°. Giá trị của biểu thức P = cosα.cosβ ‒ sinα.sinβ là:
   
   

   Câu hỏi:
   

   Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 90°. Giá trị của biểu thức P = cosα.cosβ ‒ sinα.sinβ là:

   A. P = 0;

   Đáp án chính xác

   B. P = 1;

   C. P = ‒ 1;

   D. P = 2.

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: A
   Hai góc α và β (0° ≤ α, β ≤ 180°) là hai góc phụ nhau (do α + β = 90°) nên sinα = cosβ; cosα = sinβ.
   Do đó, P = cosα.cosβ – sinβ.sinα = cosα. sinα – cosα.sinα = 0.
   Vậy P = 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Trong các đẳng thức sau, đẳng thức nào đúng?
   
   

   Câu hỏi:
   

   Trong các đẳng thức sau, đẳng thức nào đúng?

   A. sin(180° – α) = ‒cos α;

   B. sin(180° – α) = ‒sin α;

   C. sin(180° – α) = sin α;

   Đáp án chính xác

   D. sin(180° – α) = cos α.

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: C
   Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có: sin(180° ‒ α) = sinα.
   Vậy ta chọn phương án C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:
   
   

   Câu hỏi:
   

   Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:

   A. ‒1

   B. 0

   Đáp án chính xác

   C. 1

   D. 2

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Xét tam giác ABC ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong tam giác)
   $\Rightarrow \widehat{B}+\widehat{C}=180°-\widehat{A}$ 
   Þ cos(B + C) = cos(180° ‒ A) = ‒cosA;
   Và sin(B + C) = sin(180° ‒ A)= sinA.
   Do đó:
   sinA.cos(B + C) + cosA.sin(B + C)
   = sinA.(‒cosA) + cosA.sinA
   = ‒sinA.cosA + cosA.sinA
   = 0
   Vậy sinA.cos(B + C) + cosA.sin(B + C) = 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Giá trị cos135° + sin135° bằng bao nhiêu?
   
   

   Câu hỏi:
   

   Giá trị cos135° + sin135° bằng bao nhiêu?

   A. $\sqrt{3};$ 

   B. 0

   Đáp án chính xác

   C. 1

   D. $\sqrt{2}$ 

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Ta có: $cos135°=-\frac{\sqrt{2}}{2};\sin 135°=\frac{\sqrt{2}}{2};$ 
   Do đó: cos135° + sin135° $=-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}=0$ 
   Vậy cos135° + sin135° = 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====